реферати. Задачи_резервирование. Вероятность безотказной работы системы при раздельном дублировании и равнонадежных элементах равна
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
1. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента ср =10000Т ч. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти среднее время безотказной работы системы Cр =1000Т , а также частоту отказов с t и интенсивность отказов с t в момент времени t = 50 ч в следующих случаях: а) нерезервированной системы, б) дублированной системы при постоянно включенном резерве. Ответ:  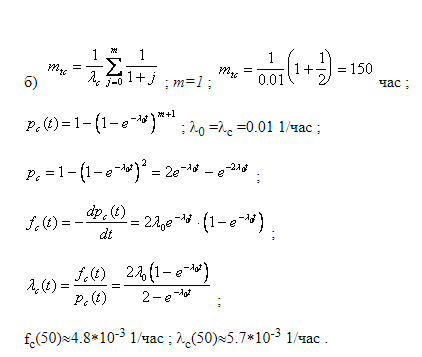 2. Нерезервированная система управления состоит из n=5000 элементов. Для повышения надежности системы предполагается провести общее дублирование элементов. Чтобы приближенно оценить возможность достижения заданной вероятности безотказной работы системы Рс(t) = 0,9 при t =10 ч, необходимо рассчитать среднюю интенсивность отказов одного элемента при предположении отсутствия последействия отказов. Ответ Вероятность безотказной работы системы при раздельном дублировании и равнонадежных элементах равна:  3. Вероятность безотказной работы преобразователя постоянного тока в переменный в течение времени t=1000 ч равна 0,95, т. е. Р(1000) = 0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включается в работу при отказе первого (режим ненагруженного резерва). Требуется рассчитать вероятность безотказной работы и среднее время безотказной работы системы, состоящей из двух преобразователей, а также определить частоту отказов с t и интенсивность отказов с t системы Ответ В рассматриваемом случае кратность резервирования m = 1. Используя формулу (5.9), получим   4. Основная функционально-необходимая система представляет собой последовательное (в смысле надежности) соединение элементов. Число элементов n = 4. Интенсивность отказов у каждого из элементов равна = 0,210–3 . Определить показатели надежности системы без резервирования и при различных методах резервирования на момент времени 1000 час, при кратности резервирования m = 1, m = 2. Сравнить эффективность методов резервирования. Ответ     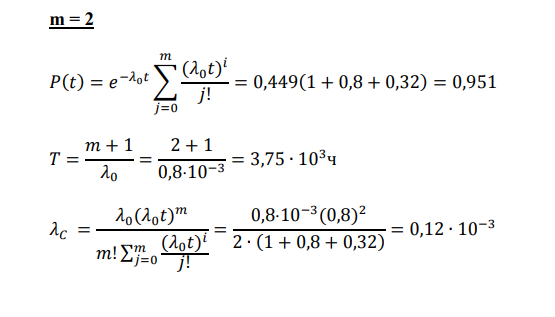 . . Основная функционально-необходимая система представляет собой последовательное (в смысле надежности) соединение элементов. Число элементов n = 4. Интенсивность отказов у каждого из элементов равна = 0,210–3 . Определить показатели надежности системы без резервирования и при различных методах резервирования на момент времени 1000 час, при кратности резервирования m = 1, m = 2. Сравнить эффективность методов резервирования. Ответ 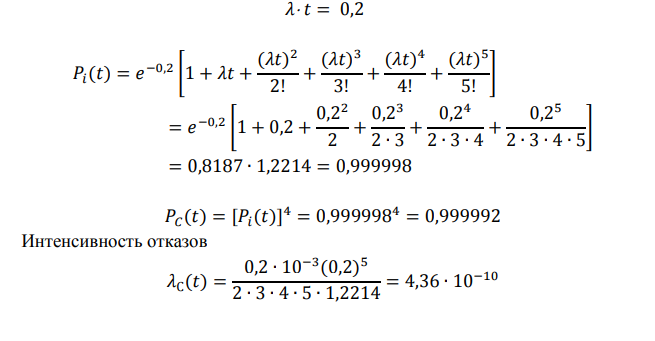 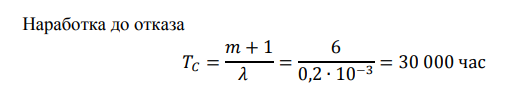 5. Система имеет кратность раздельного резервирования замещением с целой кратностью m = 5. Основная нерезервированная система содержит четыре равнонадежных элемента с логически последовательным соединением. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч Ответ Определим интенсивность отказов основной системы по формуле  6. Система построена из 4 однотипных блоков, которые имеют интенсивность отказов λ = 0,210-3 . Определить показатели надежности системы за 1000 час работы, если в скользящем «холодном» резерве находится: 1 такой же блок, 2 таких же блока. Резервные блоки могут заменить в случае отказа любой из отказавших блоков Ответ   7. Система имеет общее резервирование с дробной кратностью и постоянно включенным резервом. Система работоспособна, если работоспособны не менее 2-х элементов из 3-х. Определить показатели надежности для t = 1000 час, если интенсивность отказов элементов λ = 0,210- 3 . Ответ:  8. Система имеет кратность общего резервирования m = 5. Основная нерезирвированная система содержит четыре равнонадежных элемента с логически последовательным соединением. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч Ответ   9. Определить характеристики надежности системы при кратности раздельного резервирования каждого элемента m = 5. Интенсивность отказов одного элемента λ = 0,210-3 . Определить характеристики надежности системы за 1000 ч. Ответ     10. Найти среднюю наработку до первого отказа и вероятность безотказной работы устройства, структурная схема которого приведена на рис При его двукратном резервировании, если р1 = 0,9; p2 = 0,7; tраб = 100 ч Ответ. 1. Необходимо найти вероятность безотказной работы устройства без резервирования,  для этого определим вероятность безотказной работы каждой ветви устройства      Вероятность безотказной работы при двукратном резервировании такими же устройствами будет равна   2.Средняя наработка до первого отказа при двукратном резервировании будет определятся по следующей формуле, час,  Среднее время безотказной работы нерезервируемой системы, час,     . . Ответ:   |
