Выбор формы уравнения регрессии

• Название: Выбор формы уравнения регрессии
• Анкор: kira_shpory.doc
• Дата: 07.05.2018
• Размер: 8.7 Mb.
• Имя файла: kira_shpory.doc
• Тип: Документы; #19000
• страница: 10 из 13

36. Функция правдоподобия в математической статистике - это совместное распределение выборки из параметрического распределения как функция параметра.

Определение

Пусть есть параметрическое семейство распределений вероятности . Пусть дана выборка для некоторого . Предположим, что совместное распределение этой выборки задаётся функцией , где f является либо плотностью вероятности, либо функцией вероятности случайного вектора .

Для фиксированной реализации выборки функция называется функцией правдоподобия.

Замечания

Функция , где

,

называется логарифмической функцией правдоподобия.

Если выборка независима, то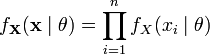

,

где - плотность или функция вероятности распределения . Логарифмическая функция правдоподобия в этом случае имеет вид: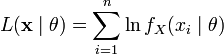

.

Функция правдоподобия измеряет степень вероятности появления реализации выборки из распределения .

37. Метод Бокса-Кокса

Для исходной последовательности X длиной N



Однопараметрическое Бокс-Кокс преобразование определяется следующим образом: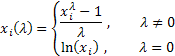



где .

Как видим, это преобразование имеет единственный параметр - лямбда. При значении лямбда равном нулю осуществляется логарифмическое преобразование входной последовательности, при значении лямбда отличном от нуля – степенное. Если параметр лямбда равен единице, то закон распределения исходной последовательности не изменяется, хотя при этом последовательность получит сдвиг за счет вычитания единицы из каждого ее значения.

В зависимости от значения лямбда, преобразование Бокса-Кокса включает в себя следующие частные случаи: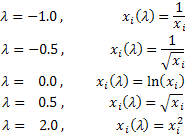



При использовании Бокс-Кокс преобразования необходимо, чтобы все значения входной последовательности были положительными и отличными от нуля. Если входная последовательность не удовлетворяет этим требованиям, то ее можно сдвинуть в положительную область на величину, гарантирующую "положительность" всех ее значений.

Остановимся пока на рассмотрении только однопараметрического Бокс-Кокс преобразования, подготавливая для него соответствующим образом входные данные. Для того, чтобы избежать во входных данных появления отрицательных или равных нулю значений, всегда будем находить минимальное значение входной последовательности и вычитать его из каждого ее элемента, дополнительно осуществляя сдвиг на небольшую величину, равную 1e-5. Такое дополнительное смещение необходимо для гарантированного сдвига последовательности в положительную область, в случае, если минимальное ее значение равно нулю.

Для последовательностей, которые содержат только положительные значения, такого сдвига можно было бы и не делать, но для того чтобы в процессе преобразования при возведении в степень снизить вероятность получения излишне больших величин, и для "положительных" последовательностей будем использовать тот же алгоритм сдвига. Таким образом, любая входная последовательность после сдвига будет располагаться в положительной области, и иметь при этом близкое к нулю минимальное значение.

На рис. 1 показано, как выглядят кривые Бокс-Кокс преобразования при различных значениях параметра лямбда. Рис. 1 заимствован из статьи "Box-Cox Transformations" [3]. Горизонтальная шкала на графике представлена в логарифмическом масштабе.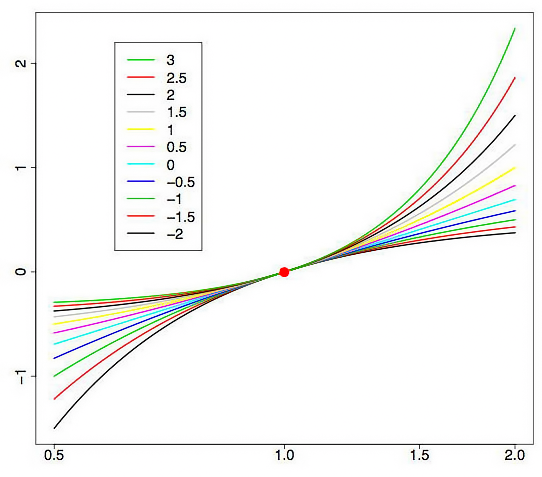



Рис. 1. Бокс-Кокс преобразование при различных значениях параметра лямбда

Как видим, при изменении параметра лямбда "хвосты" исходного распределения могут быть или "растянуты", или "поджаты". Верхняя кривая на рис. 1 соответствует значению лямбда=3, а нижняя значению лямбда=-2.

Для того чтобы в результате Бокс-Кокс преобразования закон распределения результирующий последовательности был максимально приближен к нормальному закону, необходимо выбрать оптимальное значение параметра лямбда.

Одним из способов определения оптимальной величины этого параметра является максимизация логарифма функции правдоподобия:



где



То есть необходимо выбрать такое значение параметра лямбда, при котором данная функция принимает максимальное значение.

В публикации "Box-Cox Transformations" [3] кратко рассматривается другой способ определения оптимального значения этого параметра, основанный на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью. Наверняка можно найти и другие методы оптимизации параметра лямбда, но для начала остановим свой выбор на поиске максимума логарифма приведенной ранее функции правдоподобия.

Находить максимум логарифма функции правдоподобия можно разными способами. Например, методом простого перебора. Для этого необходимо в выбранном диапазоне, изменяя с небольшим шагом величину параметра лямбда, вычислять значение функции правдоподобия. И в качестве оптимального значения лямбда выбрать то, при котором величина функции правдоподобия окажется максимальной. 

При этом величина шага будет определять точность вычисления оптимального значения параметра лямбда. Чем мельче шаг, тем выше точность, но при уменьшении шага пропорционально будет увеличиваться и требуемый объем вычислений. Для повышения эффективности вычислений могут быть использованы различные алгоритмы поиска максимума/минимума функции, генетические алгоритмы и так далее.

38. Коэффициент ранговой корреляции Спирмена.

Если потребуется установить связь между двумя признаками, значения которых в генеральной совокупности распределены не по нормальному закону, т. е. предположение о том, что двумерная выборка (xi и yi) получена из двумерной нормальной генеральной совокупности, не принимается, то можно воспользоваться коэффициентом ранговой корреляции Спирмена ():



где dx и dy – ранги показателей xi и yi; n – число коррелируемых пар.

Коэффициент ранговой корреляции также имеет пределы 1 и –1. Если ранги одинаковы для всех значений xi и yi, то все разности рангов (dx - dy) = 0 и = 1. Если ранги xi и yi расположены в обратном порядке, то = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений x_i и y_i.

Когда ранги всех значений x_i и y_i строго совпадают или расположены в обратном порядке, между случайными величинами Х и Y существует функциональная зависимость, причем эта зависимость не обязательно линейная, как в случае с коэффициентом линейной корреляции Браве-Пирсона, а может быть любой монотонной зависимостью (т. е. постоянно возрастающей или постоянно убывающей зависимостью). Если зависимость монотонно возрастающая, то ранги значений x_i и y_i совпадают и = 1; если зависимость монотонно убывающая, то ранги обратны и = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y.

Из формулы видно, что для вычисления необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)². Зная эти значения, находятся суммы , учитывая, что всегда равна нулю. Затем, вычислив значение , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если , то между признаками наблюдается недостоверная корреляционная взаимосвязь.

Коэффициент ранговой корреляции Спирмена вычисляется значительно проще, чем коэффициент корреляции Браве-Пирсона при одних и тех же исходных данных, поскольку при вычислении используются ранги, представляющие собой обычно целые числа.

Коэффициент ранговой корреляции целесообразно использовать в следующих случаях:

- если экспериментальные данные представляют собой точно измеренные значения признаков Х и Y и требуется быстро найти приближенную оценку коэффициента корреляции. Тогда даже в случае двумерного нормального распределения генеральной совокупности можно воспользоваться коэффициентом ранговой корреляции вместо точного коэффициента корреляции Браве-Пирсона. Вычисления будут существенно проще, а точность оценки генерального параметра р с помощью коэффициента при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций;

- когда значения x_i и (или) y_i заданы в порядковой шкале (например, оценки судей в баллах, места на соревнованиях, количественные градации качественных признаков), т. е. когда признаки не могут быть точно измерены, но их наблюдаемые значения могут быть расставлены в определенном порядке.

39. Коэффициенты эластичности

Коэффициенты регрессии нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х. 

Для этих целей вычисляются коэффициенты эластичности.

Коэффициент эластичности рассчитывается по следующей формуле:







40. фиктивные переменные

Термин “фиктивные переменные” используется как противоположность “значащим” пе­ременным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная пе­ременная, отражающая качественную характеристику. Это могут быть разного рода атрибутивные призна­ки, такие, например, как профессия, пол, образование, климати­ческие условия, принадлежность к определенному региону. Что­бы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. каче­ственные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принятоназывать фиктивными переменными. В литературе можно встретить термины «структурные переменные» или «искусственные переменные»
Например, в результате опроса группы людей 0 может означать, что опра­шиваемый — мужчина, а 1 — женщина. К фиктивным переменным иногда относят рег­рессор, состоящий из одних единиц (т.е. константу, свободный член), а также временной тренд.
Фиктивные переменные позволяют строить и оценивать кусочно-линейные модели, которые можно применять для исследования структурных изменений. 
Пусть, например, мы исследуем зависимость выпуска продукции Y от размера основного фонда предприятия хt. При этом есть основания считать, что в момент времени t₀произошла структурная перестройка и характер зависимости изменился.
Чтобы оценить такую модель введем бинарную переменную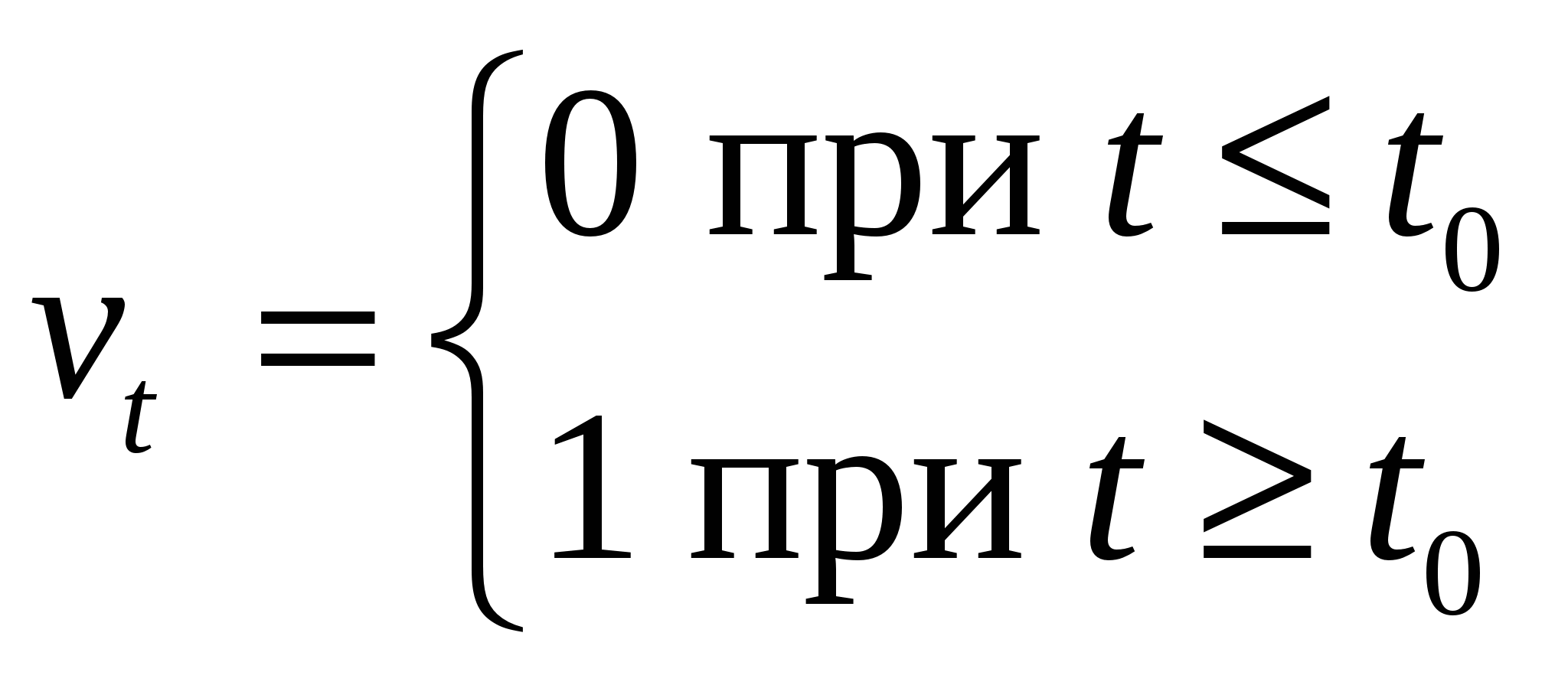


и запишем нашу модель в виде: 

При t ≤ t₀ линия регрессии имеет наклон , при t > t₀наклон равен и разрыва в точке x_tне происходит. При  приходим к выводу, что в момент t0 структурного изменения не происходит.

 Использование фиктивных переменных в моделях с временными рядами
В регрессионных моделях с временными рядами используется три основных вида фиктивных переменных:
1) Переменные-индикаторы принадлежности наблюдения к определенному периоду — для моделирования скачкообразных структурных сдвигов. Границы периода (моменты “скачков”) должны быть установлены из априорных соображений. Например, 1, если наблюдение принадлежит периоду 1941-45 гг. и 0 в противном случае. Это пример использования для моделирования временного структурного сдвига. Постоянный структурный сдвиг моделируется переменной равной 0 до определенного момента времени и 1 для всех наблюдений после этого момента времени.
2) Сезонные переменные — для моделирования сезонности. Сезонные переменные принимают разные значения в зависимости от того, какому месяцу или кварталу года или какому дню недели соответствует наблюдение.
Например,модель потребления, учитывающая сезонные колебания.
у = b₀ + b1x1 + b₂x₂ + b₃x₃,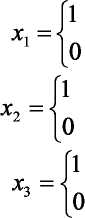

для зимних месяцев 
иначе
для весенних месяцев
иначе
для летних месяцев
иначе
Следует отметить, что вводить четвертую переменную х₄для осенних месяцев не требуется, т.к. в этом случае все переменные оказались бы связанными тождеством
Xi +Х₂+Хз+Х₄= 1,
что привело бы их к полной коллинеарности и вырожденности информационной матрицы .
Для осенних месяцев коэффициенты b1, b₂, b3 равны нулю и объем потребления составляет Y= b0
Для зимних месяцев: Y=b0 + b1,
Для весенних месяцев: Y=b0 + b₂,
Для летних месяцев: Y=b0 + b3.
При этом, если в результате регрессионного анализа окажется, что b3 = 0, это означает, что между летними и осенними сезонами различие в потреблении несущественно. При b1 = b₂отсутствует различие между потреблением зимой и весной и т.д.
3) Линейный временной тренд — для моделирования постепенных плавных структурных сдвигов. Эта фиктивная переменная показывает, какой промежуток времени прошел от некоторого “нулевого” момента времени до того момента, к которому относится данное наблюдение (координаты данного наблюдения на временной шкале). Если промежутки времени между последовательными наблюдениями одинаковы, то временной тренд можно составить из номеров наблюдений.
Временной тренд отличается от бинарных фиктивных переменных тем, что имеет смысл использовать его степени: t² , t³ и т. д. Они помогают моделировать гладкий, но нелинейный тренд. (Бинарную переменную нет смысла возводить в степень, потому что в результате получится та же самая переменная.)
Можно также комбинировать указанные виды фиктивных переменных, создавая переменные “взаимодействия” соответствующих эффектов.
Комбинация рассмотренных фиктивных переменных позволяет моделировать еще один эффект — изменение наклона тренда с определенного момента. Помимо тренда в регрессию следует тогда ввести следующую переменную: в начале выборки до некоторого момента времени она равна 0, а вторая ее часть представляет собой временной тренд (1, 2, 3 и т. д. в случае одинаковых интервалов между наблюдениями).
Использование фиктивных переменных имеет следующие преимущества:
Интервалы между наблюдениями не обязательно должны быть одинаковыми. В выборке могут быть пропущенные наблюдения.

Коэффициенты при фиктивных переменных легко интерпретировать, они наглядно представляют структуру динамического процесса.

Для оценивания модели не приходится выходить за рамки классического метода наименьших квадратов.