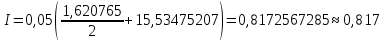эвм. лб. Вычисление интеграла функции по формулам прямоугольников (левых,правых, средних)
 Скачать 105.77 Kb. Скачать 105.77 Kb.
|
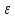 , необходимо определить значение , необходимо определить значение 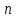 (количество частей на которое следует разделить отрезок предела интегрирования ), так чтобы выполнялось неравенство (количество частей на которое следует разделить отрезок предела интегрирования ), так чтобы выполнялось неравенство 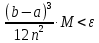 , где где a- нижний предел интегрирования, b- верхний предел интегрирования, , где где a- нижний предел интегрирования, b- верхний предел интегрирования, 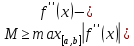 вторая производная от подынтегральной функции). вторая производная от подынтегральной функции).После нахождения 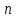 , находим шаг , находим шаг  . .Найти точки деления отрезка предела интегрирования функции 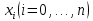 и значения подынтегральной функции и значения подынтегральной функции  в точках в точках 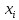 . .Вычислить значение интеграла  по формуле по формуле 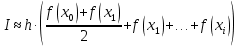 , где , где 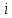 , значение от нуля до , значение от нуля до 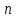 . .Пример. Вычислить интеграл по формуле трапеций. 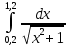 Для достижения заданной степени точности необходимо определить значение 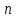 , так ,чтобы , так ,чтобы 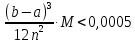 Здесь 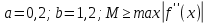 , где , где 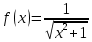 . Находим . Находим 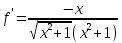 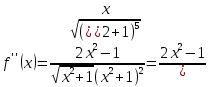 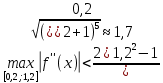 Положим 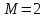 , тогда неравенство примет вид , тогда неравенство примет вид 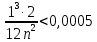 , откуда , откуда  , т.е. , т.е. 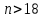 . Возьмем . Возьмем 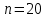 Вычисление интеграла производим по формуле 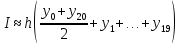 , где , где 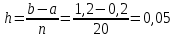 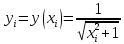 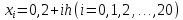
Вычисление интеграла функции по формуле Симпсона . Методика решения задачи Разбить отрезок предела интегрирования на равное количество n частей с шагом  , где a- нижний предел интегрирования, b- верхний предел интегрирования. , где a- нижний предел интегрирования, b- верхний предел интегрирования.Найти точки деления отрезка предела интегрирования функции 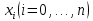 и значения подынтегральной функции и значения подынтегральной функции  в точках в точках 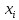 . .Вычислить значение интеграла  по формуле по формуле 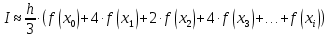 , где , где 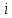 , значение от нуля до , значение от нуля до 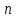 . .Пример. Вычислить интеграл по формуле Симпсона при 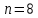 . Оценить погрешность результата, составив таблицу конечных разностей. . Оценить погрешность результата, составив таблицу конечных разностей. 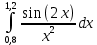 Согласно условию 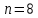 , поэтому , поэтому 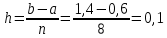 Вычислительная формула имеет вид 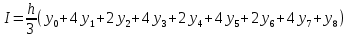 , где , где 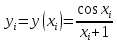 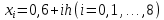 Вычисление значений функции, а также сложение значений функции, имеющих одинаковые коэффициенты в формуле, производим в таблице.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||