эвм. лб. Вычисление интеграла функции по формулам прямоугольников (левых,правых, средних)
 Скачать 105.77 Kb. Скачать 105.77 Kb.
|
 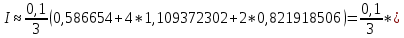 6,66798 6,66798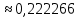 | ||||||||||||
| i | y(i) | ∆y(i) | ∆²y(i) | ∆³y(i) | 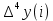 |
| 0 | 0,515835 | -0,06593 | 0,00308 | -0,00012796 | 0,000060369 |
| 1 | 0,449907 | -0,06285 | 0,002952 | -0,000067591 | 0,000042426 |
| 2 | 0,387059 | -0,0599 | 0,002884 | -0,000025165 | 0,000029094 |
| 3 | 0,327163 | -0,05701 | 0,002859 | 0,000003929 | 0,000019005 |
| 4 | 0,270151 | -0,05415 | 0,002863 | 0,000022934 | 0,000011251 |
| 5 | 0,215998 | -0,05129 | 0,002886 | 0,000034185 | |
| 6 | 0,164708 | -0,0484 | 0,00292 | | |
| 7 | 0,116304 | -0,04548 | | | |
| 8 | 0,07082 | | | | |
| max│∆^4y(i)│ | 0,000060369 |
| R(ост) | 0,000000268 |
Вычисления производились с девятью значащими цифрами, а потому величина остаточного члена влияет на погрешность .
Вычисление интеграла функции по формуле «трех восьмых»
Методика решения задачи.
Разбить отрезок предела интегрирования на равное количество n частей с шагом
 , где a- нижний предел интегрирования, b- верхний предел интегрирования.
, где a- нижний предел интегрирования, b- верхний предел интегрирования.Найти точки деления отрезка предела интегрирования функции
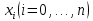 и значения подынтегральной функции
и значения подынтегральной функции  в точках
в точках 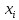 .
.Вычислить значение интеграла
 по формуле
по формуле 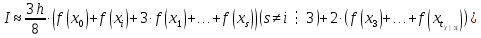 , где
, где 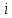 , значение от нуля до
, значение от нуля до 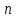 ,
, 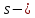 значения от 1 до
значения от 1 до 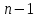 не кратные трем, t- значения от 1 до
не кратные трем, t- значения от 1 до 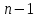 кратные трем.
кратные трем.Пример.
Найти приближенное значение интеграла по формуле «трех восьмых» используя для контроля точности вычислений двойной просчет при
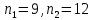
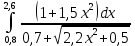
Воспользуемся формулой «трех восьмых» выражающей данный интеграл через суммы значений подынтегральной функции
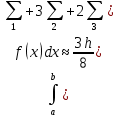
где
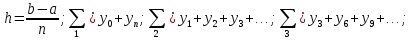
число разбиений должно быть кратным трем.
| i | x(i) | 1+1,5x^2 | 0,7+√(2,2x^2+0,5) | y(0),y(9) | y(1,2,4,5,7,8) | y(3,6) | | |||||
| 0 | 0,8 | 1,96 | 2,081303732 | 0,941717 | | | | |||||
| 1 | 1 | 2,5 | 2,343167673 | | 1,06693176 | | | |||||
| 2 | 1,2 | 3,16 | 2,615202339 | | 1,20831951 | | | |||||
| 3 | 1,4 | 3,94 | 2,893627133 | | | 1,361613 | | |||||
| 4 | 1,6 | 4,84 | 3,176287544 | | 1,52379151 | | | |||||
| 5 | 1,8 | 5,86 | 3,461883415 | | 1,6927202 | | | |||||
| 6 | 2 | 7 | 3,749590136 | | | 1,866871 | | |||||
| 7 | 2,2 | 8,26 | 4,038862082 | | 2,04513049 | | | |||||
| 8 | 2,4 | 9,64 | 4,329325006 | | 2,22667506 | | | |||||
| 9 | 2,6 | 11,14 | 4,620714221 | 2,410883 | | | | |||||
| сумма |
| | | 3,3526 | 9,76356853 | 3,228484 | | |||||
| | | | ||||||||||
| | | |||||||||||
| |  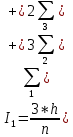 | | ||||||||||
| | | |||||||||||
| |  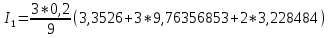 =2,606685 =2,606685 | | | | | | | |||||
| i | x(i) | 1+1,5x^2 | 0,7+√(2,2x^2+0,5) | y(0),y(12) | y(1,2,4,5,7,8,10,11) | y(3,6,9) | | |||||
| 0 | 0,8 | 1,96 | 2,081303732 | 0,941717 | | | | |||||
| 1 | 0,95 | 2,35375 | 2,276546859 | | 1,03391239 | | | |||||
| 2 | 1,1 | 2,815 | 2,478201338 | | 1,13590448 | | | |||||
| 3 | 1,25 | 3,34375 | 2,684313483 | | | 1,245663 | | |||||
| 4 | 1,4 | 3,94 | 2,893627133 | | 1,36161289 | | | |||||
| 5 | 1,55 | 4,60375 | 3,105306633 | | 1,4825428 | | | |||||
| 6 | 1,7 | 5,335 | 3,318778341 | | | 1,607519 | | |||||
| 7 | 1,85 | 6,13375 | 3,533637239 | | 1,73581768 | | | |||||
| 8 | 2 | 7 | 3,749590136 | | 1,86687071 | | | |||||
| 9 | 2,15 | 7,93375 | 3,966420059 | | | 2,000229 | | |||||
| 10 | 2,3 | 8,935 | 4,18396326 | | 2,135535 | | | |||||
| 11 | 2,45 | 10,00375 | 4,402094002 | | 2,27249804 | | | |||||
| 12 | 2,6 | 11,14 | 4,620714221 | 2,410883 | | | | |||||
| сумма | | | | 3,3526 | 13,024694 | 4,853412 | | |||||
| |
| | | | | | | |||||
| | | |||||||||||
