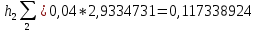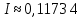Для решения воспользуемся формулой средних прямоугольников .

Вычисления выполним дважды при 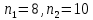 и соответственно при и соответственно при  и и 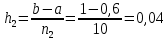 . Результаты вычислений приведены в таблицах . Результаты вычислений приведены в таблицах
i
|
x(i)
|
x(i)+h/2
|
cos(0,6*x^2+0,4)
|
1,4+(sin(x+0,7))^2
|
y(x(i)+h/2)
|
|
|
|
0
|
0,6
|
0,625
|
0,805442275
|
2,340791098
|
0,3440898
|
|
|
|
1
|
0,65
|
0,675
|
0,781721378
|
2,362151189
|
0,3309362
|
|
|
|
2
|
0,7
|
0,725
|
0,754847332
|
2,378893619
|
0,3173103
|
|
|
|
3
|
0,75
|
0,775
|
0,724577614
|
2,390851101
|
0,3030626
|
|
|
|
4
|
0,8
|
0,825
|
0,690674489
|
2,397904162
|
0,2880326
|
|
|
|
5
|
0,85
|
0,875
|
0,652910992
|
2,399982329
|
0,2720482
|
|
|
|
6
|
0,9
|
0,925
|
0,611077684
|
2,397064838
|
0,2549275
|
|
|
|
7
|
0,95
|
0,975
|
0,564990159
|
2,389180839
|
0,2364786
|
|
|
|
сумма
|
|
|
|
|
2,3468858
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i
|
x(i)
|
x(i)+h/2
|
cos(0,6*x^2+0,4)
|
1,4+(sin(x+0,7))^2
|
y(x(i)+h/2)
|
|
|
|
0
|
0,6
|
0,62
|
0,80765029
|
2,338408945
|
0,3453845
|
|
|
|
1
|
0,64
|
0,66
|
0,789157662
|
2,356219181
|
0,3349254
|
|
|
|
2
|
0,68
|
0,7
|
0,768693703
|
2,37111117
|
0,3241913
|
|
|
|
3
|
0,72
|
0,74
|
0,746133922
|
2,382989656
|
0,3131083
|
|
|
|
4
|
0,76
|
0,78
|
0,721354655
|
2,391778657
|
0,3015976
|
|
|
|
5
|
0,8
|
0,82
|
0,694234887
|
2,397421952
|
0,2895756
|
|
|
|
6
|
0,84
|
0,86
|
0,664658256
|
2,399883444
|
0,2769544
|
|
|
|
7
|
0,88
|
0,9
|
0,63251527
|
2,399147388
|
0,2636417
|
|
|
|
8
|
0,92
|
0,94
|
0,597705715
|
2,395218492
|
0,2495412
|
|
|
|
9
|
0,96
|
0,98
|
0,560141272
|
2,388121888
|
0,234553
|
|
|
|
сумма
|
|
|
|
|
2,9334731
|
|
|
|
|
|
|
|
|
|
|
|
|
найдем приближенные значения интеграла
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

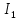 = =
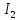 = =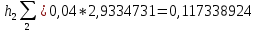
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

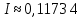
значения различаются в десятичных долях , но первое значение точнее второго , поэтому принимаем
|
|
Вычисление интеграла функции по формуле трапеций
Методика решения задачи.
Для достижения заданной степени точности |
 Скачать 105.77 Kb.
Скачать 105.77 Kb.
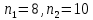 и соответственно при
и соответственно при  и
и 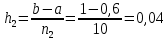 . Результаты вычислений приведены в таблицах
. Результаты вычислений приведены в таблицах 

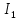 =
=
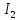 =
=