Практическая работа расчет погрешности. ПР 1 расчет погрешности. Вычисление погрешностей средств измерений
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Практическая работа Тема: «Вычисление погрешностей средств измерений» Цель работы: определить погрешности измерения при заданных параметрах. студент должен: ЗНАТЬ: понятие погрешности измерений и их характеристики; УМЕТЬ: рассчитать характеристики погрешности измерения. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ: Погрешностьюназывается отклонение результата измерения от истинного значения измеряемой величины. В электротехнических измерениях различают несколько видов погрешностей, которые можно объединить в две большие группы: основная и дополнительная. Основная погрешностьопределяется при нормальных условиях работы: температуре, влажности окружающей среды, частоте, форме и значение питающего напряжения, рабочем положении (для электромеханических приборов), Дополнительная погрешностьпоявляется при отклонении величин, влияющих на результат измерения, от нормальных. Нормальными условиями работы для измерительных приборов являются следующие: температура (20 ± 5) °С; относительная влажность (60 ± 15)%; атмосферное давление (750 ± 30) мм рт.ст.; при питании от сети переменного тока значение напряжения может отличаться от нормального (номинального) значения не более чем на ±10%, т.е. сетевое напряжение 220 В может колебаться в диапазоне 198...242 В,а его частота —не более чем на + 1 Гц, т.е.в диапазоне 49...51 Гц. Основная погрешность содержит две составляющие — систематическую и случайную. Систематическая погрешностьпри повторных измерениях одной и той же величины одним и тем же прибором остается постоянной или изменяется по определенному закону. В обоих случаях она легко обнаруживается и может быть исключена из результата измерений. Основными способами уменьшения систематической погрешности являются предварительная установка показаний индикатора на нуль, предварительная калибровка прибора и введение поправки. Предварительная (перед измерением) установка показаний индикатора на нуль в аналоговых электромеханических и электронных приборах осуществляется механическим корректором, выведеннымпод шлиц в нижней части стрелочного индикатора, при выключенном приборе; в цифровых и аналоговых электронных приборах — специальным регулировочным потенциометром, выведенным на лицевую панель прибора и обозначенным символом Предварительная (перед измерением) калибровка прибора выполняется только для электронных приборов регулировочным потенциометром, чаще всего выведенным на лицевую панель и обозначенным символом «▼» (или «Калибр»), при включенном приборе. О введении поправки речь будет идти ниже. Случайная погрешность при повторных измерениях изменяется случайным образом. Она резко выделяется на фоне систематической погрешности и возникает часто в результате оплошности оператора (ошибочного отсчета и записи показаний, влияния природных или техногенных воздействий). Основным способом уменьшения случайной погрешности является обработка результатов измерений методом статистики и теории вероятности. Одним из признаков, по которым классифицируются измерения, является способ получения результата измерения. Измерения подразделяются на прямые и косвенные. При прямых измерениях искомая величина определяется непосредственно. Например, ток — амперметром, напряжение — вольтметром. При косвенных измерениях результат находится путем выполнения определенных математических действий над результатами измерений. Например, измерение частоты осциллографом. Будущему специалисту со средним профессиональным образованием необходимо научиться быстро, уверенно и правильно оценивать наиболее часто встречающиеся погрешности измерения. Поэтому далее рассмотрим количественную оценку основной систематической погрешности при прямых и косвенных измерениях. Для количественной оценки основной систематической погрешности при прямых измерениях пользуются формулами, выражающими абсолютную, действительную относительную и приведенную относительную погрешности измерения. Абсолютная погрешность ∆ выражается как ∆=Аи-Ад (1.1) где Аи— истинное значение измеряемой величины (с определенным допуском будем считать его показанием образцового прибора); Ад— измеренное, действительное значение величины (показание рабочего прибора). Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, мА, В; Вт и т.п.). Абсолютная погрешность не дает представления о точности измерения, поэтому используют действительную относительную погрешность γд Действительная относительная погрешность γд выражается как γд = ±(∆/ Ад)*100% (1.2) Приведенная относительная погрешность γпр выражается как γпр=± (∆мах/ Хn) *100% (1.3) где ∆мах — максимальная абсолютная погрешность; Хn — нормируемое значение, которое зависит от типа шкалы: -если шкала односторонняя и нижний предел измерения равен нулю (например, шкала прибора от 0 до 150 В), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 В). -если шкала односторонняя, но нижний предел измерения не равен нулю (например, шкала прибора от 30 до 150 В), то Хn принимается равным разности верхнего и нижнего пределов измерения Хn = Хмах-Хмин (в нашем случае Хn = 150-30 = 120 В). -если шкала прибора двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С). Приведенная относительная погрешность γпр характеризует класс точности прибора (К). Приведенная погрешность выражается в процентах, либо является безразмерной величиной. Проанализировав формулы (1.2) и (1.3), построим графики зависимости γд и γпр от показания измерительного прибора (положения стрелки) на примере односторонней шкалы прибора (рис. 1). Поделив шкалу прибора на четыре равные части от нуля до Хn можно утверждать, что γд максимальна в 1-й четверти шкалы и минимальна в 4-й четверти. 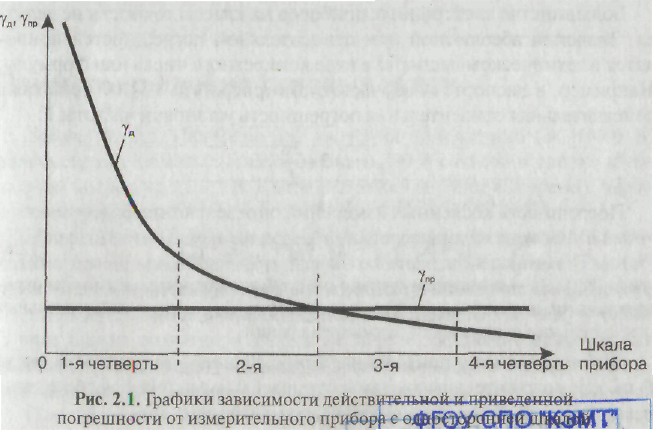 Рисунок 1 – График зависимости действительной и приведенной погрешности от измерительного прибора На основании анализа зависимостей можно сделать следующие выводы. Для получения наименьшей погрешности γд необходимо использовать 4-ю или 3-ю четверть шкалы прибора и не измерять в других четвертях, так как в 1-й и 2-й четверти шкалы погрешность максимальна. Из анализа графика зависимости γпр=f(Ад) следует, что приведенная относительная погрешность не зависит от показания прибора. Поэтому, действительная относительная погрешность γпр положена в основу класса точности электромеханических приборов. В соответствии с ГОСТ 8.401—80 электромеханические приборы поделены на девять классов точности: Самый высокий класс точности — 1-й. самый низкий — 9-й. Класс точности выражается в процентах, всегда указывается на лицевой панели прибора цифрами (без знака %) и является сравнительной характеристикой приборов. Если в формулу (2.2) подставить абсолютную погрешность, выраженную формулой (2.3), то получим формулу, связывающую γпр и γд γд = γпр Хn/Ад (1.5) Большинство электронных приборов на классы точности не делятся. Значения абсолютной или относительной погрешностей приводятся в техническом паспорте в виде конкретного числа или формулы. Например, в паспорте низкочастотного генератора ГЗ-107 приведена действительная относительная погрешность установки частоты F: γдF=±[3+30/F]% Погрешность косвенных измерений определяют по формуле γд= (k1*γд1) + (k2 *γд2)+….( kn *γn) (1.6) где k1; k2;…kn; - показатели степени (могут быть положительными или отрицательными, целыми или дробными числами); γд1; γд2;…… γn; -действительные относительные погрешности прямых измерений. Действительная и приведенная относительные погрешности могут быть как положительными, так и отрицательными. На практике чаще всего формула (1.6) ограничивается двумя слагаемыми. В основу косвенных измерений положены известные зависимости, приведенные в табл. 2.1. Таблица 2.1. Формулы расчета параметров, используемые при косвенных измерениях
Точность ν и действительная относительная погрешность измерения связаны обратной зависимостью: ν=1/ γд (1.7) Примеры решения типовых задач Задача № 1. Измерено два значения напряжения (50 и 400 В) вольтметром с номинальным значением 400 В с одной и той же абсолютной погрешность 0,5 В. Какое напряжение будет измерено с меньшей погрешностью? Решение. При решении задач по определению погрешности измерений необходимо правильно обозначить в символах исходные данные. Так, напряжение измеряется рабочим вольтметром, которое является действительным измеренным значением (Ад) и обозначается U1 = 50 В, U2 — 400 В, с одинаковой абсолютной погрешностью ∆1= ∆2 = 0,5 В. О виде шкалы вольтметра ничего не говорится, значит используется вольтметр с односторонней шкалой, у которого Амин = 0 и Амах = 400 В, поэтому Хn = 400В. Погрешность измерения определяем по формуле (1.2): γд = ±(∆/ Ад)*100% γд1 = ±(∆/ U1)*100% =(0,5В/50В)*100%=1% γд2 = ±(∆/ U2)*100% =(0,5В/400В)*100%=0,125% Один и тот же вольтметр измерит напряжения 50 и 400 В с погрешностями, одна из которых в 8 раз больше другой.. Причину такого различия объясняет анализ графика (см. рис.1) при измерении U1 в 50 В стрелка индикатора вольтметра будет находиться в 1-й четверти шкалы (рис. 2.2, а), а при измерении U 2 —в 400 В — в 4-й четверти (рис. 2.2, б). Ответ: с меньшей погрешностью будет измерено напряжение 400 В. 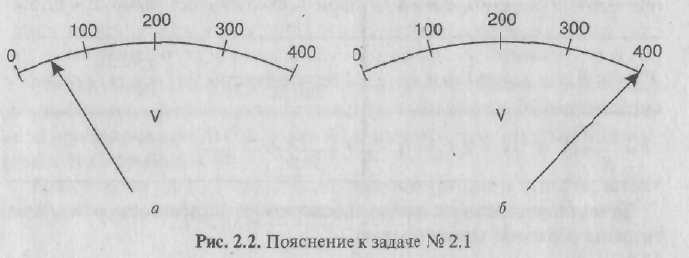 ЗАДАНИЕ 1.Решить ряд задач и определить данные Решить задачу №1. Врезультате калибровки вольтметра магнитоэлектрической системы со шкалой 0...50 В и шагом шкалы 10 В получены показания образцового вольтметра (табл. 2.2). Определить относительную приведенную погрешность и назначить вольтметру класс точности. Таблица 2.2. Исходные данные для задачи №1
Для определения γпр необходимо воспользоваться формулой (1.3): γпр=± (∆мах/ Хn) *100% Решите и запишите вывод.  Решить задачу №2. Необходимо измерить напряжение 20 В многопредельным вольтметром 5-го класса точности (0,5%) с пределами измерения 7,5 — 15 — 30 — 60 В. Выбрать оптимальный предел измерения вольтметра и оценить погрешность в выбранном пределе измерения. При выборе предела измерения целесообразно представить положение стрелки вольтметра при измерении заданного параметра в каждом из четырех пределов (рис. 2.3). Решите и запишите выводы. Решить задачу № 3. Определить абсолютную и действительную относительную погрешности установки частоты 90 Гц на генераторе ГЗ-107, если в паспорте прибора указано, что действительная относительная погрешность установки частоты определяется по формуле γдF=±[3+30/F]% По формуле (1.2) γд = ±(∆/ Ад)*100% определим абсолютную погрешность установки заданной частоты. Решите и запишите выводы. Решить задачу № 4. Для измерения сопротивления или мощности косвенным методом использовались два прибора: амперметр и вольтметр магнитоэлектрической системы. Определить: 1. Величину сопротивления и мощность по показаниям прибора. 2. Максимальные абсолютные погрешности амперметра и вольтметра. 3. Абсолютную погрешность косвенного метода. 4. Относительную погрешность измерения. 5. Пределы действительных значений измеряемых физических величин. Результаты вычислений сопротивлений и мощности свести в таблицу 3. Таблица 3– Результат вычислений.
Таблица 1 – Исходные данные для задачи
ЗАДАНИЕ 2.Дайте ответы на контрольные вопросы. КОНТРОЛЬНЫЕ ВОПРОСЫ 1.Что называется погрешностью? 2.Назовите основные характеристики погрешности измерения. 3.Как определить действительную относительную погрешности измерения? 4.Как связаны точность и действительная относительная погрешность измерения? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
