Теория автоматического управления_Оценка исследования систем автоматического управления при случайных воздействиях. Вид работы Курсовая работа Название дисциплины Теория автоматического управления Тема Оценка исследования систем автоматического управления при случайных воздействиях Фамилия студента
 Скачать 432.5 Kb.
|
Основные данные о работе
СодержаниеВведение…………………………………………………………………………………3 Основная часть………………………………………………………………………….4 1 Теория случайных сигналов…………………………………………………...…...4 2 ФАПЧ………………………………………………………………………………..10 3 Моделирование ФАПЧ……………………………………………………………..15 Заключение…………………………………………………………………………….19 Глоссарий………………………………………………………………………………21 Список использованных источников………………………………………………...23 Приложения……………………………………………………………………………25 ВведениеТеория управления является разделом современной науки и техники. Она базируется как на фундаментальных дисциплинах (математика, физика, химия), так и на прикладных дисциплинах (электроника, микропроцессорная техника, программирование). Непрерывное развитие в области промышленности требует постоянного внедрения новых технологий в процесс производства (транспорт, машиностроение, электротехника). Так же с каждым годом все больше возрастают объемы выпускаемой продукции и для оптимизации рабочего процесса все больше внимания уделяется внедрению современных систем управления с участием человека-оператора (автоматизированные) и без него (автоматические). Примером систем автоматического управления являются: различные следящие радиолокационные системы, автоматическая система управления сфетофора и др. В данной работы в качестве системы автоматического управления рассматривается система фазовой автоподстройки частоты. Фазовая автоподстройка частоты является многофункциональной системой, использующейся для частотной синхронизации, уплотнения и разделения каналов в системах связи, умножения и преобразования частоты, а также в других целях. Целью данной курсовой работы является исследование системы фазовой автоподстройки частоты при случайных воздействиях. Для выполнения цели были поставлены следующие задачи: рассмотреть теорию возникновения случайных сигналов и их основные характеристики; проанализировать принцип работы системы автоматического управления на примере ФАПЧ; провести моделирование исследуемой системы на базе Matlab. Основная часть1 Теория случайных сигналовСлучайной величиной называется величина, которая в результате опыта принимает то или иное значение, какое именно ─ зависит от привходящих обстоятельств и заранее предсказано быть не может. Для задания случайной величины нужно указать, во-первых, ее возможные значения и, во-вторых, установить в той или иной форме зависимости между вероятностями этих возможных значений [1]. Для задания вероятностей возможных значений в теории вероятностей применяют функции распределения вероятностей, плотности вероятности и характеристические функции. Приведем их определения. Функция распределения вероятности F(x) случайной величины ξ есть вероятность того, что случайная величина ξ, принимает значение, меньшее, чем произвольное вещественное число х:  .Зная функцию распределения, можно найти вероятность того, что случайная величина будет заключена в полуинтервале xl ≤ ξ ≤ х2:  .Производная от функции распределения p(x)=dF/dx есть плотность распределения вероятности данной случайной величины. Очевидно, что  ,то есть величина p(x)=dx есть вероятность попадания случайной величины ξ в полуинтервал (x, x+dx]. В статистической теории сигналов широко применяются особые числовые характеристики случайных величин, называемые их моментами. Простейшим является момент первого порядка, так называемое математическое ожидание:  ,которое служит теоретической оценкой среднего значения случайной величины, получаемого в достаточно обширных сериях испытаний. Используются также центральные моменты случайных величин, важнейший центральный момент – так называемая дисперсия:  .Величина σx, т. е. квадратный корень из дисперсии, называется средним квадратическим отклонением, которое служит для количественного описания меры разброса результатов отдельных случайных испытаний относительно математического ожидания. Количественной характеристикой степени статистической связи двух случайных величин служит их корреляционный момент R12 , определяемый как среднее значение произведения  : .Теория случайных величин изучает вероятностные явления «в статике», рассматривая их как некоторые зафиксированные результаты экспериментов. Для описания сигналов, которые отображают развивающиеся во времени случайные явления, методы классической теории вероятностей оказываются недостаточными. Подобные задачи изучает особая ветвь математики, получившая название теории случайных процессов. По определению, случайный процесс X(t) — этo особого вида функция, характеризующаяся тем, что в любой момент времени t принимаемые ею значения являются случайными величинами. Пусть X(t) — случайный процесс, заданный ансамблем реализаций, a t1 ─ некоторый произвольный момент времени. Фиксируя величины (x1(t1), x2(t1), x3(t1), …. xk(t1)) получаемые в отдельных реализациях, осуществляем одномерное сечение данного случайного процесса и наблюдаем случайную величину X(tt). Ее плотность вероятности р(х, tt) называют одномерной плотностью вероятности процесса X(t) в момент времени tt. Согласно определению, величина dP = p(x, t1)dx есть вероятность того, что реализации случайного процесса в момент времени t1, примут значения, лежащие в интервале (х, х + dx). Информация, которую можно извлечь из одномерной плотности, недостаточна для того, чтобы судить о характере развития реализаций случайного процесса во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в несовпадающие моменты времени t1 и t2. Возникающая при таком мысленном эксперименте двумерная случайная величина {X(t1), X(t2)} описывается двумерной плотностью вероятности р(х1, х2, t1, t2). Эта характеристика случайного процесса позволяет вычислить вероятность события, заключающегося в том, что реализации случайного процесса при t = t1 проходит в малой окрестности точки х1, а при t = t2 — в малой окрестности точки x2. Менее детальные, но, как правило, вполне удовлетворительные в практическом смысле характеристики случайных процессов можно получить, вычисляя моменты тех случайных величин, которые наблюдаются в сечениях этих процессов. Поскольку в общем случае эти моменты зависят от временных аргументов, они получили название моментных функций. Для теории сигналов наибольшее значение имеют три моментные функции низших порядков, называемые математическим ожиданием, дисперсией и функцией корреляции. Математическое ожидание:  .Дисперсия:  .Функция корреляции:  .Случайные процессы, статистические характеристики которых одинаковы во всех сечениях, называются стационарными случайными процессами. Стационарный случайный процесс называют эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени. Операция усреднения выполняется над единственной реализацией х(t), длительность Т которой теоретически может быть сколь угодно велика. Математическое ожидание эргодического случайного процесса:  .Дисперсия подобного процесса:  .Функция корреляции:  .Из-за вероятностного характера отдельных реализаций прямой перенос методов спектрального анализа в теорию случайных процессов невозможен. Однако удаётся получить ряд важных спектральных характеристик случайных колебаний, применяя методы Фурье-анализа для некоторых функций, получаемых путём усреднения реализаций. Спектр мощности W() и функция корреляции R() случайного процесса связаны между собой преобразованием Фурье:   Данные формулы составляют содержание теоремы Винера Хинчина. В технических расчётах часто вводят односторонний спектр мощности N(f), представляющий собой среднюю мощность случайного процесса, приходящуюся на интервал частот в 1 Герц: 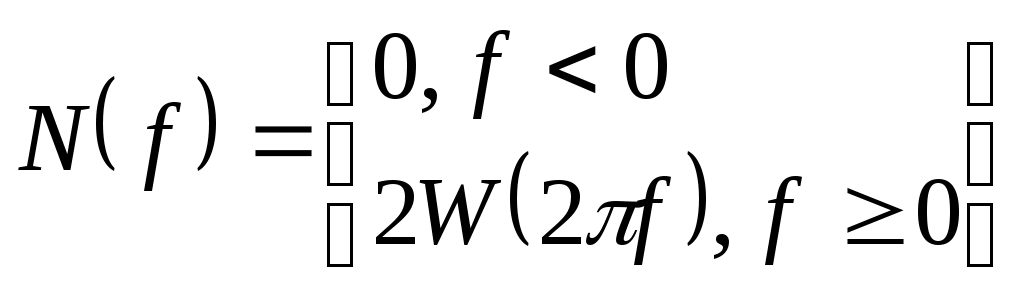 .При этом легко видеть, что  .В теории сигналов белым шумом принято называть стационарный случайный процесс, спектральная плотность мощности которого равномерно распределена на всех частотах: W() = W0 = const. Белый шум является абстрактной математической моделью и отвечающий ему физический процесс в природе, безусловно, не существует. Однако это не мешает приближённо заменять реальные достаточно широкополосные случайные процессы белым шумом в тех случаях, когда полоса пропускания цепи, на которую воздействует случайный сигнал оказывается значительно уже эффективной ширины спектра шума. Выводы по первой главе: рассмотрели кратко математическое описание возникновения случайных сигналов и их основные характеристики (математическое ожидание, дисперсия, функция корреляции). 2 ФАПЧДля оценки исследования случайных воздействий на системы автоматического управления рассмотим в качестве примера устройство для фазовой автоподстройки частоты. Системой фазовой автоподстройки частоты (ФАПЧ) называется система автоматического регулирования, обеспечивающая автоматическое регулирование частоты управляемого генератора в устройствах приема и обработки сигналов в соответствии с частотой входного сигнала и использующая в качестве измерительного элемента фазовый детектор [2]. Системы ФАПЧ используются для подстройки частоты гетеродина в супергетеродинных радиоприемных устройствах, выделения несущей частоты в демодуляторах систем передачи сообщений, при реализации когерентного приема сигналов, измерения частоты с помощью узкополосных следящих фильтров, при формировании высокостабильных колебаний в синтезаторах частот различных радиотехнических устройств и т. д. [3] Системы ФАПЧ могут быть реализованы в аналоговом и цифровом виде. Особенностью системы ФАПЧ (находящейся в состоянии синхронизации) является нулевая статическая ошибка по частоте, т. е. равенство частот колебаний подстраиваемого генератора (гетеродина)  и эталонного (входного) колебания  . Вместе с тем в электронных системах ФАПЧ существует статическая ошибка регулирования по фазе, т, е. статическое отличие фаз колебаний подстраиваемого генератора, управляемого напряжением (ГУН), и эталонного сигнала. Системы ФАПЧ обычно имеют сравнительно узкий диапазон начальных расстроек, в котором они осуществляют подстраивающее действие. При анализе работы системы ФАПЧ рассматривают режимы удержания и захвата.Режимом удержания называется установившийся режим равенства частот  , соответствующий эффективной работе системы ФАПЧ при медленных изменениях начальной расстройки. При этом имеются в виду изменения, скорость которых много меньше скорости переходных процессов в системе.Режимом захвата называется процесс, возникающий при скачкообразном изменении начальной расстройки и заканчивающийся установлением режима удержания. Характерным различием этих режимов является то, что в режиме захвата существенную роль играют переходные процессы. Основными характеристиками систем ФАПЧ являются следующие: • Полоса удержания  - область начальных расстроек ГУН, внутри которой система ФАПЧ эффективно работает в режиме удержания.• Полоса захвата  - область начальных расстроек ГУН, внутри которой система ФАПЧ эффективно работает в режиме захвата.• Время захвата t3 - время втягивания системы ФАПЧ в режим синхронизации, существенно зависящее от значения начальной расстройки между частотой входного колебания и частотой колебания ГУН. Основными элементами структурной схемы системы фазовой автоподстройки частоты (рисунок 1) являются: фазовый детектор - ФД, фильтр низкой частоты - ФНЧ, усилитель - УС, управляющий элемент УЭ и перестраиваемый (синхронизируемый) генератор - ГУН.  Рисунок 1 – Структурная схема системы ФАПЧ На один вход фазового детектора ФД поступает сигнал , на второй - высокочастотное колебание синхронизируемого перестраиваемого генератора. Между выходом ФД и входом управляющего элемента в петле обратной связи находятся фильтр низкой частоты ФНЧ и усилитель постоянного тока УС. Именно эти два элемента структурной схемы практически формируют частотную характеристику системы ФАПЧ и определяют ее петлевой коэффициент передачи. Если частота сигнала ωс и частота колебания на выходе ГУН ωг отличаются друг от друга на постоянную величину Δω, то мгновенное значение разности фаз φ между ними будет равно:
Если разность частот двух колебаний не постоянна во времени, то мгновенное значение разности фаз можно определить по формуле:
откуда
Обычно в качестве фазового детектора ФД (рисунок 1) используется аналоговый перемножитель, имеющий на выходе фильтр нижних частот, пропускающий лишь колебание разностной частоты. Тогда на выходе этого перемножителя будет присутствовать колебание вида:  ,где  коэффициент передачи фазового детектора (аналогового перемножителя).Если положить коэффициент передачи ФНЧ в полосе пропускания KФНЧ=1, то напряжение на входе управляющего элемента УЭ будет пропорционально косинусу текущего сдвига фаз между колебаниями:  ,где  , k - коэффициент передачи петли обратной связи.Управляющее напряжение используется в системе ФАПЧ для подстройки генератора, управляемого напряжением ГУН. Изменение частоты ωг будет определяться изменением сдвига фаз φ(t). Рассмотрим подробнее режимы работы системы ФАПЧ [4]. В зависимости от начальной разности частот ωн входного колебания ωС и частоты ГУН ωГ0 при разомкнутой петле обратной связи система ФАПЧ может находиться в различных режимах (рисунок 2). На этом рисунке прямая линия Δω = ωн соответствует разомкнутой петле обратной связи системы ФАПЧ.  Рисунок 2 – Зависимость разности частот входного сигнала ωс и сигнала ГУН ωг от величины ωн Когда начальная расстройка ωН больше полосы удержания ΔΩУ, в системе ФАПЧ наблюдается режим биений, для которого характерно отсутствие равенства частот ГУН и входного сигнала, т. е. ωС≠ ωГ. В этом режиме разность фаз входного колебания и колебания ГУН непрерывно возрастает, а напряжение UФД (t) на выходе фазового детектора изменяется, представляя собой колебательное напряжение переменной частоты. Средняя частота биений меньше начальной расстройки ωН. Если начальная расстройка увеличивается, то средняя частота биений асимптотически стремится к ωН (рисунок 2). Наличие ФНЧ на выходе фазового детектора ФД при прочих равных условиях приводит к уменьшению амплитуды биений по сравнению со случаем рассмотрения системы ФАПЧ без ФНЧ, т. е. к затруднению ввода системы в состояние синхронизации. Именно поэтому в системах ФАПЧ с ФНЧ полоса захвата всегда меньше полосы удержания (см. рисунок 2). При достижении величиной |ωН| значения ΔΩЗ/2 средняя частота биений стремится к нулю, т. е. через время tЗ частота ГУН и частота входного сигнала становятся одинаковыми, и система ФАПЧ переходит в режим захвата. На практике полосу захвата ΔΩЗ (рисунок 2) определяют по моменту синхронизации частот ГУН и входного сигнала при изменении |ωН| от больших значений к малым. При наличии синхронизации и изменении расстройки |ωН| от нулевого значения в сторону увеличения очевидно, что биения колебаний будут отсутствовать вплоть до момента срыва синхронизации при |ωН|≈ ΔΩУ/2. Выводы по второй главе: выбрали объект исследования (ФАПЧ) для более детального рассмотрения воздействия случайных на систему. Рассмотрели и описали основные узлы системы и характеристики. 3 Моделирование ФАПЧДля проверки теоретических данных проведем моделирование системы ФАПЧ в среде Matlab [5]. В состав модели входят: генератор гармонических колебаний с постоянной частотой (Sine Wave), генератор с линейно-изменяющейся частотой (Chirp Signal), генератор белого шума, фазовый детектор, состоящий из перемножителя и ФНЧ, полосовой фильтр, три вида фильтров обратной связи, усилитель и генератор, управляемый напряжением(ГУН). Общее время моделирования равно 10 с. Структурная схема модели представлена на рисунке 3.  Рисунок 3 − Структурная схема системы ФАПЧ в пакете динамических систем «Simulink В результате анализа подобраны параметры имитационной модели. Частота ЭГ равна 1000 Гц, амплитуда 1В, сигнал синусоидальной формы. Начальная частота генератора с линейно изменяющейся частотой (Initial frequence), равна 900 Гц, конечная частота (Frequence at target time) равна 1100 Гц, время изменения частоты (Frequence at target time) - 10 сек. При таких настройках генератор линейно- изменяющейся частоты изменяет свою частоту на 20 Гц каждую секунду, на пятой секунде данный генератор имеет номинальную частоту, равную 1000 Гц. Частота покоя ГУН равна 1000 Гц, крутизна (Input sensitivity) - 5 Гц/В, начальная фаза равна нулю. Коэффициент передачи в петле обратной связи равен 10. Полосовой фильтр имеет четвертый порядок, нижняя частота 900 Гц, верхняя 1100 Гц. ФНЧ, входящий в состав фазового детектора, также имеет четвертый порядок и полосу пропускания 200 Гц. В процессе исследования нами рассматривались следующие варианты построения системы: ФАПЧ без фильтра; ФАПЧ с интегрирующим фильтром нижних, постоянная времени Т1 = 0,1 секунды; ФАПЧ с пропорционально интегрирующим фильтром, постоянная времени Т2 = 0,1 секунды, Т3 = 0,03 секунды; ФАПЧ с изодромным фильтром, постоянная времени Т4 = 0,2 секунды. С помощью имитационной модели системы ФАПЧ проведем измерение полос захвата и удержания при различных вариантах системы: Система без фильтра (рисунок 4):  Рисунок 4 − Сигнал на выходе фазового детектора Измерения проводились при входном сигнале с генератора с линейно-меняющейся частотой: полоса захвата: 25 Гц, полоса удержания: 25Гц. Система с интегрирующим фильтром, постоянная времени Т1 = 0,1 секунды (рисунок 5):  Рисунок 5 − Сигнал на выходе фазового детектора Полоса захвата:10 Гц (измерена при помощи генератора постоянной частоты). Полоса удержания: 25 Гц. ФАПЧ с пропорционально-интегрирующим фильтром, постоянная времени Т2= 0,1с, Т3 = 0,03 с (рисунок 6):  Рисунок 6 − Сигнал на выходе фазового детектораПолоса захвата: 6 Гц; полоса удержания: 25 Гц. ФАПЧ с фильтром астатизма второго порядка, постоянная времени Т4= 0,2 секунды. Для измерения полос захвата и удержания был использован ЭГ. Постепенно изменяя начальную расстройку между ЭГ и ГУН, получены следующие значения частот: полоса захвата: 25 Гц, полоса удержания: 25 Гц. Система ФАПЧ при воздействии шумов подвержена срыву слежения. Существует несколько методов анализа срыва слежения. В настоящем исследовании рассмотрен метод теории выбросов. В данном методе под срывом слежения подразумевается выход фазы сигнала ГУН за пределы апертуры фазового детектора [6]. Расчеты приведены в приложении А. На рисунке 7 изображена полученная зависимость вероятности срыва слежения от отношения мощностей эталонного сигнала и шума.  Рисунок 7 − Зависимость вероятности срыва слежения от отношения сигнал/шум q2 Краткий вывод по третьей главе: в данной работе исследованы принципы работы фазовой автоподстройки в разработанном программном обеспечении в среде Matlab.Определены полосы захвата и удержания при различных вариантах системы. Методом теории выбросов проведен анализ срыва слежения в системе с интегрирующим фильтром. По результатам расчета построена зависимость вероятности срыва слежения от отношения сигнал/шум. ЗаключениеСистемы ФАПЧ находят широкое применение в микроэлектронных компонентах, производимых известными фирмами. Так, например, фирма Analog Devices использует систему ФАПЧ: в одно- и двухканальных синтезаторах ADF410x/1x/5x и ADF420x/1x/5x типов “Integer-N” и “Fractional-N” с программируемыми (перестраиваемыми) частотами до 3,7 ГГц; для умножения тактовой частоты в ЦАП серии TxDAC+ AD9751/3/5 (300 МГц), AD9772/4 (400/128 МГц), в цифровых (DDS) синтезаторах-модуляторах AD9852/4 (300 МГц) и модуляторах AD9853/6 (168/200 МГц); для умножения частоты в k = 2N/n раз, где n − целое число из ряда 1, 2, ... 2N/2,5, − с DDS-синтезаторами AD9850/1/2/4 в качестве делителей частоты в цепи обратной связи (например, при N = 48 и максимальной частоте после умножения 300 МГц при использовании AD9852); в качестве частотного модулятора, совмещённого с синтезатором частот, и частотного демодулятора, совмещённого с пребразователем частоты, − в микросхеме приёмопередатчика AD6411 системы DECT; в качестве квадратурного модулятора, совмещённого с квадратурным преобразователем частоты, − в микросхеме приёмопередатчика AD6523, применяемого совместно с синтезатором AD6524 (также на базе ФАПЧ), − в системах GSM и DCS; в качестве источника опорной частоты с квадратурным выходом для демодулятора в микросхеме приёмопередатчика AD6432 системы GSM. Фирма Texas Instruments использует систему: в двух- и трехканальных синтезаторах частот TRF2020 − до 0,25, 0,25 и 1,2 ГГц, TRF2050 − до 0,25 и 1,2 ГГц, TRF2052 − до 0,15 и 2,0 МГц и TRF3040, являющимся также модулятором, − до 0,2 и 2,0 ГГц; для синтеза сигналов опорной частоты для модуляторов в микросхемах TRF3040 и TRF3520; для умножения тактовой частоты в цифровых сигнальных процессорах TMS320C54x, TMS320C62x, TMS320C67x и TMS320VC33. Фирма Motorola (Semiconductor Product Sector) использует систему в двухканальных синтезаторах частот MC145181 (до 550 и 60 МГц), MC145225 (до 1,2 и 0,55 ГГц), MC145230 (до 2,2 и 0,55 ГГц) и др., предназначенных для аппаратуры радиосвязи различных систем. Фирма Gran-Jansen AS (Норвегия) использует систему ФАПЧ в приёмопередатчике GJRF400 (GJRF10), работающем в диапазоне частот 300–500 МГц, для синтеза опорного колебания и для аналоговой частотной модуляции. Курсовая работа – самостоятельная разработка конкретной темы по изучаемой дисциплине с элементами научного анализа, предназначенная для формирования у обучающихся теоретических знаний и практических навыков, умений работать с литературой, анализировать источники, делать обстоятельные и обоснованные выводы. В процессе выполнения курсовой работы: провели систематизацию и закрепление знаний, полученных в рамках курса «Теория автоматического управления»; исследовали принцип работы фазовой автоподстройки с различными фильтрами низких частот в петле обратной связи и получение характеристик срыва слежения; освоили систему моделирования Matlab. Глоссарий
Список использованных источников
Приложения
|
