Практика ТПР. Выделяются три основных требования

Название	Выделяются три основных требования
Анкор	Практика ТПР
Дата	10.06.2021
Размер	72.32 Kb.
Формат файла
Имя файла	Zadanie_1_Vyskrebentsev_I_S.docx
Тип	Документы #216278

Характерная особенность процесса принятия решений при управлении производственными объектами, в которых особая роль принадлежит человеку, состоит не только в необходимости использования компьютерных систем, но и в привлечении суждений руководителей, специалистов – ЛПР. Информация, получаемая на основе суждений ЛПР, позволяет выявить его предпочтения относительно значений критерия, при составлении значений различных критериев и очень важна для выбора решения.
Выделяются три основных требования:

1. валидность;

2. надежность;

3. различительная способность.

3. Для критерия А-оптимальности матрицах выбирается так, чтобы достигнуть минимума суммы квадратов длин главных осей эллипсоида рассеяния. Алгебраически это соответствует минимуму еще одной функции матрицы дисперсий-ковариаций, которая называется следом и обозначается trM"¹ или spM^-1. Следом квадратной матрицы называется сумма ее диагональных элементов. Вспомним, что на диагонали матрицы М^¹ находятся дисперсии Ь-коэффициентов, значит, А-опти- мальность обеспечивает минимум суммы дисперсий Ь-коэф- фициентов без учета их ковариаций и, следовательно, минимум средней дисперсии.

4. Собственно, дерево решений — это метод представления решающих правил в иерархической структуре, состоящей из элементов двух типов — узлов (node) и листьев (leaf). В узлах находятся решающие правила и производится проверка соответствия примеров этому правилу по какому-либо атрибуту обучающего множества.

В простейшем случае, в результате проверки, множество примеров, попавших в узел, разбивается на два подмножества, в одно из которых попадают примеры, удовлетворяющие правилу, а в другое — не удовлетворяющие.

5. В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям^[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения ^[1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.

6. Парето-оптимальные решения (еще называют – эффективные решения, недоминируемые решения), проведя аналогию с обычными оптимальными решениями при одном показателе. Пусть имеется только один показатель, по которому сравниваются альтернативы – F. Ясно, что оптимальной по этому показателю будет та альтернатива x*, для которой выполняется условие: F(x*) >= F(x) – оценка альтернативы по показателю лучше (или не хуже), чем оценки F у всех остальных альтернатив. Аналогично и для векторного критерия – альтернатива xp принадлежит множеству Парето-оптимальных, если выполняется условие:

(f1, f2, …,fN) (xp) >= (f1, f2, …,fN) (x),

где x не принадлежит ХP ;

”>=” – означает “больше или равно”.

Эта запись означает, что для всех fi верно fi(xp) >= fi(x) и есть хотя бы один показатель fjтакой, что fj(xp) > fj(x). В этом случае можно говорить, что xp лучше (предпочтительнее), чем x, для чего будем использовать следующую запись: xp } x.

7. Структурированная задача — задача, где известны все ее элементы и взаимосвязи между ними.

В структурированной задаче удается выразить ее содержание в форме математической модели, имеющей точный алгоритм решения. Подобные задачи обычно приходится решать многократно, и они носят рутинный характер.

Слабоструктурированные задачи – это задачи, в которых существуют количественные и качественные характеристики, при этом число качественных параметров значительно превосходит количественные.
Неструктурированная (неформализуемая) задача - задача, в которой невозможно выделить элементы и установить между ними связи. Решение неструктурированных задач из-за невозможности создания математического описания и разработки алгоритма связано с большими трудностями.

Управленческие решения можно классифицировать по ряду признаков.

1. По степени уникальности. Запрограммированные решения, результат заранее определенной последовательности шагов или действий. Руководитель часто программирует решения под ситуации, повторяющиеся с определенной периодичностью. Незапрограммированные решения, возникающие в ситуациях, которые в определенной степени новы, неструктурированы и сопряжены с неизвестными факторами.

2. По степени воздействия на будущее. Оперативные — решения по обеспечению максимизации прибыльности от текущих производственно-хозяйственных операций. Основная сфера решений — распределение имеющихся ресурсов предприятия между функциональными подразделениями, оперативное планирование, регулирование и контроль производственно-хозяйственных процессов на предприятии. Тактические (административные) — решения о структуризации ресурсов предприятия, обеспечивающие максимальную результативность. Принятие решений в области структуры организации (структурное построение организации и делегирование полномочий), организация производственных и информационных потоков, каналы товародвижения и т. п. Стратегические — решения о целях и задачах предприятия, сферах деятельности, целевых рынках, обеспечивающих стабильный рост и потенциальную результативность предприятия.

3. По числу лиц принимающих решения. Индивидуальные, принимаемые единолично. Коллективные, принимаемые на основе заранее оговоренных условий (простое большинство, квалифицированное большинство, консенсус и т. п.)

4. По степени определенности ситуации. Решения, принимаемые в условиях определенности (детерминистские решения). Лицо принимающее решение знает последствия развития ситуации по каждой из возможных альтернатив. Решения, принимаемые в условиях риска (вероятностные решения). Последствия развития ситуации не известны, но известными являются вероятностные характеристики возможных в будущем событий. Решения, принимаемые в условиях неопределенности, то есть в условиях, когда отсутствуют вероятностные оценки потенциальных результатов (исходов событий). В этой ситуации требуется: получение дополнительной информации для снижения степени неопределенности, предположение о вероятности возможных событий на основе опыта и интуиции.

5. По сроку действий последствий решений: долгосрочные, среднесрочные, краткосрочные.

6. По способам принятия решений. Интуитивные решения. Выбор основан на ощущении, что выбор правилен (озарение или шестое чувство). Интуитивные решения могут приниматься с учетом знаний и накопленного опыта. Например, принятие рутинных решений при неизменности внутренней и внешней ситуации. Рациональные решения. Выбор основан на результатах аналитического процесса, имеющего определенную последовательность взаимосвязанных шагов.

7. По масштабам. Глобальные — такие решения являются обязательными для исполнения всей организации. Локальные затрагивают конкретные структурные подразделения предприятия, определенные сферы его деятельности.

8. Рассмотрим пример области Парето в континуальном множестве. Для этого изобразим на плоскости двухкритериальное пространство достижимости, которое ограничено частично выпуклой замкнутой кривой.

9. Переговорный процесс — специфический вид совместной деятельности. Ее особенность заключается в том, что цели и интересы, а тем более позиции сторон не совпадают. Каждая из сторон складывает стратегию так, чтобы им было выгодно. Причем, о стратегии «ВЫИГРАТЬ-ВЫИГРАТЬ» не идет и речи.

10. Здесь и в дальнейшем игрой будет называться совокупность правил, определяющих возможные действия участников игры - игроков. Ранее мы уже упоминали термин "стратегия", понимая под ним синоним к словам "план", "поведение", "управление". В теории игр стратегия - это система поведения, в простейшем случае выбор одной из имеющихся у игрока альтернатив. Игра заканчивается платежом проигравшего игрока выигравшему. Следовательно, должна быть задана функция выигрыша - правило, сопоставляющее величину выигрыша избранной паре стратегий.

В случае игры двух лиц естественно считать их интересы прямо противоположными - игра антагонистическая. Таким образом, выигрыш одного игрока равен проигрышу другого (сумма выигрышей обоих игроков равна нулю, отсюда и название - игра с нулевой суммой). Будем рассматривать игры, в которых у каждого игрока имеется конечное число альтернатив. Функция выигрыша для такой игры двух лиц с нулевой суммой может быть задана в матричной форме (в виде платежной матрицы).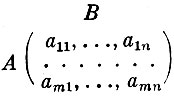

Отсюда название подобных игр - матричные игры. Поясним, как происходит одноходовая игра. Игрок А выбирает одну из m строк (i-ю) платежной матрицы. Не зная результата его выбора, игрок В выбирает один из n столбцов (j-й) той же матрицы. Элемент a_ij определяет сумму выигрыша одного игрока и проигрыша (-a_ij) другого игрока.

Основной вопрос, который возникает здесь, состоит в следующем: существуют ли наилучшие, оптимальные способы ведения игры для каждого из игроков, т. е. имеются ли у них оптимальные стратегии? Поясним, в каком смысле следует понимать оптимальность стратегий. Каждый игрок считает своего противника "разумным", т. е. старающимся выиграть у него как можно больше. При таком предположении естественно считать стратегии игроков оптимальными, если один из них, например первый, не уменьшит своего выигрыша при любом изменении стратегии второго игрока. Соответственно второй игрок не увеличит своего проигрыша при любом изменении стратегии первого игрока. Прежде чем дать ответ на поставленный вопрос, рассмотрим несколько примеров.

11. Для мультипликативного метода подход к решению аналогичен, только целевая функция имеет вид

, причем

.

Основной и очень существенный недостаток методов свертывания критериев состоит в субъективности выбора коэффициентов

.

12. Седловая точка – это пара оптимальных стратегий (A_i, B_j). В этом случае число a=b называется (чистой) ценой игры (нижняя и верхняя цена игры совпадают). Это означает, что матрица содержит такой элемент, который является минимальным в своей строке и одновременно максимальным в своем столбце.

Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. Является точкой равновесия в чистых стратегиях.

Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.

Доказательство.

При любых x ∈ X, y ∈ Y мы имеем f (x, y) ≤ sup x f (x, y). Перейдем к инфимуму по y ∈ Y в обеих частях неравенства. inf y f (x, y) ≤ inf y sup x f (x, y). Справа в этом неравенстве стоит некоторая константа. Перейдя к супремуму по x, получим sup x inf y f (x, y) ≤ inf y sup x f (x, y). Определение антагонистической игры. Ситуация равновесия в антагонистической игре. Существование седловых точек. Смешанные расширения бескоалиционных игр Ситуация равновесия в смешанных стратегиях в бескоалиционных играх Теорема Нэша Следствие. Если в исходном неравенстве достигаются внешние экстремумы, то max x inf y f (x, y) ≤ min y sup x f (x, y). Если, кроме того, достигаются внутренние экстремумы, т.е. при любом x ∈ X существует min y f (x, y) и при любом y ∈ Y существует max x f (x, y), то max x min y f (x, y) ≤ min y max x f (x, y).

Теорема (о необходимых и достаточных условиях существования седловой точки ядра). Пусть существуют и являются конечными минимаксное и максиминное значения ядра M(x,y), , , антагонистической игры. Тогда необходимым и достаточным условием существования седловой точки этого ядра является справедливость равенства указанных выше минимаксного и максиминного значений, т.е.

( 6.7)

В случае выполнения равенства (6.7), значения его левой и правой частей совпадают со значением ядра в седловой точке, т.е. совпадают с величиной M(x^*,y^*).

Сетевое Планирование и Управление включает следующие этапы: - определяется перечень событие и работ; - строится сетевой график; - рассчитываются параметры сетевого графика и определяется длительность критического пути; - производится анализ сетевого графика и его оптимизация. Основными понятиями сетевых моделей являются понятия события и работы.
Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.
Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если a_ij ≥ a_kj для всех j Э N и хотя бы для одного j a_ij > a_kj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.

Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.

Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.

Если первый игрок использует чистые стратегии с вероятностями

, то вектор

называется смешанной стратегией первого игрока. Иначе говоря, это "смесь" чистых стратегий. При этом сумма этих вероятностей равна единице:

Из определений строгого доминирования следует, что доминирующая стратегия дает игроку выигрыш не меньший, чем доминируемая. Поэтому в матрице Н доминируемые стратегии (строки или столбцы) могут быть отброшены, что и приводит к матрице меньших размеров. Однако следует отметить, что исключение доминируемых стратегий может привести к потере некоторых решений; если же исключаются только строго доминируемые стратегии, то множество решений игры не изменяется. В результате применения доминирования получается игра, эквивалентная исходной в смысле следующего утверждения.
Пусть первый игрок использует оптимальную стратегию p* , а второй − смешанную стратегию q, в которой qj > 0, j ∈ J′, где J′ − подмножество активных стратегий второго игрока. Необходимо показать, что цена игры ν = E(p* , q).
Общий подход к решению игровых задач состоит в следующем. Найти цену игры ν* и оптимальные стратегии игроков ξ*, η* по имеющейся платежной матрице, действуя по следующей схеме:  установить, имеется или нет в игре седловая точка, которая указывает на цену игры и определяет оптимальные чистые стратегии игроков;  если седловая точка отсутствует, то выяснить, нельзя ли упростить игру;  собственно поиск решения игры каким-либо методом.
Цена игры (или значение игры) [value of game] — общее значение выигрыша одного игрока и проигрыша другого в седловой точке игры, иными словами — значение выигрыша, соответствующего решению игр.

Оптимальная стратегия игрока – стратегия, обеспечивающая наилучшее положение в данной игре, т. е. максимальный выигрыш. Если игра повторяется неоднократно и содержит, кроме личных, случайные ходы, то оптимальная стратегия обеспечивает максимальный средний выигры.

Оценка компонентов вектора приоритетов производится по схеме, представленной в таблице 3.

Таблица 3. Оценка компонентов вектора приоритетов

	A₁	…	A_n
A₁	1	…	W₁/W_n	X₁ = [1×(W₁/W₂)×… ×(W₁/W_n)]1/n	Вес (A₁) = X₁/сумма (X_i)
…	…	1	A_n	…	…
A_n	W_n/W₁	…	1	X_n = [(W_n/W₁)×… ×(W_n/W_n–1)×1]1/n	Вес (A_n) = X_n/сумма (X_i)
				Сумма (X_i)

Приоритеты синтезируются начиная со второго уровня вниз. Локальные приоритеты перемножаются на приоритет соответствующего критерия на вышестоящем уровне и суммируются по каждому элементу в соответствии с критериями, на которые воздействует элемент. Весьма полезным побочным продуктом теории является так называемый индекс согласованности (ИС), который дает информацию о степени нарушения согласованности. Вместе с матрицей парных сравнений мы имеем меру оценки степени отклонения от согласованности. Если такие отклонения превышают установленные пределы, то тому, кто проводит суждения, следует перепроверить их в матрице:
22. Метод Брауна-Робинсон — это итеративная процедура построения последовательности пар смешанных стратегий игроков, сходящейся к решению матричной игры. В 1-ой партии оба игрока выбирают произвольную чистую стратегию. ... Полученные при этом вероятностные распределения определяют смешанные стратегии игроков.

Основная идея метода состоит в следующем.

Разыгрывается «мысленный» эксперимент, в котором игроки А и В поочередно применяют друг против друга свои стратегии, стремясь выиграть побольше. При этом каждый игрок при выборе очередной стратегии ориентируется не на оптимальный выигрыш относительно последней стратегии противника, а на оптимальный «накопленный» выигрыш за все предыдущие ходы. Приближенные оптимальные стратегии игроков определяются относительными частотами применения ими чистых стратегий.

Метод простой итерации — один из простейших численных методов решения уравнений. Метод основан на принципе сжимающего отображения, который применительно к численным методам в общем виде также может называться методом простой итерации или методом последовательных приближений.
Групповой выбор управленческого решения – это процедура принятия коллективного решения на основе согласования индивидуальных предпочтений членов группы. Процедура выбора в данном случае – это согласование индивидуальных предпочтений и выработка коллективного мнения.
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях (для игрока II):
12x₂ ≥ 1
2x₁+11x₂ ≥ 1
7x₁+x₂ ≥ 1
F(x) = x₁+x₂ > min
найти максимум функции Z(y) при ограничениях (для игрока I):
2y₂+7y₃ ≤ 1
12y₁+11y₂+y₃ ≤ 1
Z(y) = y₁+y₂+y₃ > max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции Z(Y) = y₁+y₂+y₃ при следующих условиях-ограничений.
2y₂+7y₃≤1
12y₁+11y₂+y₃≤1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
2y₂+7y₃+y₄ = 1
12y₁+11y₂+y₃+y₅ = 1
Решим систему уравнений относительно базисных переменных: y₄, y₅
Полагая, что свободные переменные равны 0, получим первый опорный план:
Y0 = (0,0,0,1,1)
.
Дерево принятия решений (также называют деревом классификации или регрессионным деревом) — средство поддержки принятия решений, использующееся в машинном обучении, анализе данных и статистике. Структура дерева представляет собой «листья» и «ветки». На рёбрах («ветках») дерева решения записаны признаки, от которых зависит целевая функция, в «листьях» записаны значения целевой функции, а в остальных узлах — признаки, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Есть различные способы выбирать очередной признак:

Алгоритм ID3, где выбор признака происходит на основании прироста информации (англ. Gain), либо на основании критерия Джини.
Алгоритм C4.5 (улучшенная версия ID3), где выбор признака происходит на основании нормализованного прироста информации (англ. Gain Ratio).
Алгоритм CART и его модификации — IndCART, DB-CART.
Автоматический детектор взаимодействия Хи-квадрат (CHAID). Выполняет многоуровневое разделение при расчёте классификации деревьев;[6]
MARS: расширяет деревья решений для улучшения обработки цифровых данных.

В чем парадокс? Парадокс в двух утверждениях (1) обмен выгоден двум игрокам (2) можно даже не открывать свой конверт, а меняться сразу.

Пример: предполагается, что если вы вытянули из конверта какие-нибудь 70 рублей, то это значит, что организаторы либо создали пару (35 рублей в одном конверте, 70 рублей - в другом), либо (70 рублей, 140 рублей) . Вероятность обоих пар одинакова - это отчасти следует из того, что суммы могут быть любыми.

Самое забавное здесь состоит в том, что нет никакого парадокса. Все правильно, включая то, что меняться надо сразу не глядя на свой конверт. Но только при одном условии - что суммы в конверте могут быть любыми. Согласно условию, их размер с одной и той же вероятностью (пусть и выражающейся бесконечно малой величиной) могут быть как 10 рублей, так и бесконечно много рублей. Ведь если есть верхний предел, то вся логика парадокса рушится. Предположим, сумма не может быть выше 1 млн. Вы вынимаете из конверта 1 млн - и все, меняться нельзя, так как вероятность того, что в другом конверте 2 млн равна нулю. Также меняться не выгодно, если вы вынете сразу что-то больше, чем 500 тыс., например, 750 тыс. рублей - в другом конверте просто не может быть 1,5 млн рублей, так как предел равен 1 млн.

Но как только в условиях любой задачи возникает и начинает активно действовать бесконечность, то любые выводы кажутся парадоксальными, но они парадоксальны лишь с точки зрения нашей логики, оперирующей в конечном мире.