кп. 1 часть. Виды нагружения. Напряжение, основные понятия. Реальный объект
 Скачать 2.61 Mb.
|
|
Y″= 1/ρ = Mu/EJz Y - перемещение сечения балки. 1/ρ – кривизна . E – модуль упругости 1 –го рода . Jz – экваториальный момент инерции сечения балки относительно оси z. Величина EJz называется жесткостью бруса при изгибе. Исключая кривизну из предыдущей формулы получим выражение для напряжения: σ = Muy/Jz Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии σmax = Muy max/Jz Отношение Jz/ymax называется моментом сопротивления сечения при изгибе и обозначается через Wх : Wх = Jz/ymax Таким образом, σmax = Mu/ Wх Эта формула является основной при расчете на прочность бруса при изгибе. Для бруса прямоугольного сечения Jz = bh3/12 Для бруса круглого сечения Jz = πD4/64 43. Напряжение в брусе при поперечном изгибе В случае поперечного изгиба в сечение бруса возникает не только изгибающий момент , но и поперечная сила Q. Эта сила представляет собой равнодействующую элементарных распределенных сил, лежащих в плоскости сечения . Следовательно , в этом случае в поперечных сечениях бруса возникают не только нормальные , но и касательные напряжения. Касательные напряжения τ сопровождаются появлением угловых деформаций γ. τ = G* γ G – модуль упругости 2-го рода. Поэтому , кроме основных смещений , свойственных чистому изгибу , получаются некоторые дополнительные угловые смещения, обусловленные сдвигом. При поперечном изгибе в отличие от чистого изгиба поперечные сечения бруса не остаются плоскими, они искривляются. Однако на величине нормальных напряжений искажение плоскости поперечных сечений заметным образом не скажутся.(Поперечная сила Q не меняется по длине бруса) Формулы для чистого изгиба , будут давать совершенно точные результаты и в случае поперечного изгиба. σ = Muy/Jz Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии σmax = Muy max/Jz Отношение Jz/ymax называется моментом сопротивления сечения при изгибе и обозначается через Wх : Wх = Jz/ymax Таким образом, σmax = Mu/ Wх Эта формула является основной при расчете на прочность бруса при поперечном изгибе. Для бруса прямоугольного сечения Jz = bh3/12 Для бруса круглого сечения Jz = πD4/64 Формулы для чистого изгиба дают некоторую погрешность h/l по сравнению с единицей, Где h – размер поперечного сечения в плоскости изгиба, L - длина бруса 44. Аналитический метод определения перемещений в балке при изгибе. Дифференциальное уравнение упругой линии. Вычисление прогибов и углов поворотов сечений. Наиболее типичной схемой нагружения является изгиб балки , расположенной на двух опорах , под действием внешней поперечной сосредоточенной силы , лежащей в одной из главных плоскостей инерции поперечного сечения балки. 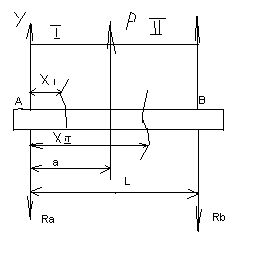 При изгибе балки происходит искривление ее оси в плоскости действия внешней силы. Искривленная ось балки может описываться уравнением в дифференциальной форме , которое называется уравнением упругой линии балки и имеет общий вид:± EJ (d2y/dx2) = M или ± EJ y″= M Где Е – модуль упругости первого рода , Y - перемещение сечения балки, Jz = bh3/12 - экваториальный момент инерции сечения балки относительно оси z. М – изгибающий момент в сечении. y' = dy/ dx = tg θ где θ - угол поворота сечения балки при нагружении изгибающей нагрузкой . Ввиду малости прогиба по сравнению с длинновыми размерами балки можно принять tg θ = θ Уравнение прогибов сечений : Для первого участка : EJY = - F(L-a)x13/6L + Fa(L-a)(2L-a)/6L; Для второго участка EJY = - F(L-a)x23/6L +F(x2-a)3/6+ Fa(L-a)(2L-a)/6L; Полученные зависимости позволяют определить прогибы и на консольном участке балки. Преимущество аналитического метода- высокая точность расчетов ,а недостаток – сложность и громоздкость. 45. Потенциальная энергия бруса в общем случае нагружения. Общий случай нагружения бруса , когда в поперечных сечениях возникают нормальные и поперечные силы , изгибающие и крутящие моменты одновременно . При разгрузке тела за счет потенциальной энергии производится работа. Упругое тело является аккумулятором энергии. Работа силы на упругом перемещении определяется половиной произведения наибольшего значения силы и перемещения ΔL . U = ½ P ΔL Если бы между силой и перемещением не было прямой пропорциональности, вместо коэффициента ½ был бы получен какой –то другой коэффициент. В частности при постоянной силе он равен единице. Исключая из полученного для U выражения ΔL, найдем U = P2l/2EF; Энергия упругих деформаций стержня при изгибе определяется работой момента М на взаимном угловом перемещении dθ двух сечений. dU = ½ M dθ dθ = dz/ρ = Mdz/EJx Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка dU = N2 dz /2EF, а для всего стержня U = L0∫ N2 dz /2EF. Энергетическое соотношение широко используется при определении перемещения в сложных упругих системах. 46. Определение перемещения бруса способом Верещагина Правило Верещагина - графоаналитический прием вычисления интегралов . Заключается в замене операций интегрирования перемножением площади эпюры моментов от внешней нагрузки Sf на ординату у0 линейной эпюры моментов от единичной силы F0 , расположенную под центром тяжести площади первой эпюры, т. е. интеграл Мора L0∫ MfM0dx = SfY0 или L0∫ MfM0dx = i=1∑n SfiY0i ; Перемещение в заданной точке изогнутой балки у = 1/EJz* L0∫ MfM0dx Метод Верещагина зависит от точности замеров , ошибка может составлять до ± 3%. Данный метод намного проще и удобнее аналитического , но погрешности в в измерениях и смещение точки приложения силы может повлиять на точность подсчетов. 47. Напряженные состояния в точках тела . Главные площадки и главные напряжения . Виды напряженного состояния. Материалы находящиеся под растяжением – сжатием над 2 –м или трем осям системы координат , имеет место сложное напряженное состояние . При исследовании растяжений тела , напряженность состояния описывалась 2-мя видами напряжений . Установили различные соотношения этих растяжений , которые зависят от угла наклона площади поперечного сечения. Площадки ,на которых касательные напряжения =0, называются главными , а напряжения на этих площадках главными напряжениями. Согласно точной теории упругости для общего случая напряженного состояния в точке, имеет место 3-и главных взаимноперпендик-ных площадки, через которые передаются главные напряжения. Главные напряжения σ1 > σ2 > σ3 Существует 3 –и вида напряженных состояния : 1) σ1≠ 0, σ2,3=0 Осевое простое напряженное состояние (при растяжении) 2 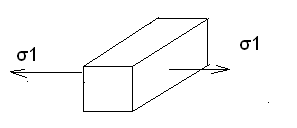 ) σ1,2≠ 0, σ3=0Плоское напряженное состояние 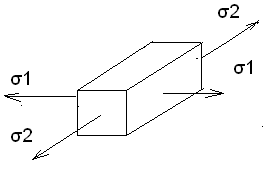 3) σ1,2,3≠ 0Объемное ,напряженное состояние 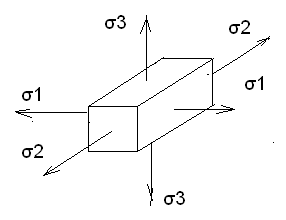 48. Деформация бруса при объемном ,напряженном состоянии. Обобщенный закон Гука. Рассматривается элементарный объем вокруг какой либо точки тела, при исследовании прочности в данной точке необходимо знать не только главное напряжение σ1,2,3, но и деформацию в этой точке. Изменение формы тела всегда связано с перемещением этих точек тела. Рассмотрим деформацию по осям 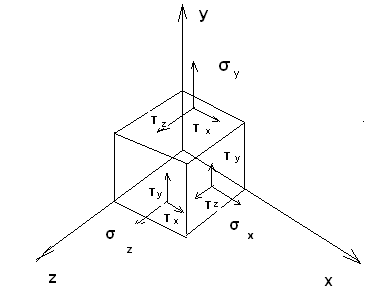 εx = σ1/E - μ σ2/E - μ σ3/E εy = σ2/E - μ σ1/E - μ σ3/E (1)(все уравнения) εz = σ3/E - μ σ1/E - μ σ2/E Аналитическое выражение закона Гука. Исследование (1) приводит к зависимости объемной деформации и главных напряжений. Сумма слева – относительная объемная деф-я. Относительное изменение объема e = εx+ εy+ εz V0 = 1 V = (1+ εx)* (1+ εy)* (1+ εz) V = 1 + εx+ εy+ εz Используется для сложного напряженного состояния. 49. Теории (гипотезы) прочности и их назначение . Понятие о эквивалентных напряжениях . Содержание и области применения теории прочности. Теории предельных напряжений .Гипотезы прочности. Задачи теории прочности: Оценить прочность детали находящейся в сложном напряженном состоянии через хорошо известное простое напряженное состояние. В каждой теории используются свои критерии расчета. 1) Теория наибольших нормальных напряжений. Если в какой –либо точке тела, в каком –либо направление нормальное напряжение достигает МАХ значение- происходит разрушения.(простые конструкции, сложные материалы) Галлелеу σмах<=[ σ] 2) Теория наибольших линейных деформаций Разрушение материалов рассматривают с точки зрения молекулярной теории. Происходит разрушение молекулярных сил, изменяется расстояние между молекулами. Разрушение в каждой точке произойдет если критические деформации будут близки к предельным. ε<= [ε] σ1 - μ σ2 - μ σ3 <= [σ] σэкв<=[ σ] Эквивалентное напряжение – напряжение, которое необходимо создать в растянутом стержне, чтобы его простейшее состояние было равно опасному сложному состоянию напряженного тела. (твердые материалы, расчет простых деталей) 3) Теория наибольших касательных напряжений Пластические деформации , которые в какой –либо точке достигнут произойдет разрушение. Условие прочности τmax <=[ τ] σ1 - σ3 <= [σ] Для плоско напряженного состояния получена зависимость σэкв= √( σ2 + 4 τ2)<=[ σ] 4) Энергетическая теория прочности Согласно этой теории на разрушение материала затрачивается не вся потенциальная энергия, а только часть , идущая на формообразование тела. Uф<= [Uф] Для плосконапряженного состояния получена зависимость. Используется при статических расчетах на прочность . Для пластичных материалов. 5) Теория Мора Согласно этой теории единого критерия оценки прочности при различных напряженных состояниях нет. Разрушение материала зависит от величины и знака наибольшего и наименьшего главных напряжений. Условие прочности σ1 – k*σ3 <= [σ] k – коэф-т учитывающий разные свойства материала при напряжение сжатии. K = [ σр]/ [ σс] 50. Сложное сопротивление бруса. Расчеты на прочность при косом изгибе. На тело действует несколько видов нагружений. Разложим сложный вид на простые составляющие. Частный случай :сочетание изгиба с растяжением. 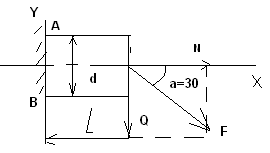 σ∑ = σN ± σM = N/S ± Ql/Wz = Fcosα/S ± Fsinα/Wz σ∑ = σN +σM <=[ σ] Косой изгиб – действие момента не совпадает с прямой осью. 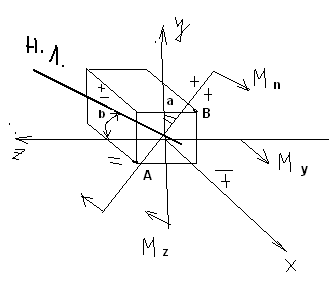 σz =± σMy ± σMz =± Mu*cosα /Wz ± Mu*sin α /Wy 51. Понятие об усталостной прочности. Основные характеристики цикла переменных напряжений. Усталостное разрушение связано с действием переменных напряжений. Усталость начинается с появлением микротрещин на поверхности детали. Микротрещина под действием напряжения увелич-ся и происходит внутр-е разрушение. В плоскости разрушения различают 2 характерных зоны. 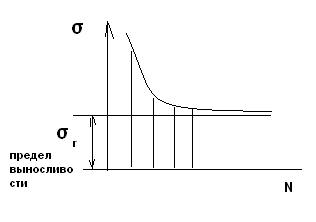  N – число циклов нагружений   R = σmin / σmax - чувствительность материала к симметрии тела.  σ-1 = σr Предел выносливости – такое направление, при котором материал выдерживает теоретически бесконечное число циклов нагружений.τ-1= σ-1/2 52. Прочность при перемещенных напряжениях. Усталостные разрушения связаны с действием переменных напряжений. Характер разрушений при усталости: усталостные разрушения появляются с возникновением микротрещин. Она увеличивается под действием переменных напряжений и происходит внезапное разрушение. В плоскости разрушения различают 2 характерные зоны: 1. зона наклона 2. зона внезапного разрушения. Предел выносливости  , N – число циклов, r – чувствительность материала при симметрии циклов |