кп. 1 часть. Виды нагружения. Напряжение, основные понятия. Реальный объект
 Скачать 2.61 Mb.
|
|
20.Косой изгиб Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения. Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как одновременный изгиб в 2-х плоскостях zx и zy. Для этого изгибающий момент Мизг раскладывается на составляющие моменты осей х и у. Мх=Мизгsin a, Му=Мизг cos a Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов Mx и My: Сигма= Мизг((у/Jx)sin a + (x/Jy)cos a) a - угол отклонения плоскости действия M от вертикали. Если в каждой точке сечения отложить по нормали вектор сигма, то концы векторов, как и при простом изгибе образуют плоскость. Уравнение нейтральной линии в сечении найдем, полагая сигма=0: У=-х(Jx/Jy) ctg a При косом изгибе нейтральная линия не перпендикулярна к плоскости изгибающего момента. 21.Изгиб и растяжение (сжатие) На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие. Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами. Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р. 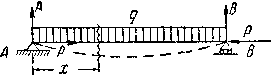 Рис.1 Совместное действие изгиба и сжатия. Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки. Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений,вызванных силами Р и нагрузкой q. Сжимающие напряжения  от сил Р равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений: нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой  Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно  22. Сложное сопротивление. Общие понятия, назначение. Косой изгиб. Изгиб с кручением Ранее были рассмотрены виды нагружения, при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор: нормальная сила N - при растяжении, изгибающий момент Мх - при чистом изгибе, крутящий момент Мк - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми. Кроме простых видов нагружения бывают и сложные виды нагружения или иначе сложное сопротивление. Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов. Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления: - косой изгиб; -внецентренное растяжение; -изгиб с кручением. При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения. 23. Усталостная прочность. Общие понятия, назначение. Параметры циклов нагружения Усталостная прочность - это прочность материала при циклическом нагружении. Усталостная прочность измеряется как и напряжение в [MПa]. Усталостная прочность обычно меньше в два или более раз чем предел прочности. Частота нагружения. На воздухе частотные зависимости пороговой интенсивности напряжений различных материалов неоднозначны. При этом линейная зависимость параметра от частоты сохраняется для всех исследуемых форм циклов напряжений. Влияние повышенной температуры испытаний. Характерной особенностью роста усталостной трещины при повышенных температурах является независимость порогового размаха коэффициента интенсивности напряжения от температуры испытаний в условиях нагружения с высокой асимметрией цикла напряжений. Циклом напряжений называется совокупность всех последовательных значений переменных напряжений за один период процесса их изменения. Параметры циклов:Наибольшее (в алгебраическом смысле) напряжение цикла называется максимальным и обозначается  (или  если рассматривается изменение касательных напряжений), а наименьшее – минимальным  (или  ).Амплитудой (или переменной составляющей) называется алгебраическая полуразность максимального и минимального напряжений цикла  . Амплитуда цикла всегда положительна.Цикл называют симметричным если напряжения  и  равны друг другу по абсолютной величине и обратны по знаку.Цикл называют асимметричным если напряжения и не равны друг другу по абсолютной величине.24. Усталостная прочность. Общие понятия, назначение. Предел выносливости при симметричном цикле Усталостная прочность - это прочность материала при циклическом нагружении. Усталостная прочность измеряется как и напряжение в [MПa]. Усталостная прочность обычно меньше в два или более раз чем предел прочности.Способность материала воспринимать многократное действие переменных напряжениях называют выносливостью. Расчетом на выносливость (или расчетом на усталостную прочность) называют проверку прочности элементов конструкции при многократном действии переменных напряжений. На рисунке сигмаr-предел выносливости, N-число циклов r-чувствительность материалов при симметрии циклов r=сигмаmin/сигмаmax По данным опытов получают так называемую кривую усталости (выносливости). соответствующую симметричным циклам (R = – 1). Аналогично могут быть получены кривые усталости, соответствующие циклам с другими значениями коэффициента асимметрии R. Разрушение материала при однократном нагружении происходит в тот момент, когда возникающие в нем напряжения равны пределу прочности  . Следовательно, кривые усталости при N = 1 имеют ординаты  равные .Кривая выносливости показывает, что с увеличением числа циклов уменьшается максимальное напряжение, при котором происходит разрушение материала. Наибольшее (предельное) максимальное напряжение цикла, при котором не происходит усталостного разрушения образца из данного материала после произвольно большого числа циклов, называют пределом выносливости. 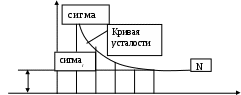 Таким образом, предел выносливости равен ординате асимптоты кривой усталости. Его обозначают  при симметричном цикле коэффициент асимметрии R = – 1 и предел выносливости при этом цикле обозначают  .25. Усталость. Факторы, влияющие на предел усталости. Общие понятия, назначение Процесс постепенного накопления повреждения материала при действии повторно-переменных напряжений, приводящий к образованию трещин и разрушению, называется усталостью материала. При переменных напряжениях поверхности развивающихся трещин многократно трутся друг о друга, в результате чего они шлифуются. Поэтому поверхность излома при усталостном разрушении состоит из двух зон: одна из них имеет нормальную для металла зернистую структуру, а другая – шлифованную поверхность. Усталостное разрушение детали происходит всегда внезапно (как разрушается хрупкий материал при статическом действии нагрузки) независимо от того, является металл хрупким или пластичным. Обычно считается, что изменение напряжений происходит по периодическому закону, например, по синусоидальному. Однако, экспериментально установлено, что вид этой кривой не имеет значения, прочность материала при переменных напряжениях зависит в основном от наибольшего и наименьшего напряжений. Факторы, влияющие на предел выносливости на предел выносливости: 1)концентраторы напряжений-связаны с констр-ой формой детали: источники появления микротрещин.Учитывается коэффициент концентрации, который представляет собой отношение предела выносливости лабораторного образца к пределу выносливости какой-то действ-ой формы детали Ксигма=(сигма -1)/(сигма -1)0>1 2)состояние повер-ти а)шлифование б)токарная обработка в)часовая токарная обработка KF=(сигма -1)d/(сигма -1)0 <1 –коэффициент состояния 3)масштаб Габаритный фактор Kd=(сигма -1)d/(сигма -1)0 <1 K -1=Kсигма/ KF Kd – коэффициент детали (сигма -1)d – действ-ый преедл выносливости (сигма -1)d= (сигма -1)/k –1 26. Усталость. Общие понятия, назначение. Расчет на прочность при переменных напряжениях Процесс постепенного накопления повреждения материала при действии повторно-переменных напряжений, приводящий к образованию трещин и разрушению, называется усталостью материала. При переменных напряжениях поверхности развивающихся трещин многократно трутся друг о друга, в результате чего они шлифуются. Поэтому поверхность излома при усталостном разрушении состоит из двух зон: одна из них имеет нормальную для металла зернистую структуру, а другая – шлифованную поверхность. Усталостное разрушение детали происходит всегда внезапно (как разрушается хрупкий материал при статическом действии нагрузки) независимо от того, является металл хрупким или пластичным. Расчет на прочность при переменных напряжениях расчет элемента конст-ции, находящейся под давлением переменных напряжений, начинается со статического расчета конструкции, целью кот-го является определение размеров при заданной нагрузке. Конструир-ие констр-ции - уточнение ее формы.Только после этого проводится уточненный проверочный расчет на усталость, в рез-те определяем кофф-т запаса прочности. Опред-ют коэфф-нт запаса при симметричной нагрузке при изгибе Коэффициент запаса прочности представляет собой отношение предела выносливости, определенного для детали, к номинальному значению максимального напряжения, возникающего в опасной точке детали.при изгибе при кручении 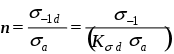 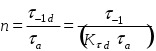 При несимметричных циклах нагружения формулы для определения коэффициентов запаса прочности по усталостному разрушению имеют вид: при изгибе  ,  при кручении , где  ,  .Наряду с коэффициентом запаса по усталостному разрушению должен быть определен коэффициент запаса по текучести. При изгибе (или при растяжении-сжатии)  , (I.12.6)при кручении  . (I.12.7)При работе бруса на совместное действие изгиба с кручением, когда в опасной точке детали возникает плоское напряженное состояние, общий коэффициент запаса прочности определяется из выражения  ≥[n]=1,5…3Здесь п - общий коэффициент запаса прочности;  - коэффициент запаса прочности по нормальным напряжениям; - коэффициент запаса прочности по касательным напряжениям.27. Реальный объект и его схема. Схематизация свойства материала, формы элементов конструкций нагрузок В сопротивлении материалов, как и во всякой отрасли естествознания, исследование вопроса о надежности реального объекта начинается с выбора расчетной схемы. Расчетная схема – отбрасывание от реального объекта его несущественных свойств. Схематизация состоит из 3-х видов допущений: схем-ция материала констр-ций. Допускают, что материал – однородный, сплошной изотроп. Схем-ция нагрузки. Ее харак-ют: а)сосредоточенная нагрузка (приложенная в точке) б)распределенная в)статическая-такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. г)динамическая- изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию (например, ударные). 3)схем-ция формы конструкции (сущ-ют 2 основные формы: брус и оболочка) Брус- это геом-ое тело, одно из измерений которого много больше 2-х других Оболочка – это геом-ое тело, одно из измерений которого много меньше 2-х других. 28. Внешние и внутренние силы. Применение метода сечения для определения внутренних сил и напряжений Под внешними силами понимаются силы, возникающие в результате взаимодействия рассматриваемого тела с окружающими телами. Внутри любого материала имеются внутренние межатомные силы. Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) их, т.е. появление дополнительных внутренних сил. Дополнительные силы взаимодействия, возникающие внутри объекта под действием внешних сил, называются в сопротивлении материалов внутренними силами.Для определения внутренних усилий используется метод сечений.  Сущность метода заключается в следующем. Пусть некоторое тело находится в равновесии под действием системы внешних сил Рассечем (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением). Отбросим правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы. Заменим действие одной части на другую внутренними силами. Эти внутренние силы по характеру приложения - распределенные, в общем случае они не одинаковы по всему сечению. N - продольная (нормальная) сила, проекция вектора R на ось z; Qx, Qy- поперечные силы, проекции вектора R на оси x,y соответственно; Mz=Mк - крутящий момент, составляющая момента M вокруг оси z; Mx, My- изгибающие моменты, составляющие момента M вокруг осей x, yсоответственно. |