лекция изгиб. Плоский прямой изгиб
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
5.ПЛОСКИЙ ПРЯМОЙ ИЗГИБ 5.17. Поперечная сила, изгибающий момент и их эпюры 5.18. Напряжения в поперечном сечении балки 5.19. Расчет балок на прочность 5.20. Перемещения при изгибе. Расчет балок на жесткость 5.17. Внутренние усилия в поперечных сечениях бруса Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях бруса возникают изгибающие моменты Mx или My . Если изгибающий момент в сечении является единственным силовым фактором, то изгиб называется чистым (рис. 5.1, а).  Рис. 5.1 В тех случаях, когда в поперечных сечениях бруса наряду с изгибающим моментом возникают и поперечные силы изгиб называется поперечным. Брус, работающий в основном на изгиб, часто называют балкой. В дальнейшем будем рассматривать такие случаи изгиба балки, при которых, вопервых, поперечное сечение балки имеет хотя бы одну ось симметрии, и, вовторых, вся нагрузка лежит в плоскости, совпадающей с осью симметрии балки. Таким образом, одна из главных осей инерции лежит в плоскости изгиба, а другая перпендикулярна ей. Для того, чтобы правильно ориентироваться в вопросах, связанных с расчетом бруса на изгиб, необходимо прежде всего научиться определять законы изменения внутренних силовых факторов, т.е. научиться строить эпюры изгибающих моментов и поперечных сил. Предварительно рассмотрим три основных типа опорных связей балки с основанием: 1. Шарнирноподвижная опора (рис. 5.1, б левая опора балки), ограничивающая лишь вертикальное перемещение опорного узла. 2. Шарнирнонеподвижная опора (рис. 5.1, б правая опора балки), ограничивающая вертикальное и горизонтальное перемещения опоры. 3. Жесткая заделка (рис. 5.1, а опора балки на левом краю), не допускающая поворота и перемещений по вертикали и горизонтали сечения балки, примыкающего к опоре. По запрещенным направлениям во всех этих типах опор возникают соответствующие реакции. Рассмотрим характерный пример (рис. 5.2, а) и установим необходимые правила. Решение задачи, как правило, начинается с определения полной системы внешних сил. Для этого отбросим опоры и заменим их соответствующими реакциями (рис. 5.2, б), выполняющими ту же роль, что и опорные закрепления.  Рис. 5.2 Заданная система статически определима, следовательно, из условий равновесия системы, т.е. равенства нулю суммы моментов всех сил относительно шарнирных опор (в шарнирах нет ограничений поворота сечений балки, поэтому изгибающих моментов не возникает) m(A) = 0 и m(В) = 0, определяем вертикальные реакции в опорах: 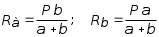 . (5.1) . (5.1)Для определения НА имеем: 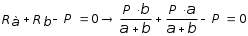 , 0 = 0. , 0 = 0.Для определения внутренних силовых факторов изгибающего момента М(z) и поперечной силы Q(z) как функций от продольной координаты z, воспользуемся методом сечений. Для получения этих зависимостей балку разбивают на участки, границами которых являются следующие точки: начало и конец балки; точки приложения сосредоточенных усилий; начало и конец действия распределенных усилий; сечения, в которых скачкообразно изменяется жесткость балки; в точках, где происходит изменение ориентации элементов, если имеем дело с стержневой системой со сложной структурой.  Рис. 5.3 Заданная система состоит из двух участков первого (0 z a) и второго (a z a + b). Следовательно, задавая последовательно сечения, принадлежащие к первому и второму участкам, и рассматривая равновесие отсеченных частей системы при действии на них всех внешних сил и внутренних усилий, определим выражения для внутренних силовых факторов. При этом, знак изгибающего момента устанавливается по знаку кривизны изогнутого бруса (рис. 5.3, а) и зависит от выбранного направления осей системы координат y0z. Следовательно, в системе координат y0z принятой на рис. 5.3, а положительный момент вызывает растяжение нижних волокон балки. Для поперечных сил, независимо от направления координатных осей, устанавливается следующее правило знаков: если результирующая поперечная сила Qy вращает рассматриваемую часть балки по ходу часовой стрелки, то она считается положительной, в обратном случае отрицательной (рис. 5.3, б). Из условия равновесия Mx = 0; y = 0 отсеченной части системы, расположенной левее от сечения z1 (первый участок), (см. рис. 5.2, в), получим: Mx (z1) = Ra z1; Qy = Ra . (5.2) Для определения Mx и Qy на втором участке рассмотрим равновесие отсеченной части балки, расположенной правее от сечения z2 (см. рис. 5.2, б), т.е. Mx = 0; y = 0 откуда и определим: Mx (z2) = Rb (a + b z2); Qy = Rb . (5.3) Эпюры Mx и Qy изображены на рис. 5.4. Заметим, что эпюры изгибающих моментов Mx , как и поперечных сил Qy строятся на оси бруса, однако в отличие от эпюры поперечных сил знак момента не указывается, а ординаты изгибающего момента откладываются co стороны растянутых волокон. 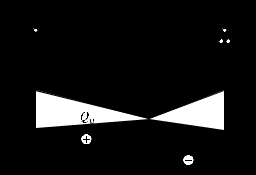 Рис. 5.4 Основные дифференциальные соотношения теории изгиба Пусть брус нагружен произвольным образом распределенной нагрузкой q = f (z) (рис. 5.5, а).  Рис. 5.5 Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 5.5, б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, проходящей через точку С (рис. 5.5, б), получим: Qy + q dz Qy d Qy = 0 ; Mx + Qy dz + q dzdz/2 Mx d Mx = 0. Производя упрощения и отбрасывая величины высшего порядка малости, получим: 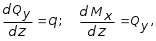 (5.4) (5.4)откуда 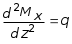 . (5.5) . (5.5)Из (5.4) следует, что при q = const функция Qy будет линейной, а функция Mx квадратичной. Если на какихто участках бруса распределенная нагрузка отсутствует, т.е. q = 0, то получим, что Qy = const, а Mx является линейной функцией от z. В сечениях, где приложена сосредоточенная сила, эпюра Qy претерпевает скачок на величину внешней силы. И наконец, в тех сечениях, где Qy принимает нулевое значение и меняет знак, функция Mx достигает экстремальных значений. 5.18. Напряжения при чистом изгибе Рассмотрим наиболее простой случай изгиба, называемый чистым изгибом. Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а поперечные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, согласно второго выражения (5.4), вдоль продольной оси z принимает постоянное значение. Так как в любом сечении стержня при чистом изгибе Mx(z) = const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих моментов ось бруса искривляется. Исходя из этого, ось бруса принимает форму дуги окружности с радиусом кривизны (рис. 5.6). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба переместятся в пространстве таким образом, что их совокупность снова образует плоскость. Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сечений друг относительно друга. Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии dz (рис. 5.6). В результате изгиба эти сечения наклонятся, образуя между собой угол d, в связи с чем верхние волокна удлиняются, а нижние укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом CD = CD= dz = d. Произвольный отрезок АВ, расположенный от СD на расстоянии y, в результате изгиба удлинится на величину AB AB. С учетом построений, изображенных на рис. 5.6, легко определить величину его линейной деформации: 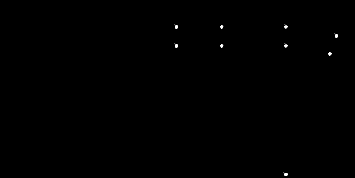 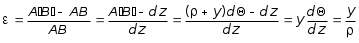 . (5.6) . (5.6)Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения сжатия. Тогда переход от деформаций к нормальным напряжениям можно осуществить посредством закона Гука: 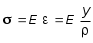 (5.7) (5.7)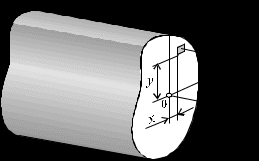 Рис. 5.7 Установим положение нейтральной оси x, от которой происходит отсчет координаты у (рис. 5.7). Учитывая, что сумма элементарных сил dF по площади поперечного сечения F дает нормальную силу Nz . Но при чистом изгибе Nz = 0, следовательно: 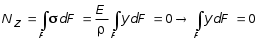 . .Как известно, последний интеграл представляет собой статический момент сечения относительно нейтральной линии (оси x). Статический момент равен нулю, значит, нейтральная линия проходит через центр тяжести сечения. Выразим момент внутренних сил относительно нейтральной оси Mx через . Очевидно, что C учетом выражения (5.7) получим: 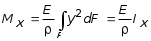 . . Откуда 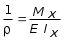 , (5.9) , (5.9)где Из формулы (5.7), исключая 1/, окончательно получим: 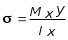 . (5.10) . (5.10)Откуда следует, что нормальные напряжения в поперечном сечении бруса при его изгибе изменяются по линейному закону в зависимости от координаты y и принимают максимальное значение на уровне крайних волокон (при y = ymax): 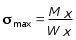 , ,где 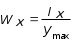 момент сопротивления сечения. момент сопротивления сечения.Энергия упругих деформаций бруса при изгибе V определяется работой момента Mx на соответствующем угловом перемещении d: 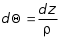 и и 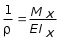 , ,окончательно получим 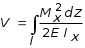 . (5.11) . (5.11)5.19. Примеры расчетов Для статически определимых систем: схемы I (консольная балка, рис. 5.8, а), схемы II (двухопорная балка с консолями, рис. 5.13) и схемы III (плоской рамы в виде ломаного бруса, рис. 5.17) при последовательном их рассмотрении требуется: 1. Построить эпюры Mx и Qy для всех схем и эпюру Nz для схемы III; 2. Руководствуясь эпюрой Mx , показать на схемах I и II приблизительный вид изогнутой оси балки. По опасному сечению подобрать размеры поперечного сечения: а) для схемы I прямоугольное hb при расчетном сопротивлении RH = 16103 кН/м2 (клееная древесина); h:b = 1,5; б) для схемы II двутавровое (ГОСТ 823972) при расчетном сопротивлении RH = 200103 кН/м2 (сталь); Решение 5.19.1. Схема I. Консольная балка (задача №6) Учитывая особенности рассматриваемой системы (рис. 5.8, а), чтобы исключить необходимость определения опорных реакций, достаточно применяя метод сечений, последовательно рассмотреть те отсеченные части системы от заданного сечения, в котором отсутствует опорное сечение. Построить эпюры Qy и Mx. Для построения эпюр Qy и Mx определяем количество участков, затем, используя метод сечений, составляем аналитические выражения изменения Qy и Mx в зависимости от текущей абсциссы z для каждого участка.  Рис. 5.8 Определение количества участков балки Границами между двумя смежными участками, как правило, являются места расположения тех сечений, где происходит скачкообразное изменение: физико-механических характеристик материала конструкций; геометрических характеристик поперечных сечений (формы и/или размеров), а также внешних нагрузок. В данном случае, рассматриваемая балка, имеющая постоянное поперечное сечение (рис. 5.8, б) имеет три участка: участок I DС, участок II СВ, участок III ВА. Составление аналитических выражений Qy и Mx и определение значений в характерных сечениях Проведя сечение II, рассмотрим равновесие правой отсеченной части балки длиной z1, приложив к ней все действующие справа от сечения заданные нагрузки и внутренние силовые факторы Qy и Mx , возникающие в сечении, которые заменяют действие отброшенной части балки (рис. 5.9). При этом, предполагаем, что изображенные на рисунке внутренние силовые факторы положительны. Составив уравнения равновесия y = 0 и 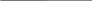 y = 0, y = 0, Полученные выражения показывают, что на участке I  Участок II (1 м z2 2 м). Составим уравнения y = 0 и y = 0, Из полученных выражений для Теперь, подставляя значения z2 для характерных сечений участка II в полученные аналитические выражения, определим величины при z2 = 1 м; при z2 = 2 м; Участок III (2 м z2 4 м). Составим уравнения равновесия y = 0 и y = 0, 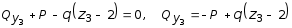 ; ;Таким образом, величина  Рис. 5.11 Подставив значения z3 , соответствующие характерным сечениям участка, в аналитические выражения изменения При z3 = 2 м При z3 = 4 м Так как, поперечная сила в пределах участка меняет знак, т.е. имеет промежуточное нулевое значение (рис. 5.8, в), то в этом сечении возникает экстремальное значение изгибающего момента. Для определения его величины вначале найдем значение z0 , при котором P + q (z0 2) = 0, 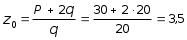 м. м.Подставив найденное значение z0 = 3,5 м в аналитическое выражение изменения Построение эпюр Qy и Mx для всей балки Отложив перпендикулярно к оси абсцисс (линии, параллельной оси балки) в удобном для пользования масштабе вычисленные значения Qy и Mx в характерных и промежуточных сечениях каждого участка и соединяя концы полученных ординат линиями, соответствующими законам изменения Qy и Mx на каждом участке, построим эпюры Qy и Mx для всей балки (рис. 5.8, в, г). При этом положительные ординаты эпюры Qy откладываются вверх, а отрицательные вниз по оси абсцисс. Ординаты же эпюр Mx откладываются со стороны растянутого волокна. На эпюрах Qy обязательно указываются знаки, а на эпюре Mx знаки можно не ставить. Проверка правильности построения эпюр Qy и Mx  Рис. 5.12 Для этого необходимо вначале проверить соответствие эпюры Qy эпюре Mx согласно дифференциальной зависимости 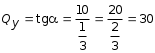 кН. кН.При этом, знак поперечной силы будет положительным, если угол образован вращением оси балки или элемента системы по ходу часовой стрелки, и отрицательным, если угол образован вращением этой оси против часовой стрелки до совмещения с эпюрой Mx . В рассматриваемом примере угол образован вращением оси балки против часовой стрелки, поэтому поперечная сила на этом участке будет отрицательной. После указанной проверки полезно также проверить выполнение следующих положений: 1. Эпюра Mx на участке между сосредоточенными силами, а также между сосредоточенными силой и моментом, и между началом или концом действия равномерно распределенной нагрузки и сосредоточенными силой и моментом всегда изменяется по закону прямой линии, наклонной к оси элемента, а в пределах действия равномерно распределенной нагрузки по закону квадратной параболы, имеющей выпуклость в сторону ее действия, если эпюра построена со стороны растянутого волокна; 2. Под точкой приложения сосредоточенной силы эпюра Mx имеет излом, острие которого направлено в сторону действия силы, если эпюра построена со стороны растянутого волокна; 3. На эпюре Mx в месте действия сосредоточенного момента m имеет место скачок, равный его величине; 4. Над шарнирными опорами двухшарнирной балки изгибающий момент может быть только в тех случаях, когда в опорных сечениях приложены сосредоточенные моменты или когда на консолях, расположенных за опорами, приложены нагрузки. Во всех других случаях изгибающие моменты в шарнирах равны нулю; 5. На участке действия равномерно распределенной нагрузки изгибающий момент достигает экстремального значения Mx = = Mmax в том сечении, где поперечная сила 6. Поперечная сила Qy на участке равна нулю, если во всех сечениях по длине этого участка Mx = const; 7. Эпюра Qy постоянна на участках между сосредоточенными нагрузками и изменяется по закону наклонной прямой лишь на участках, где действует равномерно распределенная нагрузка; 8. Эпюра Qy в точках приложения сосредоточенных вертикальных сил (Р, RA , RB) имеет скачки, равные по величине приложенным в этих сечениях сосредоточенным силам, причем направление скачков всегда совпадает с направлением этих сил. В нашем примере все эти положения выполняются. 2.1. Руководствуясь эпюрой Mx, показать приблизительный вид изогнутой оси балки. При построении приблизительного вида изогнутой оси балки по эпюре Mx необходимо знать, что знак изгибающего момента связан с характером деформации балки от действия заданной внешней нагрузки. Если на участке балки изгибающий момент положителен, то балка на этом участке изгибается выпуклостью вниз, а если отрицателен выпуклостью вверх. В тех же сечениях, где изгибающий момент равен нулю, кривизна балки меняет свой знак, т.е. ось балки в этих сечениях имеет точки перегиба. При этом всегда следует помнить, что прогибы балки на опорах равны нулю. Анализируя эпюру Mx (рис. 5.8, г), видим, что на участке АО растянуты нижние волокна, значит, на этом участке изогнутая ось балки будет иметь выпуклость вниз. На участке ОД растянуты верхние волокна, поэтому изогнутая ось балки на этом участке будет иметь выпуклость вверх. Таким образом, под точкой О, где Mx = 0, кривизна изогнутой оси балки меняет знак, т.е. упругая линия имеет в этом сечении точку перегиба. Учитывая это, строим приблизительный вид изогнутой оси балки (рис. 5.8, д). 2.2. Подбор поперечного сечения балки. Опасным сечением является то, в котором возникает наибольший по абсолютной величине изгибающий момент. В нашем примере опасным является сечение Е, где Mmax = 42,5 кНм. Прямоугольное сечение балки из клееной древесины подбираем из условия прочности при расчетном сопротивлении RH = 16103 кН/м2 и соотношения h/b = 1,5: откуда требуемый момент сопротивления сечения балки при изгибе будет равен: Момент сопротивления прямоугольного сечения равен: 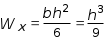 . .Приравняв его = 0,288 м, тогда: Округляя, принимаем брус поперечным сечением hb = 0,29 0,19 м2, (Wx = 2,66310-3м3). |
