лекция изгиб. Плоский прямой изгиб
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
5.19.2. Схема II. Двухопорная балка (задача № 7) 1.Построить эпюры Qy и Mx. Существенное отличие этой схемы (рис. 5.13, а) от предыдущего примера расчета (рис. 5.8, а) заключается в том, что при рассмотрении однопролетной консольной балки, для определения внутренних силовых факторов с применением метода сечений, мы последовательно рассматривали равновесие той части системы, где отсутствовало опорное сечение. Данное обстоятельство позволило без предварительного определения опорных реакций, вычислить значения внутренних усилий. Так как этот прием, в данном случае, нереализуем, поэтому предварительно необходимо определить полную систему внешних сил, которая включает заданную систему и все опорные реакции. Определение опорных реакций При общем случае нагружения в заданной системе возникают три опорные реакции. Однако, учитывая особенности характера нагружения, т.е. все внешние силы направлены по оси y, поэтому можно утверждать, что горизонтальная опорная реакция в опорном сечении А в данном случае равна нулю. Вертикальные опорные реакции могут быть определены из условий MA = 0; MB = 0. Необходимым и достаточным условием проверки правильности определения вертикальных опорных реакций является y = 0, т.к. это уравнение статики, применительно к рассматриваемой системе, которое содержит все искомые опорные реакции. Из MA = 0 получим: MA = Р1 + q54,5 m RB6 = 0, откуда Из уравнения MB = 0 будем иметь: MB = P7 m q51,5 + RA 6 =0; RA = 40 кН. Опорные реакции RA и RB получились положительными. Это означает, что выбранные направления совпадают с их действительными направлениями. После определения опорных реакций следует провести проверку правильности их вычисления.  Рис. 5.13 y = P q5 + RA + RB = 0; 10 205 + 40 + 70 = 0; 110 + 110 = 0; 0 = 0. Удовлетворение этого уравнения говорит о правильности вычисления величин и направления опорных реакций. Определение количества участков Учитывая, что границами участков являются точки приложения внешних сил и опорных реакций, а также сечения, где распределенная нагрузка меняется скачкообразно. Поэтому заданная балка имеет четыре участка: I участок КА; II участок АС; III участок СВ и IV участок ВD (рис. 5.13, б). Составление аналитических выражений Qy, Mx и определение значений их в характерных сечениях каждого участка Поместив начало системы координат в центре тяжести крайнего левого поперечного сечения балки, и рассекая ее в пределах участка I, рассмотрим равновесие левой части балки длиной z1 (рис. 5.14, а). Составив уравнения равновесия y = 0 и  Рис. 5.14 y = 0, Знак “минус” у при z1 = 0 при z1 = 1 м Проведя сечение в пределах участка II, рассмотрим равновесие левой отсеченной части балки (рис. 5.14, б) и из уравнений равновесия y = 0 и y = 0, Подставив в полученные выражения значения z2 , соответствующие граничным сечениям участка II, определим величины при z2 = 1 м при z2 = 3 м Сделав сечение в пределах участка III, составив и решив уравнения равновесия y = 0 и y = 0, 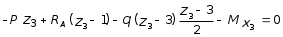 , ,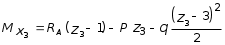 уравнение параболы. уравнение параболы. Рис. 5.15 Теперь найдем 20(3 3) = 30 кН, при z3 = 7 м Как видно, поперечная сила 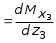 = 0, будет экстремальное значение изгибающего момента. Для его определения найдем величину z0 , при котором = 0, будет экстремальное значение изгибающего момента. Для его определения найдем величину z0 , при котором RA P q(z0 3) = 0, 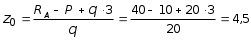 м. м.Подставив найденное значение z0 = 4,5 м в выражение для Для получения аналитических выражений изменения Qy и Mx на участке IV целесообразно начало координат перенести в сечение D и рассматривать равновесие правой отсеченной части, т.к. в этом случае вследствие меньшего количества внешних сил, приложенных к правой части балки, аналитические выражения будут проще по своему виду, а вычисление ординат менее трудоемко.  Рис. 5.16 Аналитические выражения y = 0, 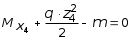 , , 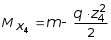 (парабола). (парабола).В граничных сечениях D и В участка IV ординаты эпюр Qy и Mx : при z4 = 0 при z4 = 1 м Так как величина Построение эпюр Qy и Mx для всей балки Откладывая перпендикулярно от оси абсцисс в удобном для пользования масштабе значения Qy и Mx , возникающие в характерных и промежуточных сечениях каждого участка, и соединяя концы полученных ординат линиями, соответствующими законам изменения Qy и Mx на этих участках, строим эпюры Qy и Mx для всей балки (рис. 5.13, в, г). 2.1. Руководствуясь эпюрой Mx показать приблизительный вид изогнутой оси балки. Анализируя эпюру Mx (рис. 5.13, г) видим, что на участке КО растянуты верхние волокна, и поэтому на этом участке изогнутая ось балки будет иметь выпуклость вверх. На участке ОD растянуты нижние волокна, и изогнутая ось балки будет иметь выпуклость вниз. Вследствие этого под т. О, где Mx = 0, будет точка перегиба. Учитывая все сказанное и то, что прогибы в опорных сечениях равны нулю, строим приблизительный вид изогнутой балки (рис. 5.13, д). 2.2. Подбор поперечного сечения балки. Опасным является сечение Е, где возникает наибольший по абсолютной величине Mmax = 72,5 кНм. Двутавровое сечение балки подбираем из условия прочности при изгибе при расчетном сопротивлении материала RH = 200103 кН/м2 (сталь): Откуда требуемый момент сопротивления Wx равен: По сортаменту (ГОСТ 823972) принимаем двутавр № 27 с Wx = 37,1105 м3. В этом случае при проверке прочности получается недонапряжение, но оно будет меньше 5, что допускается СНиП при практических расчетах. Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения. Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки строго говоря не остаются плоскими. Однако при 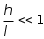 (где h высота поперечного сечения, l длина балки) оказывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плоских сечений и в случае чистого изгиба с достаточной точностью приемлема. Поэтому для расчета нормальных напряжений применяют ту же формулу (5.10). (где h высота поперечного сечения, l длина балки) оказывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плоских сечений и в случае чистого изгиба с достаточной точностью приемлема. Поэтому для расчета нормальных напряжений применяют ту же формулу (5.10). Рассмотрим вывод расчетных формул для касательных напряжений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной dz (рис. 5.21, а).  Рис. 5.21 Продольным горизонтальным сечением, проведенным на расстоянии y от нейтральной оси, разделим элемент на две части (рис. 5.21, в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности касательных напряжений, получим, что касательные напряжения в поперечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. 5.21, б). С учетом данного обстоятельства и из допущения о том, что касательные напряжения по площади bdz распределены равномерно, используя условие z = 0, получим: N N dN + bdz = 0 , откуда 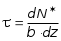 . (5.12) . (5.12)где N равнодействующая нормальных сил dF в левом поперечном сечении элемента dz в пределах заштрихованной площади F (рис. 5.20, г): С учетом (5.10) последнее выражение можно представить в виде 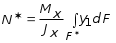 , (5.14) , (5.14)где 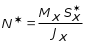 , ,откуда 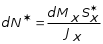 . (5.15) . (5.15)В результате совместного рассмотрения (5.12) и (5.15) получим 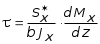 , ,или окончательно 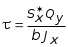 . (5.16) . (5.16)Полученная формула (5.16) носит имя русского ученого Д.И. Журавского. Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из состава балки вокруг исследуемой точки элементарную призму (рис. 5.21, г), таким образом, чтобы вертикальная площадка являлась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол относительно горизонта. Принимаем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси dz, т.е. по оси z; по вертикальной оси dy, т.е. по оси у; по оси х равный ширине балки. Так как вертикальная площадка выделенного элемента принадлежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения на этой площадке определяются по формуле (5.10), а касательные напряжения по формуле Д.И. Журавского (5.16). С учетом закона парности касательных напряжений, легко установить, что касательные напряжения на горизонтальной площадке также равны . Нормальные же напряжения на этой площадке равны нулю, согласно уже известной нам гипотезе теории изгиба о том, что продольные слои не оказывают давления друг на друга. Обозначим величины нормальных и касательных напряжений на наклонной площадке через и , соответственно. Принимая площадь наклонной площадки dF, для вертикальной и горизонтальной площадок будем иметь dF sin и dF cos , соответственно. Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 5.21, г), получим: откуда будем иметь: Следовательно, окончательные выражения напряжений на наклонной площадке принимают вид: 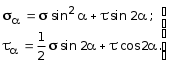 Определим ориентацию площадки, т.е. значение = 0 , при котором напряжение принимает экстремальное значение. Согласно правилу определения экстремумов функций из математического анализа, возьмем производную функции от и приравняем ее нулю: 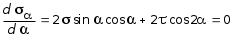 . .Предполагая = 0 , получим: Откуда окончательно будем иметь: Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называемых главными, а сами напряжения главными напряжениями. Сопоставляя выражения и 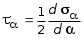 , ,откуда и следует, что касательные напряжения на главных площадках всегда равны нулю. В заключение, с учетом известных тригонометрических тождеств: 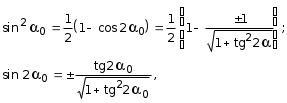 и формулы определим главные напряжения, выражая из через и : 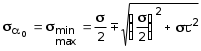 . .Полученное выражение имеет важное значение в теории прочности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу. Пример расчета (задача № 8) Для составной балки, имеющей поперечное сечение, показанное на рис. 5.22, требуется: 1. Определить расчетные параметры поперечного сечения балки; 2. Вычислить нормальные напряжения по заданному изгибающему моменту и построить их эпюру; 3. Определить значения касательных напряжений в точке 3; 4. Определить значения главных напряжений в точке 3 и указать их направления (показать главные площадки), имея в виду, что сечение относится к левой части балки. Дано: расчетные значения изгибающего момента и поперечной силы в сечении МP = 156 кНм, QP = 104 кН; hCT = 0,34 м; b1/hCT = 0,7; b2/hCT = 0,9; 1/hCT = 0,1; 2/hCT = 0,07; /1 = 0,4. Нормативное значение сопротивления материалу при изгибе RH = = 217100 кН/м2, коэффициент запаса по прочности n = 1,3. Решение 1. Определение расчетных параметров поперечного сечения балки (рис. 5.22, а). Ширина верхней полки b1 = = 0,7hCT = 0,70,34 = 0,238 м, принимаем b1 = 0,24 м; толщина верхней полки 1 = 0,1hCT = 0,10,34 = 0,034 м; площадь сечения верхней полки Определение площади поперечного сечения балки. Определение центра тяжести поперечного сечения балки. Ось y является осью симметрии сечения балки, следовательно, центр его тяжести находится на этой оси. За вспомогательную ось для определения координаты центра тяжести сечения на оси y принимаем ось x1 (рис. 5.22, а). Заметим, что поперечное сечение балки является составным, и включает в себя три прямоугольника (верхняя и нижняя полки, а также стенка). С учетом данного обстоятельства и воспользовавшись выражением (3.6), вычислим статический момент площади поперечного сечения балки относительно оси x1 : 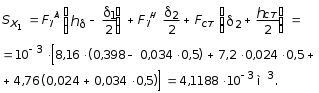 Тогда положение центра тяжести на оси у определится ординатой Определение момента инерции поперечного сечения балки относительно центральной оси (рис. 5.22). Значение момента инерции вычислим, пользуясь зависимостью между моментами инерции относительно параллельных осей: где 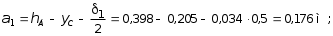 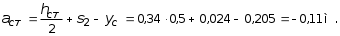 2. Вычислить нормальные напряжения по заданному изгибающему моменту и построить их эпюру. Момент сопротивления Wx для точек 1 и 2 определим по формулам: для точки 1 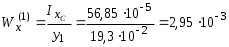 м3; м3;для точки 2 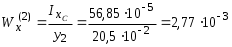 м3, м3,где y1 = h - yc = 0,398 0,205 = 0,193 м, y2 = yC = 0,205 м. Вычислим напряжения в точке 1 (рис. 5.22, а): 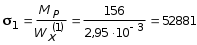 кН/м2 53000 МПа < 167000 кН/м2 кН/м2 53000 МПа < 167000 кН/м2 Вычислим напряжения в точке 2 (рис. 5.22, а): 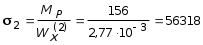 кН/м2 56000 МПа < 167000 кН/м2 кН/м2 56000 МПа < 167000 кН/м2Найдем значение нормальных напряжений в точке 3 по (5.10): 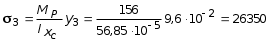 кН/м2 . кН/м2 .По полученным значениям строим эпюру нормальных напряжений (рис. 5.22, б). Проверку прочности производим по формуле где MP расчетный изгибающий момент; Wx момент сопротивления при изгибе; RИ допускаемое напряжение при изгибе. Допускаемое напряжение при изгибе равно: 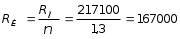 кН/м2. кН/м2.Как видно, балка имеет значительное недонапряжение. 3. Определить значения касательных напряжений в точке 3. Касательное напряжение определим по формуле Журавского: 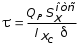 , ,где Вычислим статический момент отсеченной части в точке 3 части сечения + 0,00119(0,096 + 0,1250,34) = 1,54410-3 м3, где Вычислим касательное напряжение в точке 3:  4. Определить значения главных напряжений в т. 3 и указать их направления (показать главные площадки), имея в виду, что сечение относится к левой части балки. Главные напряжения в точке 3 определяем по формуле: 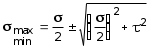 . .Подставив в данную формулу значения 3 и 3 , получим: 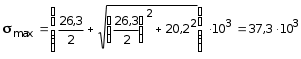 кН/м2; кН/м2;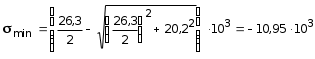 кН/м2. кН/м2.В заключение найдем положение главных площадок и направление главных напряжений (рис. 5.22, в). При отрицательном угле 0 откладываем его от нормали к сечению (площадке) по часовой стрелке и показываем положение главных площадок и направление главных напряжений (рис. 5.22). |
