лекция изгиб. Плоский прямой изгиб

• Название: Плоский прямой изгиб
• Анкор: лекция изгиб
• Дата: 23.03.2023
• Размер: 1.44 Mb.
• Имя файла: лекция изгиб.doc
• Тип: Документы; #1010264
• страница: 5 из 5

M_y = 0, M_y + P a  q b₁ z₃ = 0, M_y = q b₁ z₃ P a = 1,2 z₃  0,3.

Величина M_y определяется как линейная функция от z₃. При z₃ = 0; M_y = 0,3 кНм. В этом сечении растягивающие напряжения возникают не в дальней части сечений, а в ближней  ординату откладываем к наблюдателю.

При z₃ = 0,5м M_y = 1,20,5  0,3 = 0,60,3 = 0,3 кНм.

В этом сечении M_y откладываем от наблюдателя (рис. 5.35, г).

2.Установить вид сопротивления для каждого участка бруса. По эпюрам устанавливаем вид сопротивления на каждом участке бруса. На участке АВ возникают изгибающий момент M_y  и поперечная сила Q_x , что свидетельствует о наличии поперечного изгиба. На участке ВС возникают изгибающие момен­ты M_x, M_y , поперечные силы Q_x , Q_y  и крутящий момент M_x , что свидетельствует о наличии косого изгиба и кручения. На участке СD действуют изгибающие моменты M_x  и M_y , поперечная сила Q_x , растягивающая сила N и крутящий момент M_z , что свиде­тельствует о наличии косого изгиба с растяжением и кручением.

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N, M_x, M_y  и M_z (касательными напряжениями от Q_x  и Q_y  можно пренебречь). Участок АВ. Наибольшая величина изгибающего момента M_y , судя по эпюре (рис. 5.35, г) возникает в сечении, бесконечно близком к точке В. Максимальные нормаль­ные напряжения при изгибе определяются по формуле:

16,710³ кН/м²,

где момент сопротивления W_y  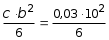= =1,810^-5 м³.

Участок ВС. По эпюрам M_x  и M_y  устанавливаем, что опасным является сечение, бесконечно близкое к точке С. Для круглого сечения суммарный изгибающий момент:

кНм,

а наибольшие нормальные напряжения равны:

кН/м²=33,32 МПа,

где момент сопротивления круглого сечения при изгибе: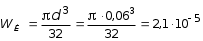

м³ .

При кручении круглого сечения возникают касательные на­пряжения, максимальные значения которых определяются по фор­муле: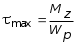

,

где W_p   момент сопротивления при кручении. Известно, что

W_p = 2 W_И = 22,110⁵ м³ = 4,210⁵ м³,

тогда

кПа=7,143 МПа.

Участок СD. По эпюрам M_x  и M_y  видим, что равными по опасности будут сечения, бесконечно близкие к точкам С и D. При действии растягивающей силы N во всех точках поперечного сече­ния возникают одинаковые нормальные напряжения:

кН/м² = 0,555 МПа,

где F = bc = 0,060,03=0,0018 м²  площадь поперечного сечения;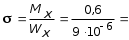

66666 кН/м² = 66,67 МПа,

где

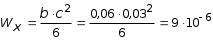м³.

При действии изгибающего момента M_y  наибольшие нормаль­ные напряжения будут равны: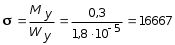

кН/м² = 16,67 МПа.

При кручении бруса прямоугольного сечения возникают каса­тельные напряжения, максимальные значения которых определятся по формуле:

кН/м² = 27,07 МПа,

где W_K = c³ = 0,4930,03³ = 13,310^-6 м³  геометрическая величи­на, играющая роль момента сопротивления при кручении стержней прямоугольного сечения. Здесь   коэффициент, зависящий от от­ношения большей стороны прямоугольника к меньшей (в данном случае при b/c = 2,  = 0,493).

4. Проверка прочности при расчетным сопротивле­нии R = 180 МПа. Расчетное напряжение по третьей теории прочности для плоского напряженного состояния определяется по формуле:

.

Участок АВ. Линейное напряженное состояние является част­ным случаем плоского ( = 0), поэтому в нашем случае:

, где R = 180 МПа.

Участок ВС. Проверка прочности по третьей теории:

36,25 МПа < 180 МПа.

Участок СD. Сначала найдем максимальное нормальное напря­жение от внутренних силовых факторов N, M_x  и M_y :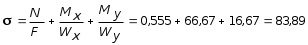

МПа.

Касательные напряжения в угловой точке от кручения равны 0. Имеет место линейное напряженное состояние:

МПа < 180 МПа.

Далее рассмотрим напряженное состояние в окрестности точки, где действует максимальное касательное напряжение  = 27,7 МПа. Имеет место плоское напряженное состояние: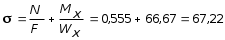

МПа;

МПа < 180 МПа.

Следовательно, так как условие обеспечения прочности во всех опасных точках участков ломанного бруса выполняются, то проч­ность конструкции в целом следует считать обеспеченной.