лекция изгиб. Плоский прямой изгиб

• Название: Плоский прямой изгиб
• Анкор: лекция изгиб
• Дата: 23.03.2023
• Размер: 1.44 Mb.
• Имя файла: лекция изгиб.doc
• Тип: Документы; #1010264
• страница: 4 из 5

Теории прочности

Как показывают экспериментальные исследования, прочность материалов существенно зависит от вида напряженного состояния. В общем случае нагруженного тела напряженное состояние в ка­койлибо точке вполне может быть определено величиной напря­жений в трех координатных плоскостях, проходящих через эту точку. При произвольном выборе положения координатных плос­костей, в каждой из них, вообще говоря, имеются и нормальные, и касательные напряжения. Для них вводятся соответствующие обо­значения в плоскости xy: _zz , _zx , _zy ; в плоскости xz: _yy , _yx , _yz; в плоскости yz: _xx , _xy , _xz . Здесь первый индекс показывает ориентацию площадки, в которой действует напряжение, т.е. какой из координатных осей она перпендикулярна. Второй индекс ука­зывает направление напряжения по координатной оси.

В каждой точке тела существуют три взаимно перпендикуляр­ные плоскости, свободные от касательных напряжений, носящие название главных площадок. Нормальные напряжения в этих пло­щадках называются главными напряжениями и обозначаются ₁, ₂, ₃. При этом всегда ₁ > ₂ > ₃. Заметим, что более подробно вопросы теории напряженного состояния в точке обсуждены в десятом разделе настоящей книги, и по данному вопросу имеется обширная литература.

Напряженные состояния разделяются на три группы. Напря­женное состояние называется: а) объемным или трехосным, если все главные напряжения ₁, ₂, ₃ не равны нулю; б) плос­ким или двухосным, если одно из трех главных напряжений равно нулю; в) одномерным или одноосным, если два из трех главных напряжений равны нулю.

Основной задачей теории прочности является установление критерия прочности, позволяющего сравнить между собой опас­ность различных напряженных состояний материала.

Выбранный критерий прочности должен быть обоснован на основе экспериментальных данных путем проведения испытаний различных материалов в зависимости от вида напряженного сос­тояния, как функция от соотношений между значениями главных напряжений.

Заметим, что, так как в настоящее время строгой единой тео­рии прочности материалов, в зависимости от вида напряженного состояния, не существует, поэтому при выполнении практических расчетов применяются упрощенные критерии.

Как отмечалось в п. 2.8, наиболее распространенным и наглядным критерием проверки конструкций на прочность, при простейших случаях напряженного состояния (сжатиерастяжение, кручение, чистый изгиб), является выполнение условия:

_max  , (5.38)

где _max  максимальное расчетное значение напряжения, возника­ющее в наиболее опасной точке конструкции;   допускаемое значение напряжения для материала конструкции.

В настоящее время при выполнении расчетов конструкций на прочность, при произвольных напряженных состояниях, широко используются три теории прочности.

Согласно первой теории критерием прочности является ограничение главного максимального напряжения:

_max = ₁  , (5.39)

где   предельное напряжение, полученное из опытов на одно­осное растяжение.

Основным недостатком этой теории является не учет двух других главных напряжений.

В основу второй теории прочности заложена гипотеза о том, что критерием оценки работы конструкции является ограни­чение наибольшего удлинения. В формулировке данного положе­ния через главные напряжения (₁ и ₂ ) это условие для плоского на­пряженного состояния записывается следующим образом:

₁   ₂   ,

где   напряжение, при котором было вызвано предельное уд­линение образца в опытах на одноосное растяжение;   коэф­фициент бокового расширения.

При объемном напряженном состоянии вторая теория проч­ности записывается в виде:

₁   (₂ ₃)   , (5.40)

Экспериментальная проверка не всегда подтверждает правиль­ность теории прочности наибольших линейных деформаций при простых нагружениях, т.е. при чистом растяжении или чистом сдвиге. Однако до настоящего времени эта теория имела широкое применение при выполнении инженерных расчетов..

В основу третьей теории прочности заложена гипотеза о том, что причиной разрушения материалов являются сдвиговые деформации, происходящие на площадках максимальных касатель­ных напряжений, т.е.

_max < , (5.41)

где _max  расчетное максимальное касательное напряжение, возни­кающее в опасной точке нагруженного тела;   предельное зна­чение касательного напряжения, полученное из опытов.

Для плоского напряженного состояния по третьей теории усло­вие прочности записывается в виде:

₁  ₂ <  . (5.42)

В случае поперечного изгиба балки (₂ = 0), если выразить главные напряжения ₁ и ₃ через  и , то условие прочности (5.42) преобразуется в виде:

, (5.43)

где R  расчетное сопротивление материала балки при изгибе.

 Пример расчета (задача № 10)

Дан пространственный консольный брус с ломаным очертани­ем осевой линии, нагруженный сосредоточенной силой Р = 1 кН и равномерно распределенной нагрузкой q = 2 кН/м. На рис. 5.34, а этот брус показан в аксонометрии в соответствии с прямоугольной системой координат xyz . Вертикальный элемент бруса имеет попе­речное сечение в виде круга диаметром d = 0,06 м (рис. 5.34, в), горизонтальные элементы бруса имеют поперечные сечения в виде прямоугольника (рис. 5.34, б). Ширина сечения b = d = 0,06 м, а высота сечения c = 0,5 d = 0,03 м. Ориентация главных осей попе­речных сечений на каждом участке показана на рис. 5.34, г.

Требуется:

1. Построить в аксонометрии эпюры M_x , M_y , M_z , N_z, Q_x , Q_y ;

2. Указать вид сопротивления для каждого участка бруса;

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N_z, M_x , M_y и M_z  (касатель­ными напряжениями от Q_x  и Q_y  можно пренебречь);

4. Проверить прочность при расчетном сопротивлении R = = 180 МПа.

Решение

1. 
   Построить в аксонометрии эпюры M_x , M_y , M_z , N_z, Q_x , Q_y . Заметим, что так как заданная система пространственная, при произвольном характере нагружения, в опорном сечении, где установлена заделка, возникает шесть опорных реакций (три опор­ные силы и три момента). Для определения опорных реакций, в данном случае, можем применить шесть уравнений равновесия ста­тики. Так как число независимых уравнений равновесия равно чис­лу опорных реакций, то можно сделать вывод, что рассматриваемая система в виде ломаного бруса, с заделанным одним концом, явля­ется статически определимой. Поэтому рассматриваемая система разрешима по методу сечений. Далее, учитывая особенности конст­рукции, определение величин внутренних усилий можно осущест­вить без предварительного вычисления величин опорных реакций.
   

Брус имеет три участка АВ, ВС и СD (рис. 5.34, г). При этом, после рассечения бруса на две части будем рассматривать равно­весие оставшейся части, не связанной с заделкой (чтобы избежать предварительного определения опорных реакций в заделке бруса). Внутренние силовые факторы можно рассматривать как реакции, действующие в сечении на оставшуюся часть со стороны отбро­шенной части, поэтому процесс определения шести величин M_x , M_y , M_z , N_z, Q_x , Q_y  может быть сведен к известному процессу оп­ределения опорных реакций.

Следует отметить, что при определении опорных реакций их направление можно указать произвольно, а затем из решения урав­нения равновесия будет ясно, как в действительности действует ре­акция: если результат положительный, то реакция действует имен­но так, как мы предварительно указали, если отрицательный  то наоборот.

При построении эпюр будем руководствоваться следующими правилами:

 нормальная сила N_z считается положительной, если она вызы­вает растяжение бруса;

 крутящий момент M_z  считается положительным, если при взгляде на сечение со стороны внешней нормали он виден враща­ющим брус по ходу часовой стрелки;

 поперечная сила Q_x считается положительной, если при взгляде со стороны положительного направления оси y она стре­мится вращать оставшуюся часть бруса по ходу часовой стрелки от­носительно ближайшей точки на оси бруса (для поперечной силы Q_y  то же, по отношению к x);

 ординаты эпюр Q_x и Q_y следует откладывать перпендикуляр­но оси бруса в плоскости действия этих сил и указывать знак;

 ординаты эпюр М_x и М_y будем откладывать перпендикулярно оси бруса со стороны растянутого волокна.





Участок АВ (0 z₁a).

Оставшаяся часть изображена на рис. 5.34, д. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­дината z₁ увеличивается от точки А к точке В. Для определения N покажем ее в направлении от сечения, т.е. растягивающей, и соста­вим уравнения равновесия: z = 0;    N_z = 0. Из М_x = 0 следует М_x = 0 (рис. 5.35, а).

Для определения М_z покажем его так, чтобы при взгляде на сечение он был виден вращающим брус по часовой стрелке, и составим уравнения равновесия (рис. 5.35,б):

m_z = 0; М_z = 0.

Для определения Q_x и Q_y покажем их положительными в соот­ветствии с выбранным правилом знаков и составим уравнения рав­новесия:

x = 0, Q_x  P = 0, Q_x = P = 1 кН;

y = 0, Q_y = 0.

Эпюра Q_x представляет собой прямоугольник (рис. 5.35, в) с ординатой, равной 1, лежащей в плоскости действия этого силово­го фактора. Составляем уравнение равновесия:

M_y = 0, М_y + Рz = 0, М_y = Pz.

Ординаты эпюры M_y линейно зависят от z:

z = 0,  M_y = 0;      z = a,  M_y = Pa = 10,3 = 0,3 кНм.

Знак минус указывает на то, что в действительности изгибаю­щий момент M_y вызывает растягивающее напряжение в правой части поперечного сечения, поэтому ординаты эпюры M_y отклады­ваются в правую сторону.

Участок ВC (0 z₂b).

Оставшаяся часть изображена на рис. 5.34, e. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­дината z₂ увеличивается от точки В к точке С. Процесс опреде­ления внутренних силовых факторов на этом участке такой же, как и на предыдущем. Важно отметить, что на оставшейся части соот­ветствующий внутренний силовой фактор удобно показывать непо­средственно перед его определением  для того, чтобы не затем­нить чертеж. При этом N_z, M_z , Q_x , Q_y  показывают в положи­тельном направлении в соответствии с принятым правилом знаков, а изгибающие моменты M_x и M_y  наугад из двух возможных направлений (рис. 5.34, e):

z = 0,  N_z = 0;     M_z = 0,  M_z + Pa = 0,  M_z = Pa = 0,3 кНм.

Плоскость прямоугольной эпюры произвольна (рис. 5.35, б).

x = 0,   Q_x   P = 0, Q_x  = P = 1 кН.

Эпюра Q_x в виде прямоугольника показана на рис. 5.35, в.

y = 0, Q_y   q z = 0; Q_y  = q z ;

z = 0,    Q_y  = 0; z = 0,6 м,    Q_y  = 20,6 = 1,2 кН.

Эпюра Q_y в виде треугольника показана на рис. 5.35 е.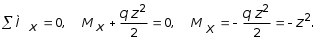



Ординаты M_x изменяются по закону квадратной параболы.

z = 0,    M_x = 0; z = 0,6 м,    M_x = 0,36 кНм;

= 2 z = 0; z = 0 точка экстремума в эпюре M_x в сечении z = 0.

Знак минус указывает, что растягивающие напряжения возни­кают не в ближней части сечения, а в дальней. При этом наблюда­тель ориентирован относительно глобальной системы координат xy, показанной на рис. 5.34, а следующим образом: ось x направле­на к наблюдателю, поэтому ординаты M_x





Рис. 5.35

откладываем в дальнюю сторону (рис. 5.35, а).

M_y = 0,    M_y + P z = 0,    M_y = P z;

z = 0,    M_y = 0; z = 0,6 м,    M_y = 0,6 кНм.

Эпюра M_y  треугольная. Растягивающие напряжения возника­ют в правой части сечения  ординаты откладываем вправо.

Участок CD (0 z₃c₁).

Оставшаяся часть изображена на рис. 5.34, ж. В центре сечения помещаем систему координат. Оси x и y совпадают с направлением главных осей инерции сечения, показанных на рис. 5.34, г. Коор­динаты z₃ увеличиваются от точки С к точке D. Повторяя все рас­суждения, проведенные на предыдущих участках, будем иметь следующее (рис. 5.34, д):

z = 0,    N  P = 0,    N = P = 1 кН;

M_z = 0, 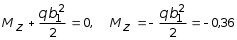    кНм.

Эпюра M_z  в виде прямоугольника. Плоскость изображения произвольная:

x = 0,    Q_x + q b₁ = 0,    Q_x = q b₁ = 20,6=1,2 кН.

Эпюра Q_x  в виде прямоугольника в плоскости действия Q_x.

y = 0,    Q_y = 0;M_x = 0, M_x + P b₁ = 0, M_x = P b₁ = 0,6 кНм.

Эпюра M_x  в виде прямоугольника. Растягивающие напряже­ния при изгибе возникают в нижней части поперечного сечения ординаты эпюры откладываем вниз.

