кп. 1 часть. Виды нагружения. Напряжение, основные понятия. Реальный объект
 Скачать 2.61 Mb.
|
|
Уравновесим отсеченную часть. Так как отсеченная часть тела находится в равновесии, то для определения шести неизвестных составим шесть уравнений равновесия:   - нормальная сила равна сумме проекций всех внешних сил,действующих на отсеченную часть, на продольную ось z;  - поперечные силы равны по величине суммам проекций всех внешних сил, действующих на отсеченную часть, на оси x и y соответственно;  - крутящий момент равен сумме внешних моментов, действующих на отсеченную часть, относительно оси z; ;  - изгибающие моменты равны суммам внешних моментов, действующих на отсеченную часть, относительно осей х и у соответственно.29. Понятие о напряжениях, деформациях и перемещениях. Нормальные и касательные напряжения. Вектор полного перемещения. Линейная и угловая деформация Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции. Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R (рис. I.1.10а). Величина отношения R/A=pсрназывается средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю: 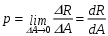 Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения. Очевидно, что  . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (tzх, tzу). Размерность напряжений – Н/м2 (Па).При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела. Отнесем недеформированное тело к декартовой системе координат Oxyz. Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М/ , характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'—r называется вектором, перемещений точки М. 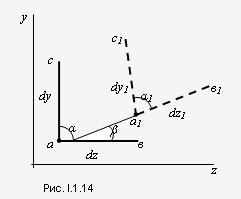 Под действием внешних сил любое тело деформируется, т.е. его форма и размеры изменяются, а точки тела меняют положение в пространстве. Пусть имеется тело с приложенными к нему силами Рi. Мысленно через точку а в направлениях осей у и z проведем бесконечномалые отрезки ав иас, длины которых dy и dz. После деформации бруса отрезки примут положение, изображенное штриховой линией (рис. I.1.14). Точка а переместится в положение а1. Величина аа1, равная изменению координат точки называется линейным перемещением точки а. Отрезки ав и ас займут новые положения а1в1 и а1с1. Их длины изменяются на Δdy и Δdz и называются абсолютными линейными деформациями. Угол между начальным положением отрезка ав и конечным - а1в1 - называются угловым перемещением b. Линейные перемещения измеряются в единицах длины, угловые - в радианах или градусах. Отношение приращения длины отрезка к его начальной длине представляет собой относительную линейную деформацию, т.е.  . Аналогично  .Линейные деформации величины безразмерные. Изменение первоначально угла между отрезками ав и ас после приложения к телу нагрузки, выраженное в радианах, представляет собой угловую деформацию  .Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке. 30. Растяжение и сжатие. Определение внутренних сил. Натяжение в попересных и наклонных сечениях. Под растяжением понимается такой вид нагружения, при котором в поперечном сечении стержня возникают только нормальные силы, а все прочие внутренние силовые факторы равны 0. Сжатие отличается от растяжения только знаком силы N. При растяжении нормальная сила N направлена от сечения, а при сжатии - к сечению. Таким образом при анализе внутренних сил сохраняется единство подхода к вопросам растяжения и сжатия. 31) Продольная и поперечная деформация при растяжении и сжатии. Коэффициент Пуассона. Закон Гука при растяжении. Потенциальная энергия деформации. Продольная деформация:   - относительная продольная деформация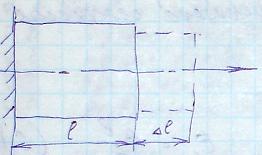.Мы имеем линейное одноосное напряжённое состояние. Это относительная продольная деформация. 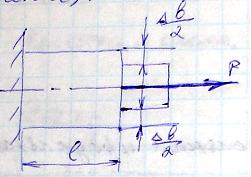 Поперечная деформация: При растяжении тела происходит изменение его поперечного сечения (сужение).  Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной:  - коэффициент Пуассона. Характеризует свойства материала. Определяют его экспериментальным путём. Для всех металлов числовые значения этого коэффициента лежат в пределах 0,25…0,35.Закон Гука. Он установил связь между напряжением, растяжением и продольной деформацией.  где Е – коэффициент пропорциональности (модуль упругости материала).Модуль упругости характеризует жёсткость материала, т.е. способность сопротивляться деформациям. Потенциальная энергия деформации: Внешние силы, приложенные к упругому телу, совершают работу. Обозначим её через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идёт на сообщение скорости массе тела, т.е. преобразуется в кинетическую энергию К. Баланс энергии имеет вид А = U + К. 32. Экспериментальное изучение свойств материалов при растяжении и сжатии. Диаграмма растяжения. Основные характеристики материалов (механические). По диаграмме растяжения оцениваются механические характеристики материала. Д  еформация рассматривается для упругопластичного материала (малоуглеродистая сталь).т. А – предел пропорциональности  ;т. В – предел упругости  ;т. С – предел текучести  ;т. D – временный предел прочности; т. Е – разрушение образца. - это такое максимальное напряжение, до которого материал следует закону Гука. - такое максимальное напряжение, при котором после снятия нагрузки материал вернётся в исходное состояние. - это такое напряжение, при котором без видимого изменения нагрузки материал течёт. Если снимем нагрузку, материал вернётся в положение  .СD – зона упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более медленным (в сотни раз), чем на упругом участке. т. D соответствует максимальному напряжению, при котором материал не разрушается. т. E – соответствует разрушению образца. tg  - даёт модуль упругости.Этот метод измерения характеристик материала самый простой, широкоиспользуемый и доступный. К основным механическим характеристикам материала относят пластичность, хрупкость и твёрдость. Способность материала без разрушения получать большие остаточные деформации носит название пластичности. Свойство пластичности имеет решающее значение для таких технологических операций, как штамповка, вытяжка, волочение, гибка и др. Мерой пластичности является удлинение  при разрыве. Чем больше , тем более пластичным считается материал.Свойством, противоположным пластичности, является хрупкость, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материалы, обладающие этим свойством, называются хрупкими. Диаграмма растяжения хрупких материалов не имеет площади текучести и зоны упрочнения. П  од твёрдостью понимается способность материала противодействовать механическому проникновению в него посторонних тел.Наиболее широкое распространение получили методы измерения твёрдости по Бринеллю и по Роквеллу. а  ) Твёрдость по Бринеллю [НВ] – в поверхность исследуемой детали вдавливают стальной шарик диаметром 10 мм.б) Твёрдость по Роквеллу [HRC]– алмазный острый наконечник. В результате испытаний на твёрдость удаётся определить прочностные показатели материала, не разрушая деталь.  33. Расчёт на прочность при растяжении и сжатии. Допускаемое напряжение и коэффициент запаса. При проектировании элемента конструкции необходимо определить размеры, обеспечивающие его безопасную работу при заданных нагрузках. Для успешного решения этой задачи необходимо исходить из того, чтобы наибольшее расчётное напряжение в поперечном сечении элемента конструкции, возникшее при заданной нагрузке, было меньше того предельного напряжения, при котором возникает опасность появления пластической деформации или опасность разрушения. Отношение предельного напряжения  к расчётному  называется коэффициентом запаса прочности s: .При расчёте элемента конструкции коэффициент запаса прочности задаётся заранее и называется нормативным или требуемым и обозначается [s]. Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого т.е. s>=[s] Это неравенство выражает условие прочности элемента конструкции. Разделив предельное напряжение на нормальный коэффициент запаса, получим допускаемое напряжение  : Тогда условие прочности можно выразить неравенством  т.е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нём, не превышает допускаемого. 34. Чистый сдвиг. Напряжение и деформация при сдвиге. Чистым сдвигом называется такой вид нагружения, когда на гранях параллелепипеда действует только касательное напряжение. П  од действием сил происходит деформация.Происходит перемещение материала на величину . - угол сдвига; - перемещение;h – расстояние действия сил. Из     - назначается коэффициент запаса > 1. 35. Кручение бруса круглого, поперечного сечения. Напряжение и деформация при кручении. Определение максимальных касательных напряжений. Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и поперечные силы) равны нулю. Расчётная схема закрученного образца:   - полный угол закручивания.Берём элементарный участок:   - относительный угол поворота, приходящийся на единицу длины.  зависит от радиуса поперечного сечения круглого стержня.Внутренняя сила в точке К определяется    - полярный момент инерции поперечного сечения – геометрическая характеристика, зависящая от размеров поперечного сечения.  - зависимость при кручении. 36. Геометрические характеристики брусьев круглого, поперечного сечения при кручении. Потенциальная энергия деформации при кручении. 11) Расчёт валов на прочность и жёсткость при кручении. Условие прочности при кручении  где  - полярный момент сопротивления при кручении.  - допускаемое касательное напряжение. n – коэффициент запаса. Для проектируемого вала: Из условий прочности на кручение определяем минимальный диаметр вала:  , ммгде  = 10…20 МПа.Берётся заниженное значение допускаемого напряжения т.к. определяется минимальный диаметр вала. Расчёт на жесткость: Упругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колёс и т.п. От прогиба вала в зубчатом зацеплении возникает концентрация нагрузки по длине зуба. Перемещение при кручении валов постоянного диаметра определяют по формуле  где - угол закручивания вала, рад; T – крутящий момент; G - модуль упругости при сдвиге;l – длина закручиваемого участка вала;  - полярный момент инерции сечения вала.Если вал ступенчатый и нагружен несколькими T, то угол определяют по участкам и затем суммируют.37. Моменты инерции сечения. Вычисление моментов инерции брусьев прямоугольного и круглого сечения.  Представим, что сечение разделено на множество элементарных площадок dA (см. рис. – изображена одна из них), координаты которых x и y. Тогда интегралы  и  Называются моментами инерции сечения относительно осей x и y, а интеграл  принято называть центробежным моментом инерции сечения относительно осей x и y.Величина площади dA положительна, поэтому независимо от знака координаты x или y осевые моменты инерции всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным в зависимости от расположения сечения относительно осей x или y. Зависимость между осевыми и полярными моментами инерции  Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Моменты инерции относительно осей, проходящих через центр тяжести сечения, называются центральными. 38.Прямоугольное сечение. П  рямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.Главный центральный момент инерции относительно оси x  Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим  Окончательно  Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:  39.Круглое сечение Д  ля круга главные центральные моменты инерции относительно осей x и y равны между собой.Поэтому из равенства , получаем или  ,где  .Подставим значение Jp и получим для круглого сечения  40. Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры. Дифференциальные зависимости при изгибе. Под изгибом понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты. В  се элементы конструкции подвергаются изгибу. Все элементы конструкции рассчитывают на изгиб, при этом принимают расчётную схему конструкции.Балка – это брус, который воспринимает поперечные нагрузки и работает на изгиб. Это наиболее распространённая схема для множества конструкций в технике – балка на 2х опорах. Виды изгиба: чистый; - поперечный; - прямой; - косой.  Чистый изгиб – вид нагружения, когда в поперечном сечении балки действует только изгибающий момент. Поперечный изгиб – когда на поперечное сечение действует одновременно изгибающий момент и поперечная сила (общий случай). Пример чистого изгиба:   - удельная нагрузка, приходящаяся на единицу длины конструкции.Правило знаков поперечных сил при изгибе:  Правило знаков изгибающих моментов:  Правило проверки правильности построения эпюр нагружения: В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки. Этапы: 1 Выбор расчётной схемы; 2 Анализ системы сил (система сил доводится до равновесного состояния); 3 Определение опорных реакций (ур-е статики) из условия равновесия; 4 Определение поперечных внутренних сил на каждом участке конструкции пользуясь методом сечения. 41. Примеры элементов конструкций, работающих на изгиб. Типы опор и определение опорных реакций. Конструкции опор: а) Шарнирно – неподвижная опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).   б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки.   в) Консольная опора – жёстко замоналиченая консоль.  Реакции в опорах определяют из условия равновесия (уравнение статики).  42. Расчет на прочность при изгибе Под изгибом понимается такой вид нагружения , при котором в поперечных сечениях бруса возникают изгибающие моменты. Большей частью , в поперечных сечениях бруса наряду с изгибающими моментами возникают так же и поперечные силы, в этом случае изгиб называется поперечным. При изгибе балки происходит искривление ее оси в плоскости действия внешней силы. |