кп. 1 часть. Виды нагружения. Напряжение, основные понятия. Реальный объект
 Скачать 2.61 Mb. Скачать 2.61 Mb.
|
|
r 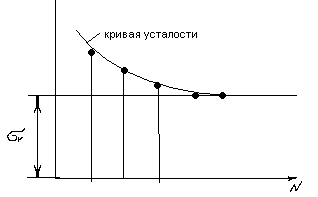  53.Влияние концентраций напряжений, состояния поверхности и размеров детали на усталостную прочность Концентраторы напряжений связаны с конструкторской формой детали. Источник появления микротрещин. Состояние поверхности: а) шлифование KF б) токарная обработка в) часовая токарная обработка Масштаб 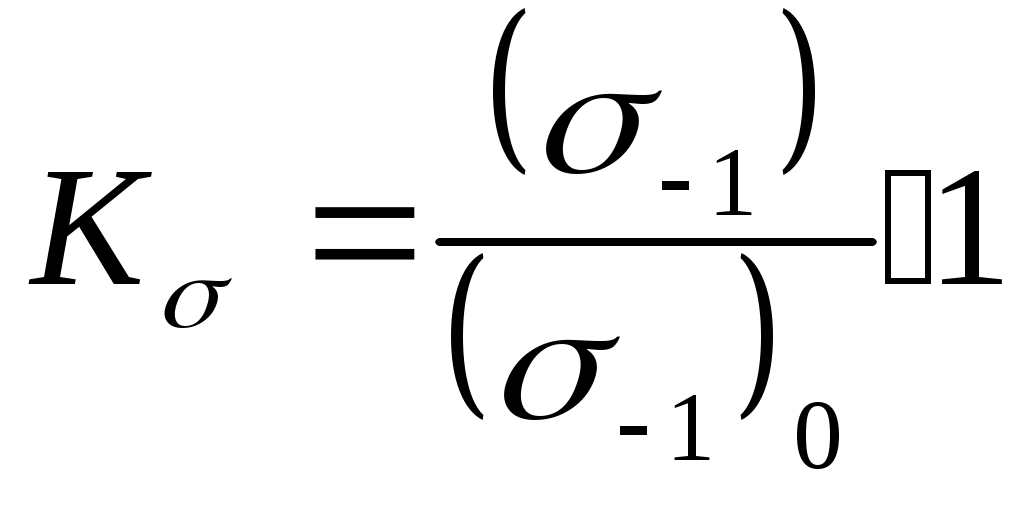 2) 2)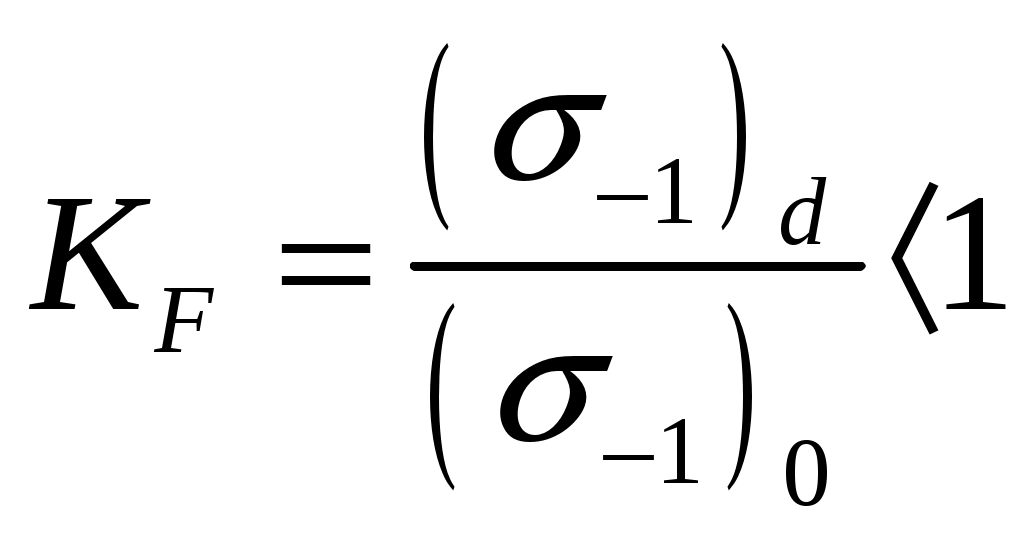 - коэф-т состояния 3)лабаритный фактор - коэф-т состояния 3)лабаритный фактор 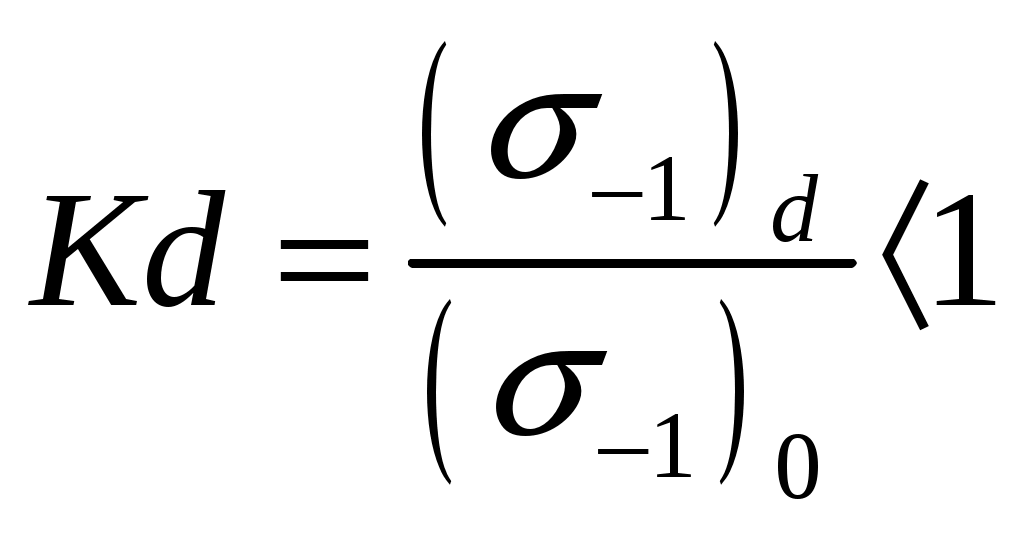 ; ; 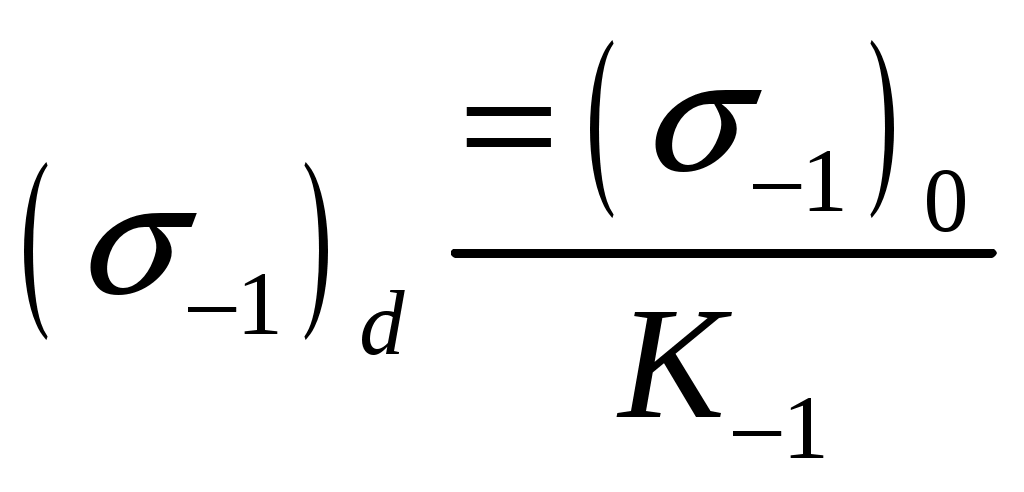 ; ; 54. Расчет на прочность при переменных напряжениях. 1.Расчет конструкции, находящейся под действием переменных напряжений начинается со стат расчета конструкции, целью которого является определение размеров конструкции при заданной нагрузке. 2. Конструирование конструкции -уточнение формы конструкции, только после этого проводится уточненный проверочный расчет на усталость, в результате которого определяют коэффициент запаса прочности. Определение запаса при изгибе: При кручении: Для сложного напряженного состояния определяется коэф-т запаса усталости: 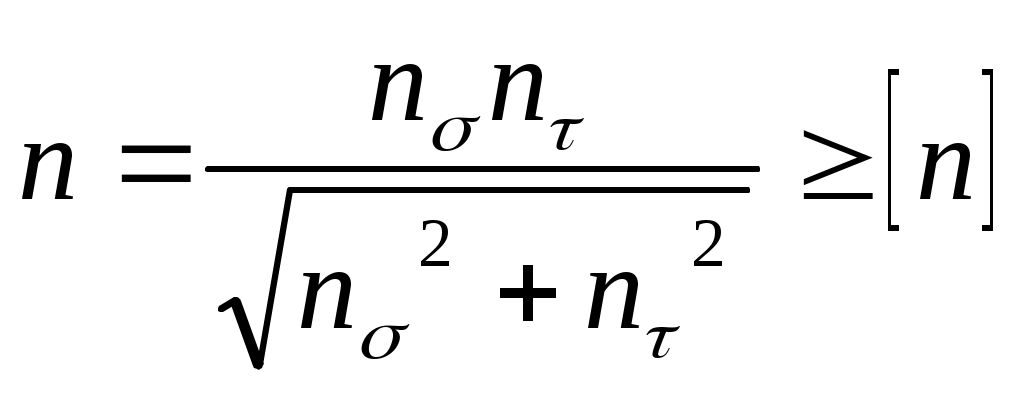 Общий случай – случай несимметричного цикла нагружения. Коэффициенты запаса определяют по изгибу. 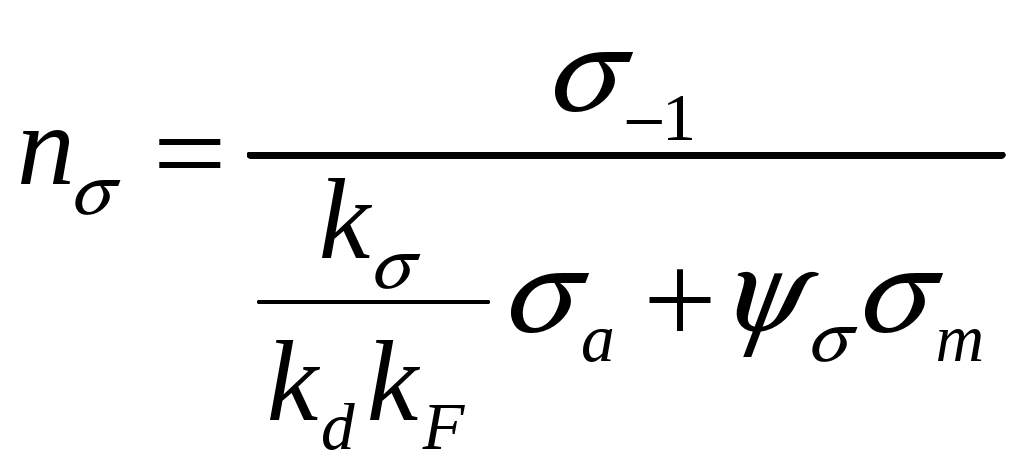 , ,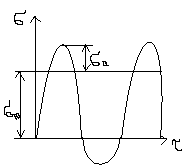 Для кручения: 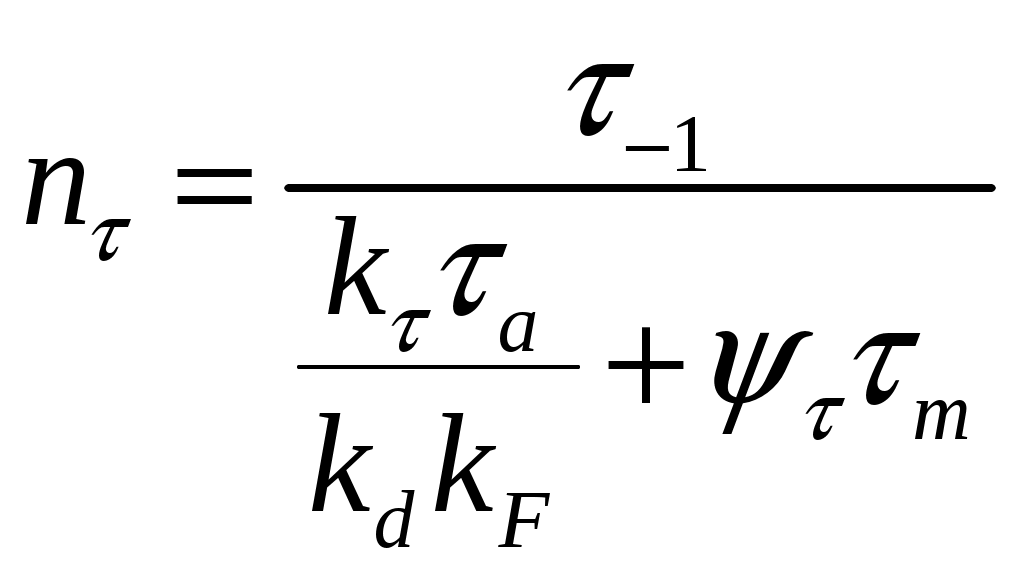 , , При несимметричном цикле нагружения После расчета на усталость проводится статический расчет на сопротивление пластичным деформациям 55. Местные напряжения. Концентрация напряжения 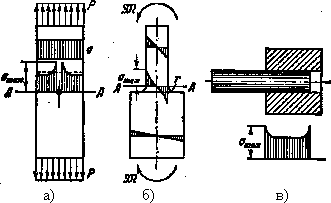 Многочисленные теоретические и экспериментальные исследования показывают, что в области резких изменений в форме упругого тела (входящие углы, отверстия, выточки), а также в зоне контакта деталей возникают повышенные напряжения с ограниченной зоной распространения, так называемые местные напряжения. Например, при растяжении полосы с небольшим отверстием рис. 1, а) закон равномерного распределения напряжений вблизи отверстия нарушается. Напряженное состояние становится двухосным, а у края отверстия появляется пик напряжения. Аналогично при изгибе ступенчатого стержня (рис. 1, б) в зоне входящего угла возникает повышенное напряжение, величина которого зависит в первую очередь от радиуса закругления r. При прессовой посадке втулки на вал (рис. 1, в) у концов втулки и вала также возникают местные напряжения. Подобных примеров можно привести очень много. Основным показателем местных напряжений является теоретический коэффициент концентрации напряжений: где В 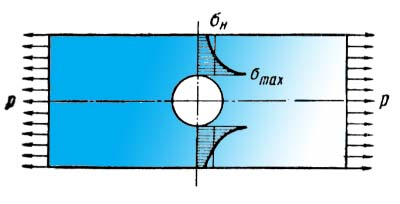 озле отверстий, выточек и других мест резкого изменения конфигурации детали возникает концентрация напряжений (рис. 14, 15). озле отверстий, выточек и других мест резкого изменения конфигурации детали возникает концентрация напряжений (рис. 14, 15). Рис.14. Концентрация напряжений у отверстия 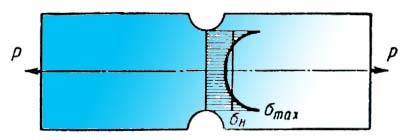 Рис.15. Концентрация напряжений у выточки Отношение наибольшего напряжения в зоне концентрации к номинальному называется коэффициентом концентрации: Номинальные напряжения рассчитываются по формулам сопротивления материалов. Чем резче меняется форма тела, тем больше коэффициент концентрации напряжений. Большие местные напряжения возникают также в зонах приложения сосредоточенных сил. Такие напряжения называются контактными. 56. Контактные напряжения. Формула Герца Определение напряжений, возникающих в местах соприкосновения тел (контактных напряжений), является задачей теории упругости, и в курсе сопротивления материалов удается либо дать без вывода формулы для определения формы и размеров площадки контакта и напряжений в окрестности этой площадки, либо вывести простейшие формулы теории контактных напряжений, например формулы, определяющие площадку контакта, сближение центров шаров и напряжения в окрестности контакта двух шаров. Однако эта задача очень важна, особенно для машиностроения, и, вероятно, ничего не говорить о контактных напряжениях в курсе сопротивления материалов невозможно. Начало теории контактных напряжений было заложено в работе Г.Герца [378], опубликованной в 1895 г. Им рассмотрены две задачи: первоначальное точечное касание деталей, например, касание двух шаров или шара и кольца в шарикоподшипнике и первоначальное касание по линии, например, касание двух цилиндров или ролика и кольца в роликоподшипнике. При этом предполагается, что материал деталей однородный, изотропный и упругий. Для определения удельного давления между деталями с цилиндрическими поверхностями существует формула Герца, которая для пары вогнутой и выпуклой цилиндрических поверхностей имеет вид Pmax * E 1 1 C max = 0.418 * -----------*(--- - ---) 4.4.2 B R1 R2 где: R1 - радиус шейки, R2 - радиус втулки, R=R2-R1 - радиальный зазор, E - приведенный модуль упругости 1 1 1 ------ = ------ + -------- 4.4.3 E E1 E2 E1 - модуль упругости материала шейки, E2 - модуль упругости материала втулки, Поскольку R< 1 1 R (--- - ---) = -------- R1 R2 R1**2 таким образом удельные контактные давления будут: Pmax * E * R C max = 0.418 * -------------- 4.4.4 B * R1 Эта формула дает способы, с помощью которых можно снизить контактное давление. Соотношение удельного давления полученного по формуле 4.4.1 , полученного по формуле Герца 4.4.4 определяется так: K max 1 P max ------- = -------- * ------------ 4.4.5 C max 2* 0.418 E* B* R Если сопоставить эти величины для конкретных значений использованных в примерах, то получим С max/ Р max= 2.37, откуда видно, что контактные напряжения по Герцу больше максимальных значений, получаемых традиционным расчетом. 57.Устойчивость. Форма равновесия в деформированном состоянии считается устойчивой, если система после снятия нагрузки примет первоначальное состояние |
