Выполнение работ по построению и уравниванию геодезических сетей сгущения, съемочных сетей, спутниковых навигационных систем в Волгоградской области, г. Волгоград
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
2.3. ВЫЧИСЛЕНИЕ ПОПРАВОК ЗА ЦЕНТРИРОВКУ И РЕДУКЦИЮДля приведения направлений к центрам пунктов вычисляем поправки в направления за центрировку и редукцию, используя значения угловых и линейных элементов приведения. Выражения для определения этих поправок получаем из следующих выражений. Поправки за «центрировку» «с»-центрировка 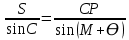 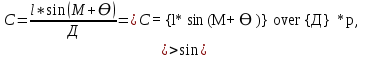 где Ɩ – линейный элемент центрировки, ϴ – угловой элемент центрировки, Д – расстояние от исходного пункта до теодолита р =206265" Если sin(M+ ϴ)<180°, то «С» положительная. Если sin(M+ ϴ)>180°, то «С» отрицательная. Поправки вычисленные по элементам центрировки данного пункта вводимв направления, измеренные с этого пункта на все наблюдаемые пункты, включая начальное направление Поправки за «редукцию» «r»-редукция При наблюдении с пункта на пункт, визирование производим на визирный цилиндр, проекция которого не совпадает с центром пункта. 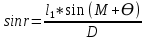 r"=  2.4. ПРИВЕДЕНИЕ ИЗМЕРЕННЫХ НАПРАВЛЕНИЙ К ЦЕНТРАМ ПУНКТОВ И ОЦЕНКА КАЧЕСТВА УГЛОВЫХ ИЗМЕРЕНИЙВ каждое измеренное направление вводим суммарную поправку за центрировку и редукцию. После введения преобразованных поправок получаем направления, приведенные к центрам пунктов. При вычислении суммарных поправок (с+r), следует помнить, что поправки за центрировку «с», берут из вычислений на исходном пункте (на котором произведены наблюдения), а поправки за редукцию «r» – из вычислений на том пункте, на который выполнялись наблюдения. Приведенные направления выписываем на схему сети и вычисляем углы в треугольниках как разности соответствующих приведенных направлений. Полученные данные используем в дальнейшем при уравнивании сети. В каждом треугольнике подсчитываем сумму углов 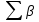 и угловую невязку: и угловую невязку: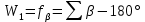 = -0°00’14’’ = -0°00’14’’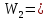 -0°00’01’’ -0°00’01’’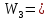 -0°00’08’’ -0°00’08’’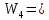 -0°00’01’’ -0°00’01’’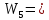 +0°00’09’’ +0°00’09’’Для триангуляции 2-го разряда допустимая угловая невязка в треугольнике W=41". По невязкам в треугольниках вычисляют среднюю квадратическую погрешность измерения угла по формуле Ферреро: 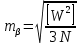 =3´´ =3´´где N – число треугольников в сети 2.5. УПРОЩЕННОЕ УРАВНИВАНИЕ УГЛОВ ЦЕПИ ТРЕУГОЛЬНИКОВ МЕЖДУ ДВУМЯ ИСХОДНЫМИ СТОРОНАМИВ данной сети возникает девять условных уравнений: пять условных уравнений фигур (треугольников), одно условие дирекционных углов, одно условное уравнение базисов и два условных уравнения координат. Так как рассматриваемая сеть несвободна, выделим три группы условных уравнений. В первую группу отнесем уравнения с коэффициентами при поправках ±1: пять условий фигур и одно условие дирекционных углов. Условное уравнение фигур: 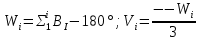 Вычисление вторичных поправок: Условное уравнение базиса: 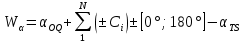 = -9’’ = -9’’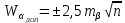 =36’’ =36’’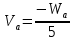 = -1,80’’ = -1,80’’Вычисление вторичных поправок: Условное уравнение базиса: 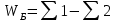 = -4’’ = -4’’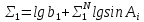 = 53,002933 = 53,002933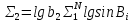 = 53,002937 = 53,002937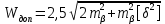 = ±34’’ = ±34’’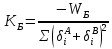 = +0,24 = +0,24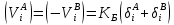 Контроль: 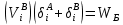 Условное уравнение координат: 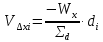 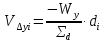 |
