Выполнение работ по построению и уравниванию геодезических сетей сгущения, съемочных сетей, спутниковых навигационных систем в Волгоградской области, г. Волгоград
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
4.4. ВЫПОЛНЕНИЕ ГРАФИЧЕСКОГО КОНТРОЛЯ РЕШЕНИЕ ЗАДАЧИ ТРИЛАТЕРАЦИИ ПО ЧЕРТЕЖУ МАСШТАБА 1:5000ЗАДАЧА: На ватман А3 нанести координаты исходных пунктов А, В, С и определяемого пункта Р в масштабе 1:5000, и полученную сеть трилатерации в виде линейной засечки сравнить с вычисленными элементами из оценки точности. ПОРЯДОК РЕШЕНИЯ: 1. На ватмане А3 наносим координаты исходных пунктов А,В,С и определяемого пункта Р в масштабе 1:5000. Выполняем графический контроль по вычисленным элементам hA, hB, hC, δ1,δ2,δ3, d1, d2, d3 путем сравнения их с элементами, снятыми графически с сети трилатерации. Таблица. Графический контроль
Схема сети трилатерации в виде линейной засечки на ватмане А3 в масштабе 1:5000 (Приложение 15) 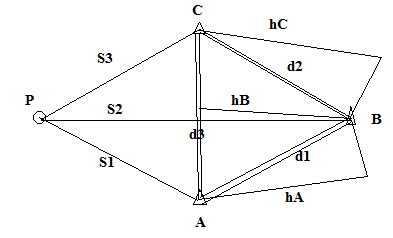 Рисунок 2. Пример схемы сети трелатерации в виде линейной засечки на ватмане А3 в масштабе 1:5000. 5. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА НИВЕЛИРНЫХ СЕТЕЙ IV КЛАССА 5.1. УРАВНИВАНИЕ СИСТЕМЫ НИВЕЛИРНЫХ ХОДОВ С ОДНОЙ УЗЛОВОЙ ТОЧКОЙ СПОСОБОМ СРЕДНЕГО ВЕСОВОГОЗАДАЧА: на местности проложены нивелирные ходы, проложенные между исходными реперами А, В и С с отметками НА, НВ и НС, сходятся в одной узловой точке О, образуя три одиночных хода. Измерены длины ходов Li, число станций в ходе ni и превышения по каждому ходу. Требуется уравнять нивелирный ход IV класса с одной узловой точкой. ПОРЯДОК РЕШЕНИЯ: 1. На схему (Рисунок 3) выписываем отметки исходных реперов, суммы измеренных превышений по ходам и длинны ходов по вариантам.  Рисунок 3. Схема нивелирования ходов с одной узловой точкой 2. Определяем допустимость невязок; расчеты выполняем по самым коротким ходам. Количество комбинаций принимаем на одну меньше числа ходов. Фактические и допустимые невязки по ходам рассчитываем, как fh = Σhпр. – (Нкон.-Ннач.), для нивелирования IV класса fhдоп. = ±20мм 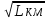 или fhдоп. = ±5мм или fhдоп. = ±5мм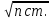 3. Находим частные значения отметки узловой точки по каждому ходу: Н1 = НА + Σh1 Н2 = НВ + Σh2 Н3 = НС + Σh3 4. Приняв веса суммы превышений по каждому ходу Рi = 1/Li, вычисляем вероятнейшее значение отметки узловой точки по формуле среднего весового: НО = 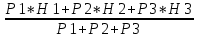 = = 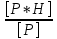 В результате систему нивелирных ходов с одной узловой точкой (рисунок 3) можно рассматривать как систему одиночных нивелирных ходов с высотой конечной точки равной НО. 5. Находим невязки в сумме превышений пол каждому ходу: W1 = HO – H1 W2 = HO – H2 W3 = HO – H3 6. Выполняем оценку точности результатов уравнивания: Вычисляем среднюю квадратическую погрешность в превышении нивелирного хода длиной 1 км, т. е. погрешность единицы веса mкм = 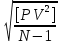 где mкм – средняя квадратическая погрешность превышения в ходе длиной 1 км; vi = - Wi – поправка в сумму превышений хода; N – число ходов (в нашей задачи N = 3). Находим среднюю квадратическую погрешность высоты узловой точки: МО = 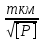 Все расчеты по уравниванию системы нивелирных ходов с одной узловой точкой свели в Таблицу «Уравнивание системы нивелирных ходов с одной узловой точкой» Таблица. Уравнивание системы нивелирных ходов с одной узловой точкой НА = 118,535 м НВ = 125,758 м НС = 111,200 м
fh1+2 = 8 ммfh1+3 = 0 мм fh2+3 = -8 мм fh1+2доп =±67мм fh1+3доп = ±77мм fh2+3доп =±66 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
