Выполнение работ по построению и уравниванию геодезических сетей сгущения, съемочных сетей, спутниковых навигационных систем в Волгоградской области, г. Волгоград
 Скачать 1.17 Mb.
|
5.4. УРАВНИВАНИЕ НИВЕЛИРНОЙ СЕТИ IV КЛАССА СПОСОБОМ ПОЛИГОНОВ ПРОФ. В. В ПОПОВАЗАДАЧА: Требуется уравнять несвободную нивелирную сеть IV класса, схема которой приведена на рисунке 6. Уравнивание выполнить по вариантам, приведенным в таблице 8. ПОРЯДОК РЕШЕНИЯ: Способ применяют для уравнивания, как свободных, так и несвободных сетей нивелирных ходов. Свободными называют такие геодезические сети, в которых имеются только необходимые исходные элементы: координаты одного исходного пункта и дирекционный угол исходного направления, высота одного исходного репера и т. п. Наличие в сети избыточных исходных данных вызывает дополнительные условия, которым должны удовлетворять уравненные величины; такие сети являются несвободными. Данный способ применяют для уравнивания как свободной, так несвободной сети полигонов. Он заключается в последовательном распределении невязок пропорционально длинам сторон (числу штативов) непосредственно на схеме, без составления уравнений поправок и ведомостей вычислений. На рисунке 6 представлена несвободная нивелирная сеть. Методика уравнивания несвободной сети сводиться к уравниванию свободной сети путем введения фиктивных звеньев, соединяющих исходные пункты. Число фиктивных звеньев должно быть на 1 меньше числа исходных пунктов. Длину фиктивных звеньев принимают равной 0, следовательно, в фиктивные звенья поправки не вводят. Уравнивание выполняют в следующей последовательности: 1. На схему сети выписываем все данные, необходимые для уравнивания: номера полигонов, длины звеньев между исходными и узловыми точками, стрелками указываем направления нивелирования, превышения по каждому звену, невязки в превышениях по каждому полигону, соответствующие по ходу полигона по ходу часовой стрелки, допустимые высотные невязки. 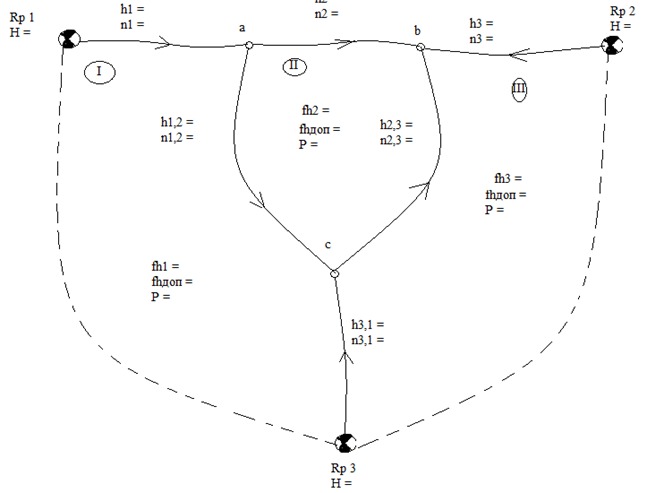 Рисунок 6. Схема несвободной нивелирной сети 2. Составляем схематический чертеж сети (Рисунок 7), на котором производим вычисление поправок на звенья. 3. В центре каждого полигона строим рамочки, внутри которых записываем невязки. Вне полигона у каждого его звена строим рамочки для записи поправок у внешних (смежных) звеньев сети будет по одной рамочке, а у внутренних (смежных) – по две. 4. Для всех звеньев вычисляем красные числа, как отношение длины звена ni к периметру полигона Рi: Ki = 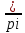 5. Полученные значения красных чисел записываем красным цветом над соответствующими рамочками, расположенными вне полигона около его звеньев. Для каждого полигона сумма красных чисел должна быть равна единице. 6. Приступаем к распределению невязок в полигонах пропорционально красным числам звеньев, начиная с полигона с наибольшей, по абсолютному значению невязкой. Поправка приходящееся на звено определяется как произведение невязки полигона на красное число звена. Полученные поправки по звеньям записываем в соответствующих рамочках. Распределенную невязку полигона подчеркиваем (в дальнейшем не используем). 7. В следующем полигоне значение исходной невязки изменится на величину поправки, пришедшей из предыдущего полигона.8. Новую невязку распределяем по звеньям пропорционально красным числам. Распределенную невязку подчеркиваем и так далее по ходу. 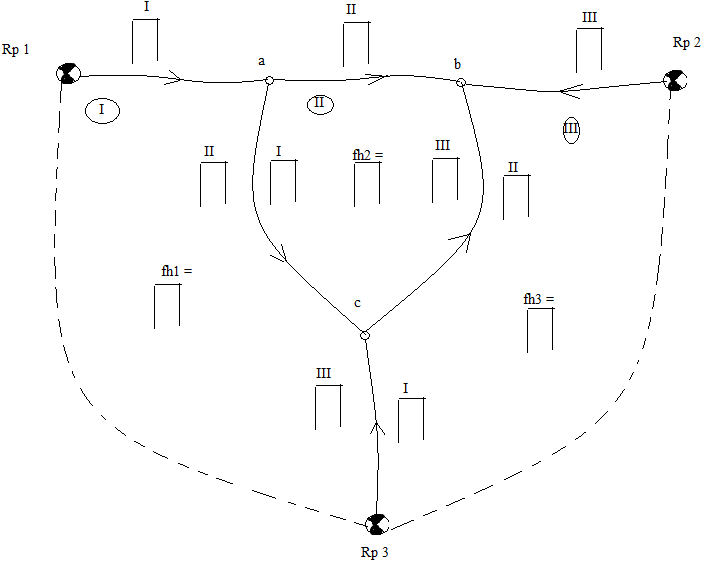 Рисунок 7. Схема уравнивания несвободной нивелирной сети способом «красных чисел» 5.5. ВЫЧИСЛЕНИЕ УРАВНЕННЫХ ЗНАЧЕНИЙ ПРЕВЫШЕНИЙ И ОТМЕТОК УЗЛОВЫХ ТОЧЕК И ОЦЕНКА ТОЧНОСТИ РЕЗУЛЬТАТОВ УРАВНИВАНИЯЗАДАЧА: Произвести вычисления поправок на звенья каждого полигона, считая направления звеньев совпадающими с направлением обхода полигона (Рисунок 7). ПОРЯДОК РЕШЕНИЯ: 1. При вычислении поправок на звенья каждого полигона следует руководствоваться следующими правилами: - для внешнего звена i-го полигона поправка на звено νi равна сумме Si внешней таблички этого звена с обратным знаком, т. е. νi = Si. Для звеньев смежных полигонов поправка νij равна разности сумм чисел внутренней и внешней табличек этого звена, т. е νij = Sij – Sji Полученные поправки записываем около соответствующих звеньев; у внутренних (смежных) звеньев поправки записываем по обе стороны звена. Контролем уравнивания сети является выполнение условия: в каждом полигоне сумма поправок на звенья должна равняться невязке полигона с обратным знаком. 2. После введения вычисленных поправок в превышения по звеньям получаем исправленные (уравненные) их значения как: hiиспр. = hiизмер. + νi 3. По исправленным значениям превышений вычисляем отметки узловых точек по формуле: Hi = Hисх.+ hiиспр. Результаты вычислений сводим в Таблицу Вычисление уравненных значений превышений и отметок узловых точек. Таблица 3. Вычисление уравненных значений превышений и отметок узловых точек
Выполнение оценки точности нивелирной сети IV класса способом ЗАДАЧА: Выполнить оценку точности нивелирной сети IV класса по поправкам, к измеренным превышениям, приведенным в практическом занятии № 10 ПОРЯДОК РЕШЕНИЯ: Точность определения отметок точек сети, уравненной по способу В. В. Попова, характеризуется средней квадратической погрешностью нивелирования на 1 км хода по формуле: m1 км = 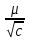 μ = 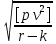 где ν – поправки по звеньям; p = 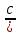 – вес превышения по i звену; ni – длина звена, км; с – длинна нивелирного хода, вес которого принят равным единице; r – число нивелирных звеньев; к – число полигонов. Таблица 4. Оценка точности результатов уравнивания
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||