Практическое_задание_2. Визуализация многомерных данных. Введение в Matplotlib
 Скачать 1.05 Mb.
|
Способы визуализации описательных статистик для числовых призна-ков Если признаков много, то можно строить для каждой описательной стати-  стики точечныйилистолбчатыйграфики. Пример такого графика дан на ри- сунке 2, лучше всего его использовать для большого числа параметров.Рисунок 2 – Точечный график выборочного среднего для множества параметровДанные графики рекомендуется упорядочить по значению величины, чтобы вы- делить похожие группы параметров. Выделение таких групп позволит исключить признаки из дальнейшего анализа. Если для визуализации описательных стати- стик используется несколько графиков (миниатюры), следите за тем, чтобы поря- док признаков по оси X был скоординирован, т.е. недопустима ситуация, когда признаки на разных графиках упорядочены по-разному, т.к. это может привезти к ложным выводам. Для визуализации множества описательных статистик могут быть использо- ваны специальные методики визуализации, такие как «ящик с усами» (box plot), скрипичная диаграмма (violin plot). Схемы визуализации «ящика с усами» и скрипичной диаграммы (violin plot) представлены на рисунке 3. Они в удобной форме показывают медиану (или, если нужно, среднее), нижний и верхний квар- тили, минимальное и максимальное значение выборки и выбросы. Методика визуализации «Ящик с усами» был предложен Дж. Тьюки в 1970. Несколько таких ящиков можно нарисовать бок о бок, чтобы визуально сравни- вать одно распределение с другим; их можно располагать как горизонтально, так и вертикально. Расстояния между различными частями ящика позволяют опреде- лить степень разброса (дисперсии) и асимметрии данных и выявить выбросы. 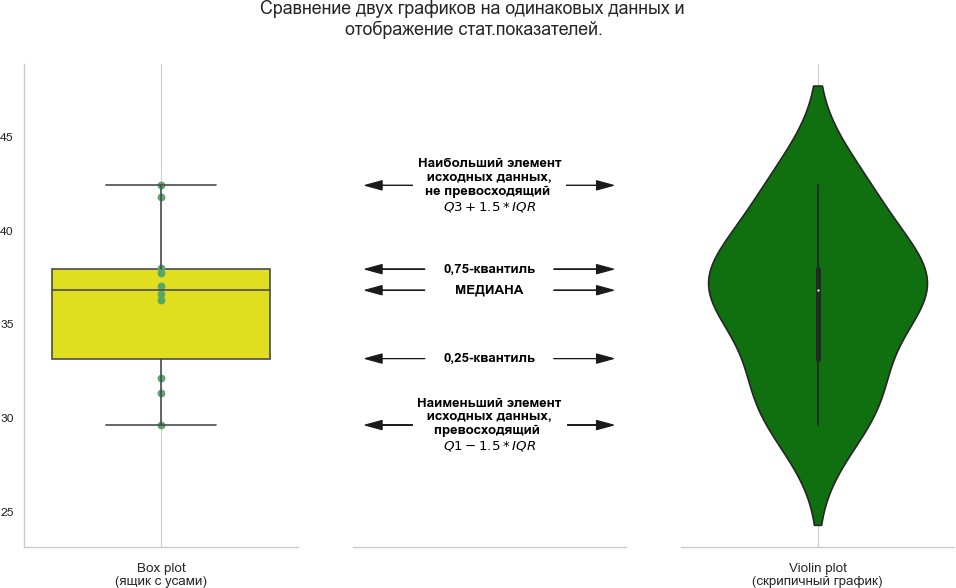 Рисунок 3 – Схема диаграммы ящик с усами (Box Plot) искрипичнойдиаграммы(Violin Plot)[Грошев,2020] Скрипичная диаграмма похожа на диаграмму «ящик с усами» за исключе- нием того, что они также показывают плотность вероятности данных при различ- ных значениях, обычно сглаженную с помощью ядерной оценки плотности. Плот- ность распределения - это границы графика «скрипки», она позволяет увидеть, распределены ли данные равномерно или есть несколько центров, где значения встречаются более часто. В этом случае график скрипки показывает наличие раз- личных пиков, их положение и относительную амплитуду. Как правило, скрипич- ная диаграмма включает все данные, которые есть на диаграмме «ящик с усами»: маркер для медианы данных; рамка или маркер, указывающий на интерквартиль- ный размах; и, возможно, все точки выборки, если количество выборок не слиш- ком велико. Несмотря на то, что график скрипки является более информативным, чем обычный «ящик с усами», он является менее популярным, и как результат, он менее понятен пользователям. Общим недостатком, свойственным для ящика с усами (box plot) и скрипич- ной диаграммы (violin plot) является сложность сравнения отдельных значений, например медианы для множества признаков. На рисунке 4 представлен пример использования ящика с усами для сравнения доходов в зависимости от рода заня- тости и пола. Очевидно, что в данном случае выбор графика не идеален. Во-пер- вых, сравнение в рамках одного типа занятий между представителями разных по- лов затруднен, проще выполнять сравнение доходов для представителей одного пола. Другим явным недостатком является достаточно большой разброс значений из-за выбросов. Возможным решением было бы использование трансформации значений признаков (например, применяя операцию логарифмирования к исход- ному множеству значений признаков). На рисунке 5 напротив представлено до- статочно удачно решение по использованию диаграммы «ящик усов», с его помо- щью легко установить паттерны потребления электроэнергии в зависимости от дня недели и времени года. 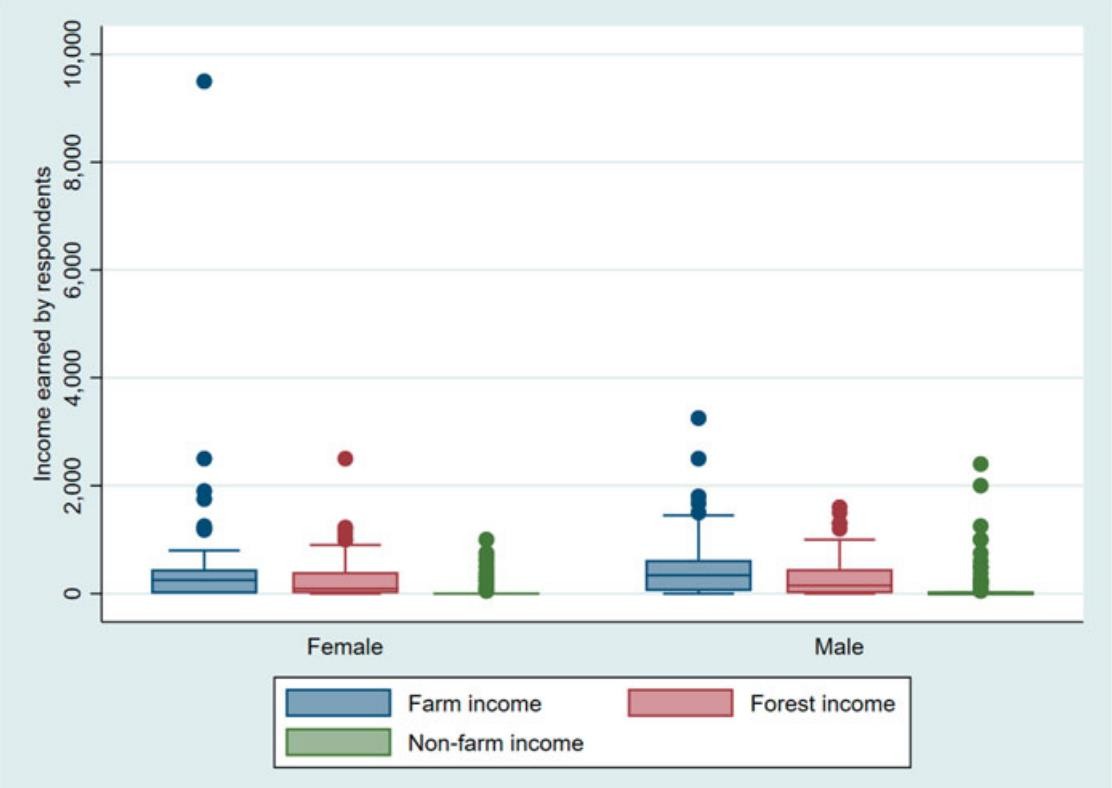 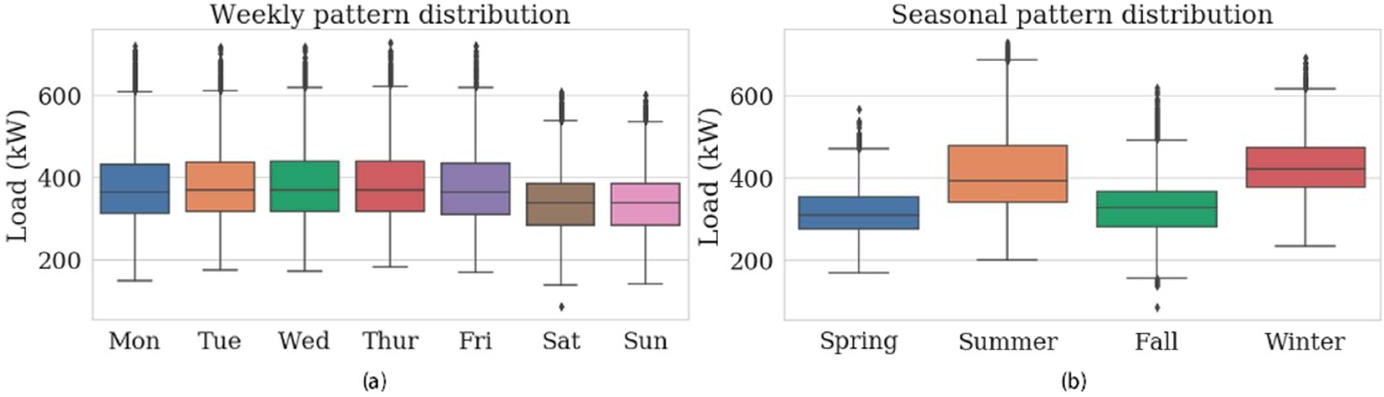 Рисунок 4 - Сравнительная диаграмма "ящик с усами, показывающая распределение дохода взависимости от половой принадлежности [Nhem etal., 2018]Рисунок 5 – Сравнительная диаграмма распределения нагрузки в зависимости от (а) сезона и(б)днянедели. [Leeet al. 2019] Кроме ящика с усами (box plot) и скрипичной диаграммы (violin plot) для оценки распределения значений признака следует использовать гистограммы. Гистограмма – это наглядное представление функции плотности вероятности не- которой случайной величины, построенное по выборке. Иногда её называют ча- стотным распределением, так как гистограмма показывает частоту появления из- меренных значений параметров объекта. Данное понятие и название для него вве- дены Карлом Пирсоном в 1895 году. Гистограмма строится следующим образом. Сначала множество значений, которое может принимать элемент выборки, разби- вается на несколько интервалов (корзинок, bins). Чаще всего эти интервалы берут одинаковыми, но это не является строгим требованием. Эти интервалы отклады- ваются на горизонтальной оси, затем над каждым рисуется прямоугольник. Если все интервалы были одинаковыми, то высота каждого прямоугольника пропорци- ональна числу элементов выборки, попадающих в соответствующий интервал. Если интервалы разные, то высота прямоугольника выбирается таким образом, чтобы его площадь была пропорциональна числу элементов выборки, которые по- пали в этот интервал. С помощью гистограмм можно оценить распределение значений каждого признака атрибута, выявить наиболее часто принимаемые значения, оценить их правдоподобность. Таким образом, можно обнаружить выбросы, значения по умолчанию, выявить интересные закономерности, связанные непосредственно с предметной областью. При этом рекомендуется экспериментировать с настрой- ками самого графика – менять число интервалов («корзинок»), ширину столбцов. На рисунке 6 показано, каким образом меняется информация о данных при изме- нении числа «корзинок» - в случае увеличения числа становится заметна волно- образная зависимость в распределении значений анализируемого атрибута. 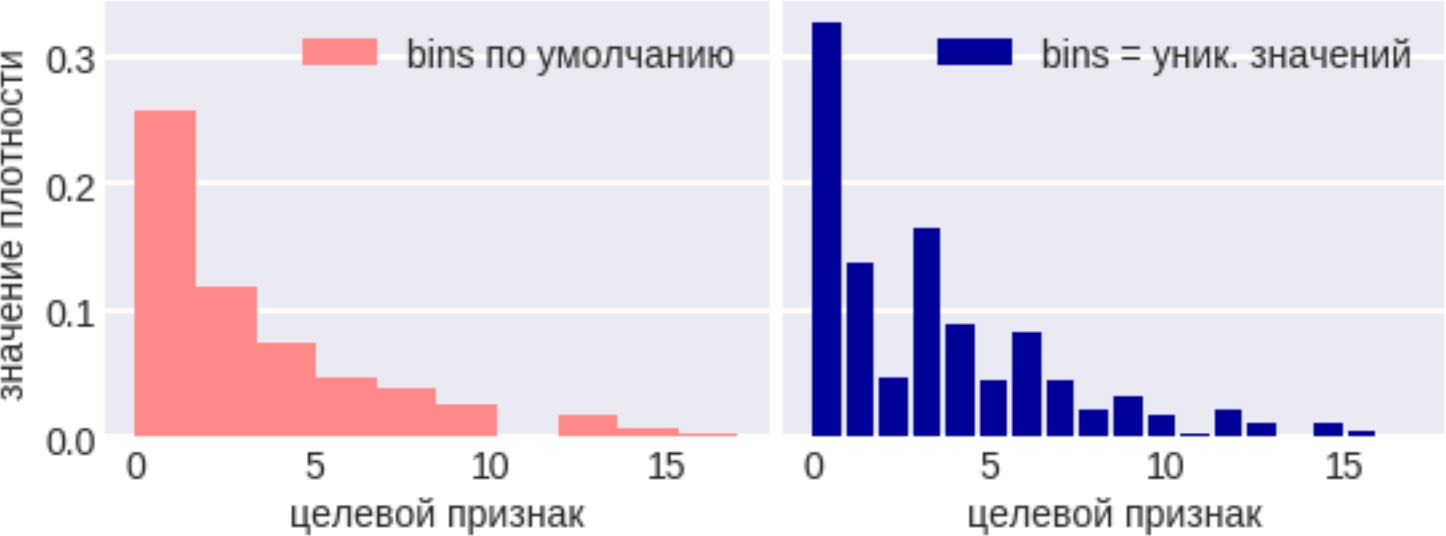 Рисунок 6 – Влияние настроек параметров гистограммы на результаты анализа [Дьяконов,2020] Для решения задачи оценки распределения значений также могут быть ис- пользованы графики плотностей распределения. Однако следует отметить, что ис- пользование гистограмм более предпочтительно, т.к. они могут «вскрыть» неко- торые эффекты, которые не столь заметны на графики плотности в силу большей «сглаженности» графика плотности. 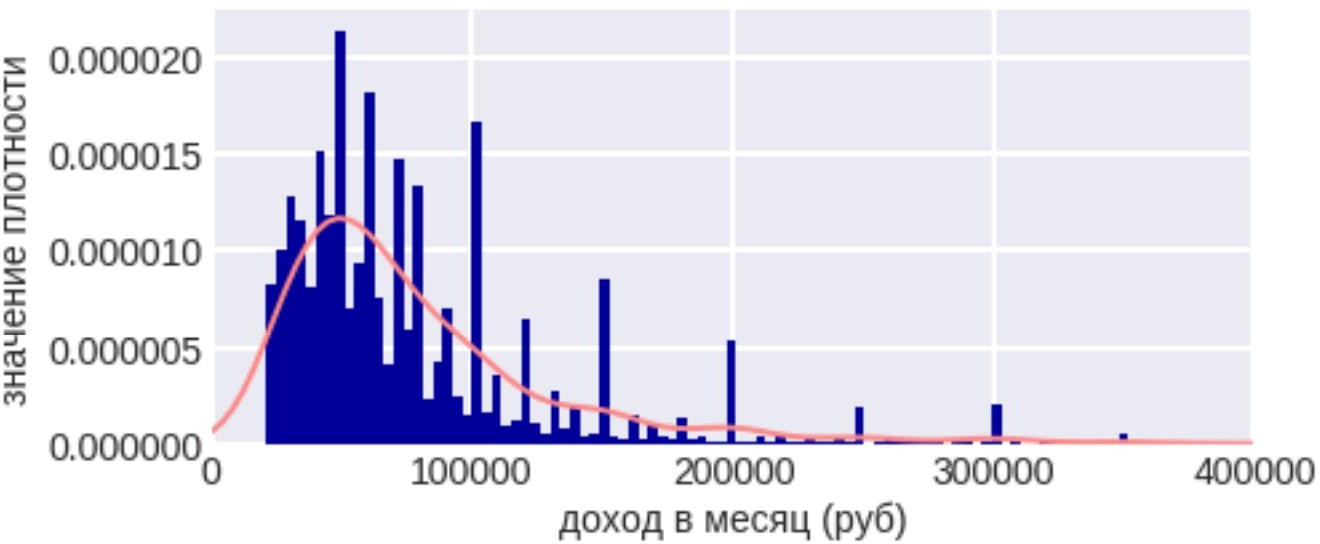 Рисунок7-Плотностьигистограммаатрибута«Доходвмесяц»[Дьяконов2020] Если решается задача машинного обучения, и в данных присутствует целе- вой атрибут, то рекомендуется оценить, как распределены значения атрибутов с учетом значения целевого атрибута, а также сравнить распределения значений на обучающей и на тестовой выборках, это значительно упростить задачу анализа полученных результатов. Так, например, если данные на обучающей и на тесто- вой выборке распределены не одинаково, то значение оценок качества машинного обучения будут не высоки, и в этом случае стоит проанализировать возможные методики трансформации данных для получения новых признаков, которые будут иметь одинаковое распределение на тестовых и обучающей выборке. При визуализации значений как описательных статистик, так и непосред- ственно значений признаков, помните про области значений разных атрибутов. Различие в размахе значений может привезти к тому, что некоторые зависимости могут быть незаметны. Кроме того, помимо масштабирования можно использо- вать прием деформации признака, например, выполнять логарифмирование его значений. При визуализации больших объемов данных, особенно в случае данных от киберфизических объектов, следует разбивать данные на части, например, с уче- том временной метки, увеличивая тем самым масштаб по оси времени (или числу отображаемых объектов). Это позволит выявить не только цикличность в данных, но и возможные переходные процессы, связанные, например, с выходом системы на определенные режимы. В последнее время принято данные с переходными процессами исключать из обучающей выборки, если целью не является выявле- ние этих процессов. Такое решение позволяет повысить качество машинного обу- чения. На рисунке 8 представлено изменение признака во времени, и очевидно, что система выходит на режим после 600 отсчета времени, следовательно, первые 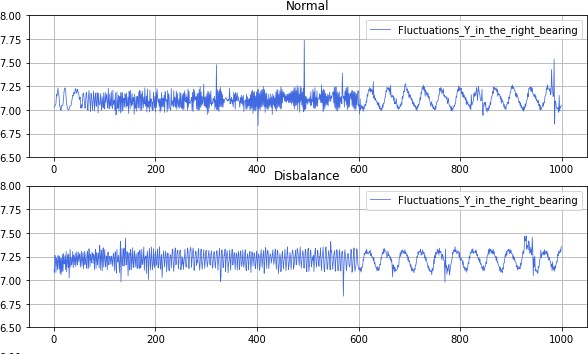 600 записей могут быть исключены из анализа. С другой стороны, если на этом этапе уже очевидны определенные изменения в поведении системы, то такие дан- ные могут быть использованы для раннего их обнаружения.Рисунок 8 – Линейные графики параметра для нормального (верхний график) и аномального(нижнийграфик)состояниясистемы. Для визуализации номинальных параметров выбор возможных вариантов графиков не столь велик. В основном используется столбчатая диаграмма, от- ражающая число записей с заданным типом значения. (Не путать с гистограм- мой!). Если возможно, параметры следует упорядочивать по возрастанию, если это не нарушает внутреннюю логику данных. Например, на рисунке 9 представ- лен столбчатая диаграмма, характеризующая частоту встречаемости bash команд в системных логах, на рисунке 9а он не упорядочены по встречаемости, а на ри- сунке 9б – они упорядочены по убыванию, и выполнять задачи сравнения уже значительно проще (определите с помощью графика 9а, какая команда чаше ис- пользуется grep или sudo?). Множество категории с небольшими значениями можно объединять в одну категорию «другое».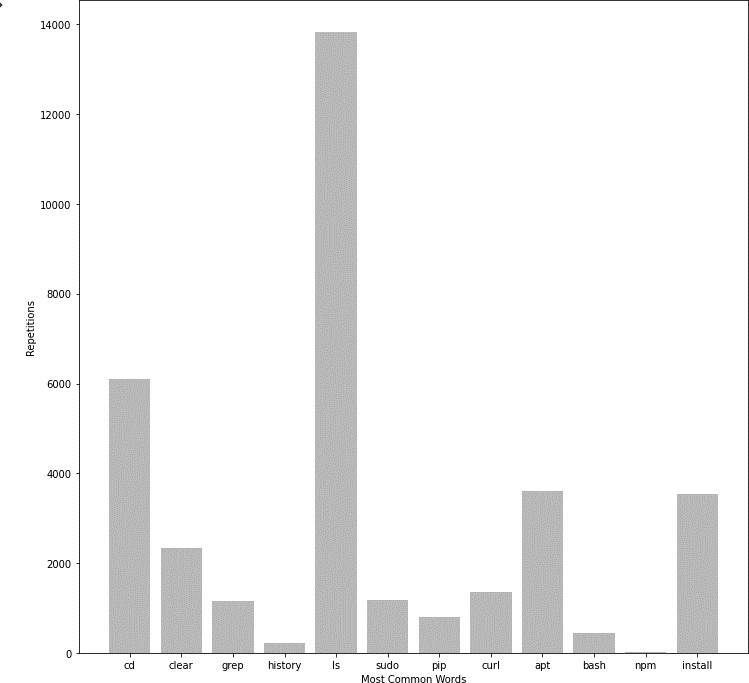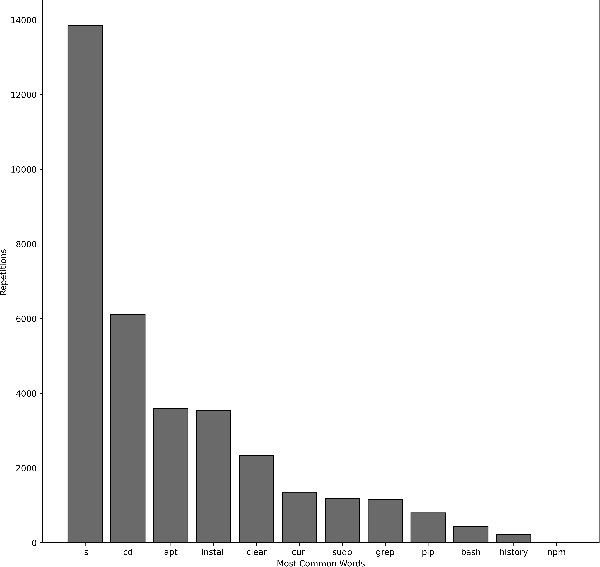  
Рисунок 9 – Столбчатые диаграммы: а) данные не упорядочены по значению, б) данныеупорядочены по убыванию. |