Практическое_задание_2. Визуализация многомерных данных. Введение в Matplotlib

• Название: Визуализация многомерных данных. Введение в Matplotlib
• Дата: 08.03.2023
• Размер: 1.05 Mb.
• Имя файла: Практическое_задание_2.docx
• Тип: Документы; #974604
• страница: 4 из 9

Анализ данных методами визуализации

Одномерный анализ данных

Одномерный анализ (univariate analysis) – представляет собой исследование отдельных атрибутов (или признаков), представленных в наборе данных. Основ- ной целью такого анализа является понимание природы данных и выявление осо- бенностей в них.

Понимание природы данных связано с определением следующих характери- стик признака:

• 
  имя
  
• 
  область значений
  
• 
  распределение значений
  
• 
  выявление аномалий (выбросов), пропусков и т.д.
  

Если при визуальном анализе выявляется что-то странное, то такие «странности» могут быть использованы в последующем анализе данных.

Исходными данными для визуализации в этом случае служат:

• 
  непосредственно значения атрибута
  
• 
  описательные статистики признаков
  
• 
  характеристики признаков (например, их важность)
  

Перечислим основные статистики, которые описывают выборку.

Пусть Х₁, Х₂ ... X_n - выборка независимых случайных величин. Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:

Х₍₁₎ < Х₍₂₎ < ... < X_(n) .

Тогда размахом выборкиRназывается величина: R= X_(n) - X_(1), т.е. размах это расстояние между максимальным и минимальным членом вариационного ряда.

Выборочноесреднееравно: 𝑋^̅ = ^∑𝑛

𝑋_𝑖.

𝑖=1

𝑛

Выборочным оно называется потому что вычисляется для заданной выборки, и может быть разным для разных выборок.

Медианаделит ряд упорядоченных значений пополам с равным числом этих значений как выше, так и ниже ее (левее и правее медианы на числовой оси). Вы- числить медиану легко, если число наблюдений n нечетное. Это будет наблюде- ние номер (n+ 1)/2 в упорядоченном наборе данных. Если nчетное, то, строго го- воря, медианы нет. Однако обычно она вычисляется как среднее арифметическое двух соседних средних наблюдений в упорядоченном наборе данных (т. е. наблю- дений номер (n/2) и (n/2 + 1)).

Мода— это значение, которое наиболее часто встречается в наборе данных; если данные непрерывные, то мы обычно группируем их и вычисляем модальную

группу. Некоторые наборы данных не имеют моды, потому что каждое значение встречается только 1 раз. Иногда бывает более одной моды; это происходит тогда, когда 2 значения или больше встречаются одинаковое число раз и встречаемость каждого из этих значений больше, чем любого другого значения.

Также к описательным статистикам относятся такие характерные элементы как минимум, максимум и квантили.

Квантиль– значение, которое случайное величина не превышает с заданной вероятностью. Наиболее часто используемые квантили:

• 
  0,25-квантиль называется первым (или нижним) кварти_́ лем (от лат. quarta — четверть);
  
• 
  0,5-квантиль называется медианой (от лат. mediāna — середина) или вторым кварти_́ лем;
  
• 
  0,75-квантиль называется третьим (или верхним) кварти_́ лем.
  

Интеркварти_́ льным размахом (англ. Interquartile range) называется раз- ность между третьим и первым квартилями, то есть x_0.75 – x_0.25. Следует отметить, что интерквартильный размах является характеристикой разброса распределения

величины и является робастным аналогом дисперсии. Вместе, медиана и интерк- вартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозмож- ности вычисления последних.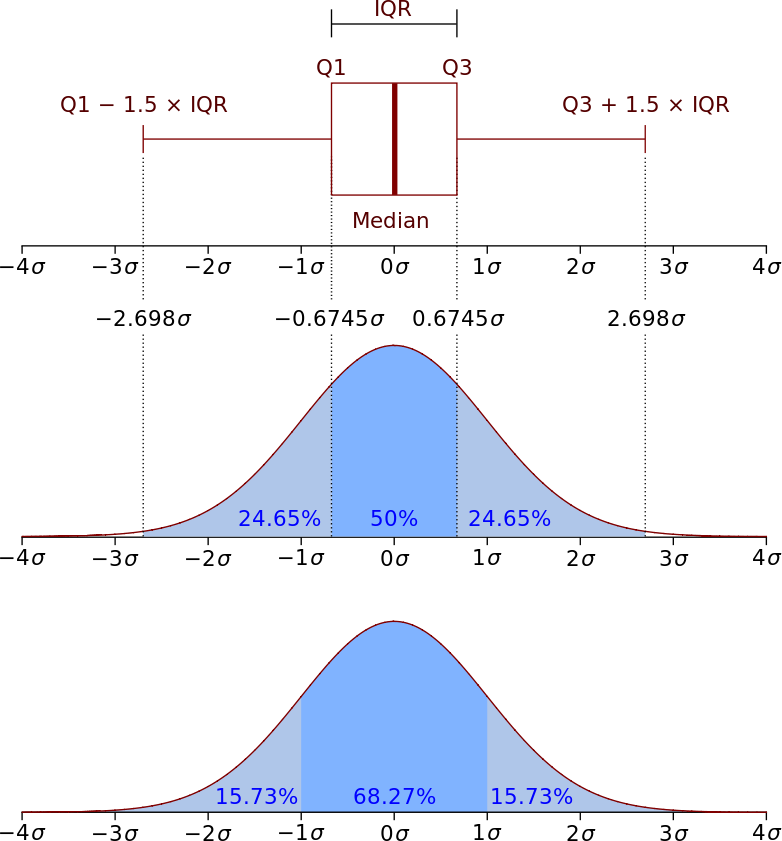


Рисунок1–Квантилинормальногораспределения

Для оценки разброса в данных используется дисперсия. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений. Дис- персия Dслучайной величины вычисляется как:

2

^∑𝑛 (𝑋 − 𝑋^⃐ )

𝐷 = 𝜎² =

𝑖=1 ^𝑖

𝑛

В случае выборки, выборочная дисперсия вычисляется как:

_∑𝑛

⃐̅ ²

𝑠² =

_𝑖=1(𝑋_𝑖−𝑋) _.

𝑛−1

Среднеквадратическое отклонение — это положительный квадратный корень из дисперсии, соответственно, стандартное отклонение выборки - корень из выборочной дисперсии:

_∑𝑛

⃐̅ ²

𝑠 = ^√

_𝑖=1(𝑋_𝑖−𝑋) _.

𝑛−1

Cтандартное отклонение можно трактовать как своего рода среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что

и исходные данные. Если разделить стандартное отклонение на среднее арифме- тическое и выразить результат в процентах, получится коэффициентвариации.