Практическое_задание_2. Визуализация многомерных данных. Введение в Matplotlib
 Скачать 1.05 Mb.
|
Многомерный анализ данныхВ случае многомерного анализа данных выполняется анализ 2 и более перемен- ных. Отметим, что в задачах машинного обучения визуализировать можно не только пары признаки, но пары «признак-целевой атрибут», а также «алгоритм (результат его работы)-признак» и «алгоритм1 (результат его работы)- алгоритм2 (результат его работы)», это позволит выбрать оптимальный алгоритм и его настройки для решаемой аналитической задачи. Наиболее распространённый способ визуализации является диаграммарас-сеяния(scatterplot). Диаграмма рассеяния отображает значения двух переменных в виде точек на декартовой плоскости, могут использоваться и полярные коорди- наты, особенно в случаях, когда одна из переменных представляет собой физиче- ское направление или имеет циклический характер. С ее помощью можно уви- деть: наличие корреляции (линейной зависимости) при малом шуме и правильно выбранном масштабе; наличие зависимости при малом шуме и «достаточно равномерном» распре- делении; кластеры (при правильном масштабе); выбросы (при правильном масштабе); типичные значения (но затруднительно при большом объеме данных).  В некоторых случаях можно сделать выводы о независимости значений ат- рибутов, но такой вывод может быть ложным при наличии сложных нелинейных зависимостях.Рисунок9.Диаграммарассеяния[Дьяконов,2020] Попарное сравнение признаков процесс достаточно ресурсоемкий, его можно выполнять, если есть время, а можно визуализировать потенциально инте- ресные сочетания, например, пары наиболее значимых признаков. Например, на рисунке 10 при визуализации пары (sepal_length, sepal_width) классы Versicolor и Virginica «перемешивают» и сложно разделимы, а в случае визуализации пары (sepal_length, petal_width) все классы хорошо разделимы. Таким образом, именно эти признаки являются «хорошими», и могут быть использованы в задаче класси- фикации. Выбросы при хорошей разделимости классов заслуживают отдельно внимания, они могли возникнуть как в результате каких-либо ошибок сбора дан- ных, а могут являться примерами нового класса. 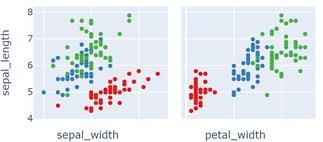  Рисунок 10 – Диаграмма рассеяния пар параметров (sepal_length, sepal_width) и (sepal_length,petal_width) Диаграмма рассеяния хорошо также тем, что позволяет дополнительно визу- ализировать 1-2 признака, если их закодировать цветом, размером или формой. Однако такое решение хорошо лишь работает на не больших выборках данных. Другим способом визуального анализа связей между признаками является матрица корреляции. Матрица корреляции представляет собой квадратную таб- лицу, которая показывает коэффициенты корреляции между несколькими пере- менными. Коэффициент корреляции между двумя случайными величинами Xи Yвычисляется следующим образом: 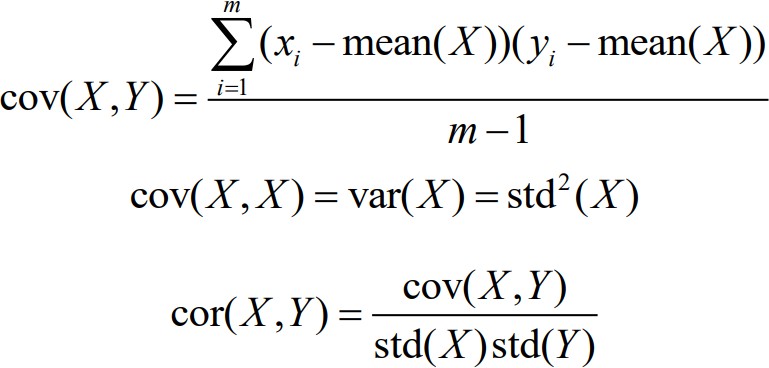 Коэффициент корреляции имеет значение от -1 до 1, где: -1 указывает на сильную отрицательную линейную корреляцию между двумя переменными 0 указывает на отсутствие линейной корреляции между двумя переменными 1 указывает на сильную положительную линейную корреляцию между двумя переменными. В заключение следует отметить, что очень часто бывает полезно визуализировать служебные данные, такие как номер строки, или категория данных (обучающая выборка, тестовая), т.к. в некоторых случаях можно увидеть интересные законо- мерности или факты, которые были не очевидны. |