ВСР. Внеаудиторная самостоятельная работа
 Скачать 1.26 Mb.
|
|
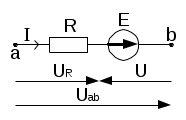
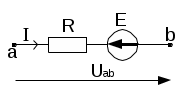
Министерство образования и науки Алтайского края краевое государственное бюджетное профессиональное образовательное учреждение «Рубцовский аграрно-промышленный техникум» ______________________________________________________________________________ наименование учебной дисциплины ВНЕАУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА _________________________________________________ (наименование: реферат, доклад, практическая работа и др.) ______________________________________________________________________________________________ фамилия, имя, отчество студента ______________________________________________________________________________________________ (специальность) ______________________________________________________________________________________________ фамилия, имя, отчество преподавателя ______________________________________________________________________________________________ подпись преподавателя Группа ________________________ Самостоятельная работа №1 Тема 1.1 Электрическое поле Электрическое поле (статическое) — поле неподвижных, электрически заряженных тел, заряды которых не изменяются во времени. Электрическое поле обнаруживается как силовое взаимодействие заряженных тел. При этом различают положительные и отрицательные заряды. (виды зарядов) Заряды одного знака отталкиваются друг от друга, разного знака притягиваются. (взаимодействие зарядов) В основе описания свойств электрического поля лежит закон Кулона, установленный опытным путем. Закон Кулона. Между покоящимися точечными зарядами действует сила, пропорциональная произведению зарядов, обратно пропорциональная квадрату расстояния между ними и направленная по прямой от одного заряда к другому (рис. 1.): 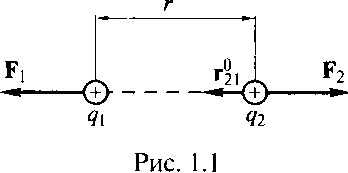 Рисунок 1 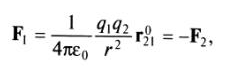 где F — сила, действующая на заряд q r2 — квадрат расстояния между зарядами q1 и q2 F2 — сила, действующая на заряд q2 r021 — единичный вектор, направленный от второго заряда к первому; е0 = 8,854 • 10-12 Ф/м — электрическая постоянная. Точечными зарядами можно считать заряженные тела, размеры которых малы по сравнению с расстоянием между ними. Основные единицы измерения: силы в международной системе единиц (СИ) — ньютон (Н); заряда — кулон (Кл): 1 Кл = 1 А • с; длины — метр (м). Основными величинами, характеризующими электрическое поле, являются напряженность, электрический потенциал и разность потенциалов, или напряжение Напряженностью электрического поля называется мера интенсивности его сил, равная отношению силы F, действующей на пробный положительный точечный заряд q, вносимый в рассматриваемую точку поля, к значению заряда: 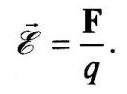 Так же как и сила F, напряженность электрического поля ε — векторная величина, т.е. характеризуется значением и направлением действия. Основная единица измерения напряженности электрического поля в СИ — вольт на метр (В/м). Из формулы (1.1) следует, что напряженность электрического поля точечного заряда q на расстоянии r от него равна 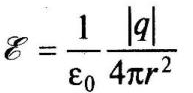 и направлена от точки расположения заряда к точке, где определяется напряженность, если заряд положительный (рис. 2, а),  Рисунок 2, а и в противоположную сторону, если заряд отрицательный (рис. 2, б). 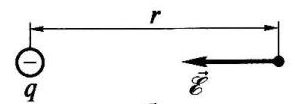 Рисунок 2, б Если зарядов, создающих электрическое поле, несколько, то напряженность в любой точке поля равна геометрической сумме напряженностей от каждого из них в отдельности. (напряженность электростатического поля нескольких зарядов). Самостоятельная работа №2 Тема 1.2 Электрические цепи постоянного тока Электрические цепи постоянного тока – цепи, в которых протекает электрический ток, не изменяющийся во времени ни по величине, ни по направлению. В электрических цепях действуют следующие основные законы: закон Ома и I и II законы Кирхгофа Закон Ома. а) Закон Ома для участка цепи без источника. Сила тока на участке электрической цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению этого участка (рис. 1): 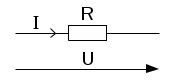  Рис. 1 б) Обобщенный закон Ома (для участка цепи с ЭДС) (рис. 2):
Если направление тока в ветви совпадает с направлением ЭДС источника (рис. 4а), то     .Если направление тока в ветви не совпадает с направлением ЭДС источника (рис. 4б), то  .Законы Кирхгофа (рис. 3). а 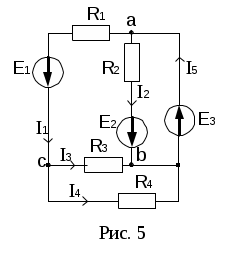 ) I закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю, при этом токи, одинаково направленные относительно узла, записываются с одинаковым знаком. Для узла а:  .б) II закон Кирхгофа: алгебраическая сумма падений напряжений любого контура равна алгебраической сумме ЭДС этого контура. Правило знаков: падения напряжения записываются со знаком «+», если направления тока совпадает с направлением обхода контура; ЭДС записываются со знаком «+», если направления ЭДС и обхода контура совпадают. Рассмотрим схему электрической цепи, приведенную на рис. 3. Направление обхода контура abca выберем по часовой стрелке. Тогда уравнение II закона Кирхгофа будет иметь следующий вид:  .Баланс мощности. Мощность характеризует интенсивность преобразования энергии одного вида в другой за единицу времени. Для цепи постоянного тока мощность источника:  а приемника -  , ( =Вт). На основании закона сохранения энергии мощность, развиваемая источниками электроэнергии, должна быть равна сумме мощностей всех приемников и потерь в источниках из-за внутренних сопротивлений. При этом: если направление ЭДС и тока совпадают, то EI в сумме записываются со знаком «+». Для схемы рис. 5 при выбранных направлениях токов: .Самостоятельная работа №3 Тема 2.2 Правила Кирхгофа. Расчет сложных электрических цепей Чтобы расчеты сложных электрических цепей с неоднородными участками не вызывали трудности, существует упрощение с помощью применения правил Кирхгофа, которые рассматривают как обобщение закона Ома на случай разветвленных цепей. В таких цепях выделяют узловые точки, называемые узлами, где сходятся не менее трех проводников, как изображено на рисунке 1. Токи, поступающие в узел, считают положительными, а вытекающие – отрицательными. 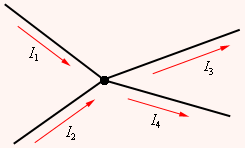 Рисунок 1. Узел электрической цепи. I1, I2>0; I3, I4<0I1, I2>0; I3, I4<0. В узлах цепи с постоянным током не происходит накопление зарядов. Получаем первое правило (закон) Кирхгофа: Алгебраическая сумма сил токов для каждого узла разветвленной цепи равняется нулю: I1+I2+I3+...+In=0I1+I2+I3+...+In=0. Наличие разветвленной цепи позволяет выделить несколько замкнутых путей, которые состоят из однородных и неоднородных участков. Их принято называть контурами. На участках с выделенным контуром могут протекать различные токи. Рисунок 2 наглядно показывает пример такой цепи, соответствующей 11 закону Кирхгофа. Она состоит из двух узлов aa и dd, в которых сходятся одинаковые токи. Только один из заданных узлов будет независимым. 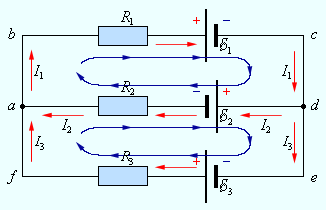 Рисунок 2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (aa или dd) и два независимых контура (например, abcd и adef) В предложенной цепи выделяют три контура вида abcd, adef и abcdef. Независимыми считаются только два: abcd и adef. Последний из вышеперечисленных не имеет никаких новых участков. Второе правило Кирхгофа – это следствие обобщенного закона Ома. Для записи обобщенного закона Ома участков, составляющих один из контуров цепи, используется пример, изображенный на рисунке 2 для abcd. Каждому участку задаются положительные направления тока и обхода контура. Для записи следует учитывать «правила знаков», приведенные на рисунке 3. 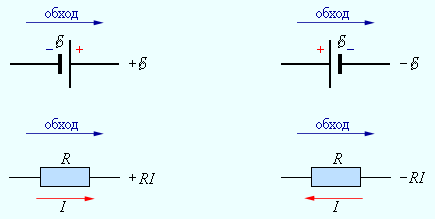 Рисунок 3. «Правила знаков» Запись обобщенного закона Ома для участков контура abcdabcd принимает вид: Для bcbc: I1R1=Δφbc−δ1I1R1=∆φbc-δ1. Для dada: I2R2=Δφda−δ2I2R2=∆φda-δ2. Сумма левых и правых частей равенств с условием Δφbc=−Δφda∆φbc=-∆φda преобразует выражение: I1R1+I2R2=Δφbc+Δφda−δ1+δ2=−δ1−δ2I1R1+I2R2=∆φbc+∆φda-δ1+δ2=-δ1-δ2. Таким же образом можно записать для adefadef контура: −I2R2+I3R3=δ2+δ3-I2R2+I3R3=δ2+δ3. 2 правило или закон Кирхгофа: алгебраическая сумма сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока этого участка равняется сумме ЭДС вдоль этого контура. Оба правила Кирхгофа для всех узлов и контуров разветвленной цепи дают необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов электрической цепи. Цепь, изображенная на рисунке 2, рассматривается как система уравнений для определения трех неизвестных I1, I2I1, I2 и I3I3: I1R1+I2R2=−δ1−δ2I1R1+I2R2=-δ1-δ2, −I2R2+I3R3=δ2+δ3-I2R2+I3R3=δ2+δ3, −I1+I2+I3=0-I1+I2+I3=0. То есть применение этих правил помогает свести расчет электрической цепи постоянного тока к решению системы. Процесс не вызывает трудностей, но зачастую приходится работать с громоздкими выражениями простых цепей. При получении отрицательного значения силы тока на участке цепи говорят о противоположном направлении тока, относительно выбранного. Самостоятельная работа №4 Тема 2.3 Однофазные электрические цепи синусоидального напряжения Электрическая цепь синусоидального тока содержит помимо электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и т.д.), также устройства, присущие только цепям синусоидального тока: трансформаторы, конденсаторы, катушки индуктивности и др. Напряжения и токи в цепях синусоидального тока зависят от времени. Они называются мгновенными значениями и обозначаются строчными буквами: u и i. Элементами схем замещения цепей синусоидального тока являются источники синусоидального (ЭДС) тока, резистивные R, индуктивные L и емкостные С элементы. Указанные элементы отображают физические процессы, протекающие в устройстве. Резистор отображает на схеме замещения необратимые процессы преобразования электрической энергии в другие виды энергии (лучистую, тепловую, механическую). Катушка индуктивности отображает процессы преобразования электрической энергии в энергию магнитного поля, а также явления, связанные с этим преобразованием (явление самоиндукции и взаимоиндукции). Конденсатор на схеме замещения характеризует процессы преобразования электрической энергии в энергию электрического поля, а также явления, связанные с этим преобразованием (явление заряда и разряда конденсатора). Промышленными источниками синусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых и гидравлических турбин преобразуется в электрическую. Принципиальная конструкция простейшего электромеханического генератора содержит неподвижный, плоский разомкнутый виток с выводами а и в и постоянный магнит, который вращается с постоянной частотой f, т.е. с постоянной угловой частотой 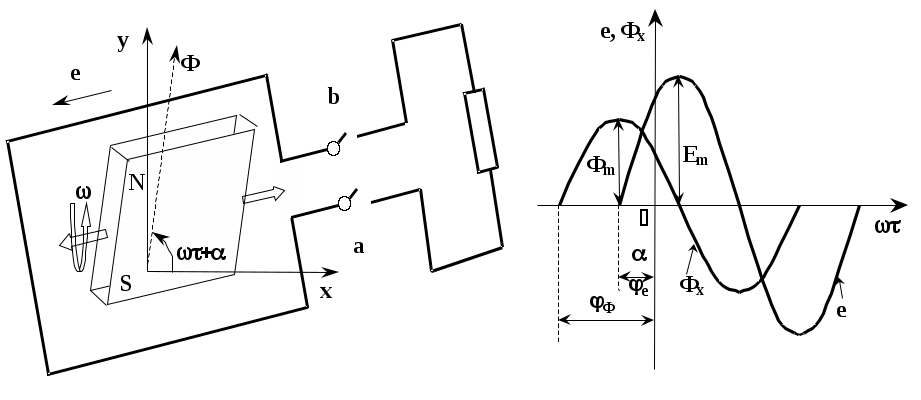 , внутри витка. Основная единица частоты в системе СИ – герц (Гц). Величина обратная частоте называется периодом  , измеряется в секундах (с).Синусоидальные величины принято изображать графически в виде зависимости  . Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат, т.е. от  .Если начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат. Если к выводам «а» и «в» генератора подключить резистор, то в полученной цепи возникнет синусоидальный ток i. Самостоятельная работа №5 Тема 2.4 Трехфазные электрические цепи Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке. Таким образом, понятие «фаза» имеет в электротехнике два различных значения: фаза как аргумент синусоидально изменяющейся величины; фаза как составная часть многофазной электрической системы. Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений. Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О. Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем. 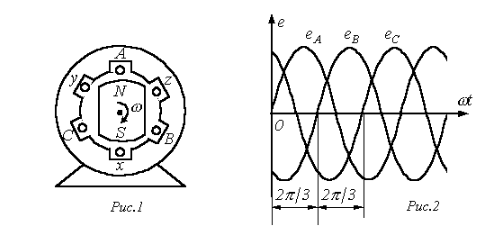 Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на 2π/3 эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы – соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на 2π/3 рад. (см. рис. 2). Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются: - экономичность передачи электроэнергии на большие расстояния; - самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором; - возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств; - уравновешенность симметричных трехфазных систем. Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы. Система ЭДС (напряжений, токов и т.д.) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол. В частности, векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3. 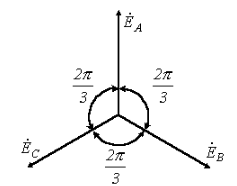 Рис. 3 Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике. Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной. Самостоятельная работа №6 | ||||
