метрология. метрология сема. Волгоградский государственный технический университет
 Скачать 35.91 Kb.
|
|
Министерство образования и науки России Федеральное государственное бюджетное образовательное учреждение высшего образования «Волгоградский государственный технический университет» Химико-технологический факультет Кафедра «Метрология, стандартизация и сертификация» Семестровая работа по Метрологии Вариант №80 Выполнил: Студент группы ХТ-342 Свотин Александр Алексеевич Проверил: кандидат технических наук, доцент Полянчикова Мария Юрьевна Волгоград, 2020 г. ЗАДАНИЕ: Провести обработку результатов равноточных многократных измерений с получением среднего арифметического значения 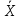 , стандартного отклонения Sx и определением суммарной погрешности измерений в виде доверительного интервала – ±ƩΔРд.Исходные данные:
Доверительная вероятность Рд = 0,97 – показывает вероятность нахождения истинного значения в рассчитанном интервале. Уровень значимости q=0,02 – показывающий, что принятый закон рассеивания размеров не будет соответствовать реальному закону. РЕШЕНИЕ 1. Построение гистограммы Определяем величину размаха R (поле рассеяния): R = Xmax – Xmin Xmax = 50,230 – наибольшее из измеренных значений Xmin = 50,970 – наименьшее из измеренных значений R = Xmax – Xmin = 0,26 (мм). Определяем число интервалов разбиения n, в соответствии с рекомендациями: k = 1 + 3,2lg(N) где N – число измерений; N = 54 k ≈ 6.54. (количество интервалов принимается ближайшим большим нечетным). Принимаем n = 7. Определяем ширину интервала h: ℎ = R/n ℎ = 0.26/7 ≈ 0,037 мм. Определяем границы интервалов 1 интервал: Xmin1 ÷ Xmax1 Xmin1 = Xmin = 50,970 мм Xmax1 = Xmin1 + h = 50,970+ 0,037 = 50,007 мм 2 интервал: Xmin2 ÷ Xmax2 Xmin2 = Xmax1 = 50,007 мм Xmax2 = Xmin2 + h = 50,007+ 0,037 = 50,044 мм 3 интервал: Xmin3 ÷ Xmax3 Xmin3 = Xmax2 = 50,044 мм Xmax3 = Xmin3 + h = 50,044 + 0,037 = 50,081 мм 4 интервал: Xmin4 ÷ Xmax4 Xmin4 = Xmax3 = 50,081 мм Xmax4 = Xmin4 + h = 50,081 + 0,037 = 50,119 мм 5 интервал: Xmin5 ÷ Xmax5 Xmin5 = Xmax4 = 50,119 мм Xmax5 = Xmin5 + h = 50,119 + 0,037 = 50,156 мм 6 интервал: Xmin6 ÷ Xmax6 Xmin6 = Xmax5 = 50,156 мм Xmax6 = Xmin6 + h = 50,156 + 0,037= 50,193 мм 7 интервал: Xmin7 ÷ Xmax7 Xmin7 = Xmax6 = 50,193 мм Xmax7 = Xmin7 + h = 50,193 + 0,037 = 50,230 мм Определяем середины интервалов Xoi: X = Xmini + h/2 1 интервал: XO1= Xmin1 + h/2 =49,970 + (0,037/2) = 49,989 (мм) 2 интервал: XO2 = Xmin2 + h/2 = 50,007 + (0,037/2) = 50,026 (мм) 3 интервал: XO3 = Xmin3 + h/2 = 50,044 + (0,037/2) = 50,063 (мм) 4 интервал: XO4 = Xmin4 + h/2 = 50,081 + (0,037/2) = 50,100 (мм) 5 интервал: XO5 = Xmin5 + h/2 = 50,119 + (0,037/2) = 50,137 (мм) 6 интервал: XO6 = Xmin6 + h/2 = 50,156 + (0,037/2) = 50,174 (мм) 7 интервал: XO7 = Xmin7 + h/2 = 50,193 + (0,037/2) = 50,211 (мм) Определение количества размеров, попадающих в каждый интервал mi Используя заданную выборку, подсчитываем количество размеров, попадающих в каждый интервал (если размер совпадает с границей интервала, то его относят в интервал, находящийся слева по числовой оси) Результаты выполненных выше расчетов занесем в таблицу:
Используя табличные данные, строим гистограмму рассеивания единичных замеров и теоретическую кривую нормального распределения:  2. Проверка выборки на соответствие нормальному закону распределения 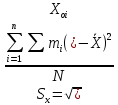 В данную формулу входит величина 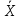, которая представляет среднее арифметическое значение измеряемой величины и определяется по формуле: После подстановки получим численные значения среднеарифметического и оценки СКО:   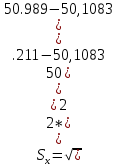 Sx=0,0499 Определение безразмерного параметра Z:  Для 1 интервала:  =  = -2,40Что соответствует величине φ(Zo1) = 0,0224 Для 2 интервала:  =  = -1,66Что соответствует величине φ(Zo2) = 0,1006 Для 3 интервала:  =  = -0,91Что соответствует величине φ(Zo3) = 0,2613 Для 4 интервала:  = =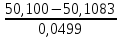 -0,17Что соответствует величине φ(Zo4) = 0,3932 Для 5 интервала:  = = 0,58Что соответствует величине φ(Zo5) = 0,3372 Для 6 интервала:  =  = 1,32Что соответствует величине φ(Zo6) = 0,1669 Для 7 интервала:  =  = 2,07Что соответствует величине φ(Zo7) = 0,0468 Определяем теоретические значения количества деталей для каждого интервала Noi. Для 1 интервала: 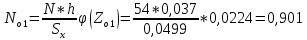 Для 2 интервала: 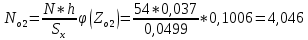 Для 3 интервала: 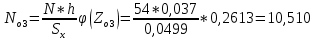 Для 4 интервала: 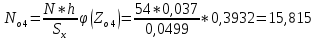 Для 5 интервала:  Для 6 интервала:  Для 7 интервала: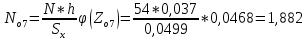 
Полученные результаты позволяют получить расчетную величину параметра хи-квадрат:  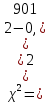  Для совпадения фактического закона распределения с теоретическим законом нормального распределения необходимо, чтобы выполнялось следующее условие:  Число степеней свободы определяется по формуле: ν = n – 1 – r ν = 7 – 1 – 2 = 4 Таким образом, табличное значение  = 7,78Так как выполняется неравенство , то можно сказать, что фактический закон распределения совпадает с теоретическим законом нормального распределения.3. Определение доверительного интервала рассеивания случайных погрешностей вокруг среднего значения Так как условие выполняется, то гипотеза о совпаденииэкспериментального и выбранного теоретического (нормального) распределения принимается (она не противоречит данным). Так как по условию Рд = 0,97, то значение функции Лапласа: Ф(Zp) = Рд/2 = 0,485. Определяем табл. величину нормированного параметра Zp, которая соответствует данному значению функции Лапласа Zp = 1,96 Таким образом, доверительный интервал случайной ошибки:  Постоянные неисключённые составляющие погрешности измерений: погрешность снятия показаний со шкалы (принимается равной 0,1 от цены деления шкалы прибора): 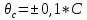  систематическая неисключенная погрешность округления результата: 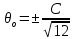 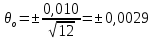 неисключенная погрешность прибора (условно принимается равной цене деления шкалы прибора): 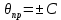 = Суммирование частных постоянных погрешностей измерения производится по двум формулам:   где k – поправочный коэффициент, зависящий от числа слагаемых погрешностей и доверительной вероятности. В нашем случае k = 0,960 Тогда:  0,001+0,0029+0,010 0,0140 мм 0,010 ммДля дальнейшего расчета выбирается наибольшее значение, т.е. принимаем  В качестве общей случайной погрешности принимаем величину доверительного интервала, полученную из экспериментов по замерам параметра:  =  0,013Определение суммарной погрешности измерения ±∆Σ: 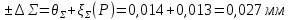 Результат в общем виде: 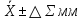 50,1083 0,02750,108 0,027 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||