Теория по линейной алгебре. Вопрос 1 Матрицы, виды матриц. Линейные операции с матрицами, свойства этих операций

• Название: Вопрос 1 Матрицы, виды матриц. Линейные операции с матрицами, свойства этих операций
• Анкор: Теория по линейной алгебре
• Дата: 14.12.2022
• Размер: 3.46 Mb.
• Имя файла: Linal.docx
• Тип: Документы; #844137

Вопрос 1: Матрицы, виды матриц. Линейные операции с матрицами, свойства этих операций.

Матрица – прямоугольная таблица чисел или любых других объектов, которые ведут себя, как числа.

Виды матриц:

1. 
   Квадратная матрица – матрица, у которой число строк и столбцов совпадает.
   
2. 
   Нулевая матрица – все элементы равно нулю.
   
3. 
   Вектор-строка – одна строка.
   
4. 
   Вектор-столбец – один столбец.
   
5. 
   Диагональная матрица – матрица, у которой все элементы вне главной диагонали равны нулю.
   
6. 
   Единичная матрица (Е) – диагональная матрица, все ненулевые элементы которой равны 1.
   
7. 
   Верхняя треугольная матрица - все элементы ниже главной диагонали равны нулю.
   
8. 
   Нижняя треугольная матрица – все элементы выше главной диагонали равны нулю.
   

Линейные операции с матрицами:

1. 
   Сумма матриц:
   

Суммой прямоугольных матриц А и В порядка [m*n] называется матрица С, такая что каждый ее элемент является суммой соответствующих элементов матриц А и В.

2. 
   Произведение матрицы А на число b:
   

- матрица С, каждый элемент которой является произведением соответствующего элемента матрицы А на число b.

3. 
   Разница матриц А и В – матрица С = А+(-1)*B
   

Свойства линейных операций:

1) А+В=В+А – переместительное

2) (А+В)+С=А+(В+С) – группировка

3) b*(А+В) = b*А + b*В

4) (a+b)*А = a*A + b*A

5) (a*b)*A = a*(b*A)

6) 1*А=А

7) Существует 0 элемент, такой что 0+А=А. 0 – нулевая матрица

8) Для любой матицы А существует обратная матрица –А: А+(-А)=0

Вопрос 2: Определители n-ого порядка. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки (столбца).

Определителем n-го порядка матрицы А называется число det A, находящееся по формуле:

Det A=

(представлено разложение по первой строке)

Минором матрицы А называется число , которое является определителем (n-1)-го порядка соответствующей матрицы А с вычеркнутой i-строчкой и j-столбцом.

Алгебраическое дополнение:



Теорема о разложении определителя по элементам строки (столбца):

Сумма произведений элементов любой строки (стобца) определителя на их алгебраические дополнения равна этому определителю.

Вопрос 3: Свойства определителей.

СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть

СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,

СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя наь любое число k равносильно умножению определителя на это число k.

СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится.

Вопрос 4: Обратная матрица. Теорема существования и единственности обратной матрицы.

Будем рассматривать множество квадратных матриц n-ого порядка

Матрица В называется левой обратной матрицей к матрице А, если В*А=Е

Матрица С называется правой обратной матрицей к матрице А, если А*С=Е

Теорема единственности: левая и правая обратные матрицы, если они существуют, совпадают:

С=Е*С=(В*А)*С=В*(А*С)=В*Е=В, С=В=А^-1

Теорема существования: для того, чтобы обратная матрица существовала, необходимо и достаточно того, чтобы определитель исходной матрицы был отличен от 0.

Доказательство (2 части):

Необходимость:

Достаточность:

Вопрос 5: Матричные уравнения.

1. 
   АХ=В, A – известное, В – известное, Х – искомая матрица
   

Пусть А^-1 существует, тогда:

А^-1*(А*Х)=А^-1*В

(А^-1*А)*Х=А^-1*В

Е*Х=А^-1*В

Х=А^-1*В

2. 
   XA=B
   

X=B*A^-1

Вопрос 6: Системы линейных уравнений, основные определения. Матричная запись систем линейных уравнений.

Система линейных уравнений – совокупность уравнений, содержащих переменные только в первой степени и не содержащих их произведения.

Имеет общий вид:



Такая система называется системой из n уравнений с n переменными

Числа a_ij называются коэффициентами при переменных, b_i – свободными членами, x_j – неизвестными системы.

Совместная система имеет хотя бы одно решение. Несовместная система решений не имеет.

Система называется определенной, если имеет только одно решение и недоопределенной, если имеет несколько решений.

Систему можно представить в матричном виде: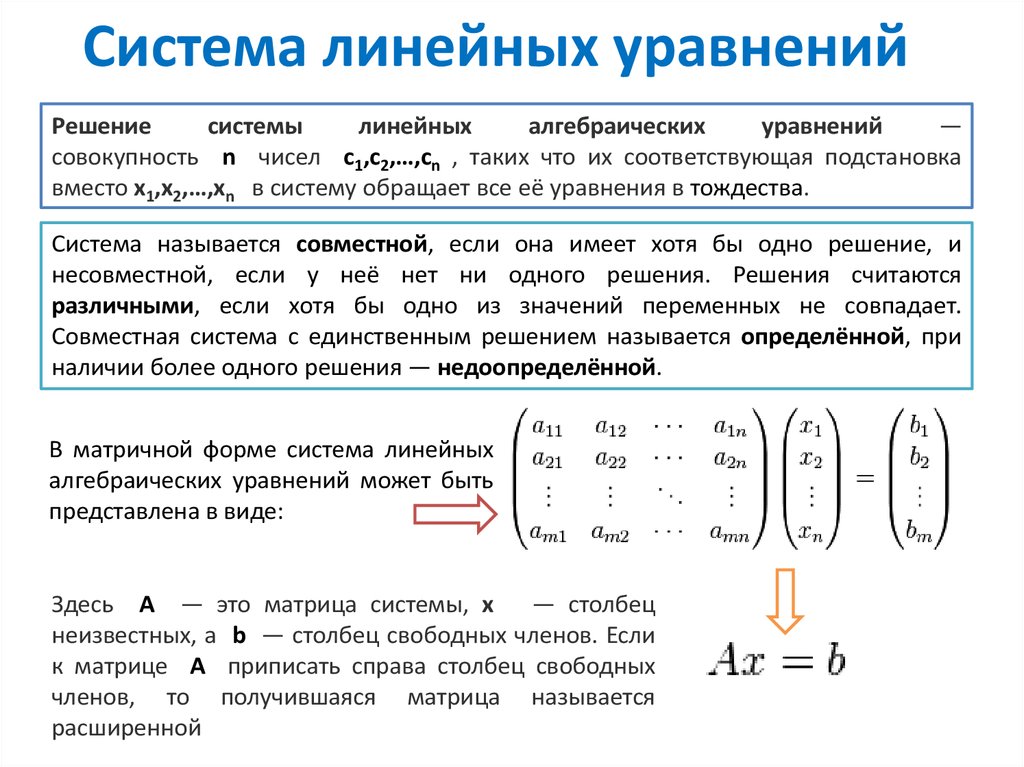



A*X=B

А- матрица системы, Х-столбец неизвестных, B- столбец свободных членов.

Если к матрице А приписать справа В, то такая матрица будет называться расширенной.

Вопрос 7: Решение систем линейных уравнений с помощью обратной матрицы.

Представим систему линейных уравнений

в матричном виде:



A*X=B

Найдем значение матрицы Х, выпишем значения неизвестных.

Вопрос 8: Правило Крамера для систем линейных уравнений.

1. 
   Представим систему линейных уравнений в матричном виде:
   

2. 
   Найдем детерминант матрицы системы detA
   
3. 
   Назовем d_i определитель матрицы, полученной путем подставления столбца свободных членов в матрицу системы на место i-того столбца
   

d₁ = d₂ =…. d₃ =….

4. 
   Найдем значения неизвестных:
   

x₁=d₁/detA

x₂=d₂/detA

…

x_m=d_m/detA

Вопрос 9: Понятие линейного пространства (примеры).

Линенейными или векторными пространствами называются множества М с элементами x,y,z, если выполняется следующее:





Примеры:



Вопрос 10: Линейная зависимость и линейная независимость системы векторов. Свойства.

Элементы x,y,z,… линейного пространства называются линейно зависимыми, если существуют такие числа α, β, γ, …, не все равные 0, что их линейная комбинация с исходными элементами дает 0: αx+βу+γz+…=0

Элементы x,y,z,… линейного пространства называются линейно независимыми, если линейная комбинация αx+βу+γz+…=0 только если α = β = γ =…0.

Теорема:

Для того чтобы элементы x,y,z,… линейного пространства назывались линейно зависимыми, необходимо и достаточно того, чтобы один из элементов являлся линейной комбинацией остальных.

Доказательство:



Следствия:

1. 
   Если среди элементов x,y,z,… есть 0, то эти элементы – линейно зависимые
   
2. 
   Если среди элементов часть линейно зависимы, то и все они линейно зависимы.
   

Вопрос 11: Базис и размерность линейного пространства.

Элементы линейного пространства е₁, е₂, е₃,… называются базисами пространства, если для каждого элемента Х пространства найдутся α₁,α₂,α₃,… , такие что Х– линейная комбинация чисел и базисных векторов: Х= е₁α₁+е₂α₂+е₃α₃+…

Такая запись называется разложением элемента Х по базису е₁, е₂, е₃,…

α₁,α₂,α₃,… - координаты Х в е₁, е₂, е₃,…

Свойства: координаты элемента в базисе определены однозначно;

при сложении элементов в заданном базисе их координаты складываются, при умножении – умножаются.

Линейное пространство М называется n-мерным (dim M=n), если в нем существует n линейно независимых элементов, а каждые n+1 элементов линейно зависимы.

Свойства:

1. 
   Линейное пространство считают бесконечномерным, если в нем существует любое количество линейно независимых элементов.
   
2. 
   Если пространство n-мерно, то каждые n линейно независимых элементов образуют базис.
   
3. 
   Пусть f₁, f₂,f₃,f₄,…f_k - элементы линейного пространства. Пусть g₁,g₂,…,g_l – элементы линейного пространства и являются линейными комбинациями f₁, f₂,f₃,f₄,…f_k. Если g₁,g₂,…,g_l – линейно независимы, то обязательно l⩽k.
   

Вопрос 12: Теорема о разложении вектора по базису, единственность разложения. Координаты вектора в данном базисе.

Каждый элемент пространства раскладывается по базису е₁, е₂, е₃,… единственным образом, то есть координаты α_i элемента определены однозначно.

Доказательство:



α₁,α₂,α₃,…- координаты вектора единственны.

Вопрос 13: Понятие базисного минора. Ранг матрицы.

В матрице порядка [m*n] минор порядка r называется  базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе.

Ранг матрицы:

Опр.1: Ранг матрицы равен наибольшему порядку отличных от нуля миноров.

Опр. 2: Ранг матрицы равен количеству линейно независимых друг от друга строк (стобцов).

Опр. 3: Ранг ступенчатой матрицы равен числу ступеней. Любую матрицу можно привести к ступенчатому виду с помощью элементарных преобразований.

Вопрос 14: Теорема о ранге матрицы.

Основная теорема о ранге матрицы: Базисные строки матрицы линейно независимы. Любая строка матрицы является линейной комбинацией ее базисных строк. Аналогично для столбцов.

Вопрос 15: Методы вычисления ранга матрицы (метод окаймляющих миноров и метод элементарных преобразований).

Метод окаймляющих миноров:

1. 
   Находим не равный нулю минор второго порядка, если такой нашелся, то R ⩾2, если нет, то R=1.
   
2. 
   Найдем неравный нулю минор третьего порядка, элементы которого включают в себя минор второго порядка из прошлого пункта. Если такой нашелся, то R ⩾3, если нет, то R=2.
   
3. 
   Продолжаем аналогично, пока все окаймляющие миноры n-ого порядка не будут равны нулю. Тогда ранг матрицы будет равен n-1.
   

Метод элементарных преобразований:

Так как ранг ступенчатой матрицы равен количеству, ступеней, будем сводить данную матрицу к ступенчатому виду с помощью элементарных преобразований.

Элементарными считаются следующие преобразования:

1. 
   Перестановка строк (столбцов)
   
2. 
   Умножение строки (столбца) на число неравное 0
   
3. 
   Прибавление к строке (столбцу) матрицы линейных комбинаций других строк
   

Теорема: все матрицы, полученные путем элементарных преобразований, являются эквивалентными исходной. Их ранги равны.

Теорема: все матрицы можно привести к ступенчатому виду с помощью элементарных преобразований (кроме 0).

Вопрос 16: Необходимое и достаточное условие равенства нулю определителя n-ого порядка.

Для того, чтобы определитель n-ого порядка был равен нулю, необходимо и достаточно того, чтобы его строки (стобцы) были линейно зависимы.

Вопрос 17: Теорема Кронекера-Капелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Вопрос 18: Решение систем линейных уравнений методом Гаусса.

Приведем систему линейных уравнений к треугольному виду с помощью элементарных преобразований:

1. 
   Пусть a₁₁ неравно 0, разделим первое уравнение на a₁₁. Если a₁₁=0, надо найти уравнение, где a_i1 неравно 0 и подставить на место первого.
   

2. 
   Из каждого последующего уравнения вычесть первое уравнение, умноженное на a_i1.
   
3. 
   Повторять шаги 1 и 2 с уравнениями 2 - n до тех пор, пока система не примет треугольный вид.
   
4. 
   Найти однозначное решение системы или выразить переменные друг через друга, если решение не однозначно.
   

19. 1) Однородные системы уравнений. 2) ФСР. 3) Свойства решений СУ.

1) Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю.свободный член каждого уравнения системы равен нулю.

2) Всякая максимальная линейно независимая система решений однородной системы уравнений (1), называется фундаментальной системой решений (ФСР).

Теорема:

Если ранг r , матрицы из коэффициентов системы линейных однородных уравнений (1), меньше m, то всякая ФСР системы (1) состоит из n-r решений.

3) ????

20. Структура общего решения СЛАУ.

Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения системы.

Пример.

Общее решение системы 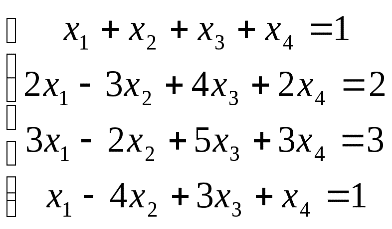 можно записать в виде:

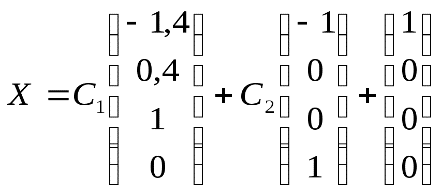, где - частное решение данной системы

21. определение линейного преобразования.





22. Собственные векторы и значения матриц. Характеристический многочлен. Их нахождение.





23. Свойства собственных векторов



24. 1) Квадратичные формы. 2) матрицы кв формы. 3)Канонический и нормальный вид кв формы. 4) Закон инерции.

1) Квадратичной формой f(х₁, х₂,..., х_n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом: f(х₁, х₂,...,х_n) = (a_ij=a_ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическая матрица (т.е. матрица, симметричная относительно главной диагонали, a_ij=a_ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х^ТAX, где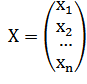

. В самом деле



Например, запишем в матричном виде квадратичную форму  .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому



Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х^TАХ = (CY)^TA(CY) = (Y^TC^T)A(CY) =Y^T(C^TAC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А^*=C^TAC.

Например, найдем квадратичную форму f(y₁, y₂), полученную из квадратичной формыf(х₁, х₂) = 2x₁²+ 4х₁х₂- 3х₂²линейным преобразованием  .

2)

3. 
   Квадратичная форма называется канонической (имеет канонический вид), если все ее коэффициентыa_ij= 0 приi≠j, т.е.f(х₁, х₂,...,х_n) = a₁₁ x₁² + a₂₂ x₂² + … + a_nn x_n² =  .
   

Ее матрица является диагональной.

Теорема(доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Определение. Матрицей квадратичной формы  переменных , называется симметрическая матрица порядка  , элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в  ой строке ом столбце, равен половине коэфициента при  в квадратичной форме.





4) Закон инерции квадратичных форм: число положительных квадратов, как и число отрицательных, в любом каноническом виде данной квадратичной формы одно и тоже и не зависит от того, каким невырожденным линейным преобразованием переменных получен канонический вид. Число положительных квадратов в каноническом виде называют ее положительным индексом инерции и обозначают I₊, число отрицательных квадратов, I_- – отрицательным индексом инерции.

Пример:



здесь p=2, q=1

Эти числа будут постоянными и не будут меняться при изменении линейного преобразования.

25.



26. 1) Положительно и отрицательно определенные кв формы. 2) Критерий Сильвестра.

1) Квадратичная матрица с действительными коэффициентами называется положительно определенной, если  =  и она приводится к нормальному виду, в котором присутствуют только положительные слагаемые:

f= + +…+

Квадратичная матрица с действительными коэффициентами называется отрицательно определенной, если  =  и 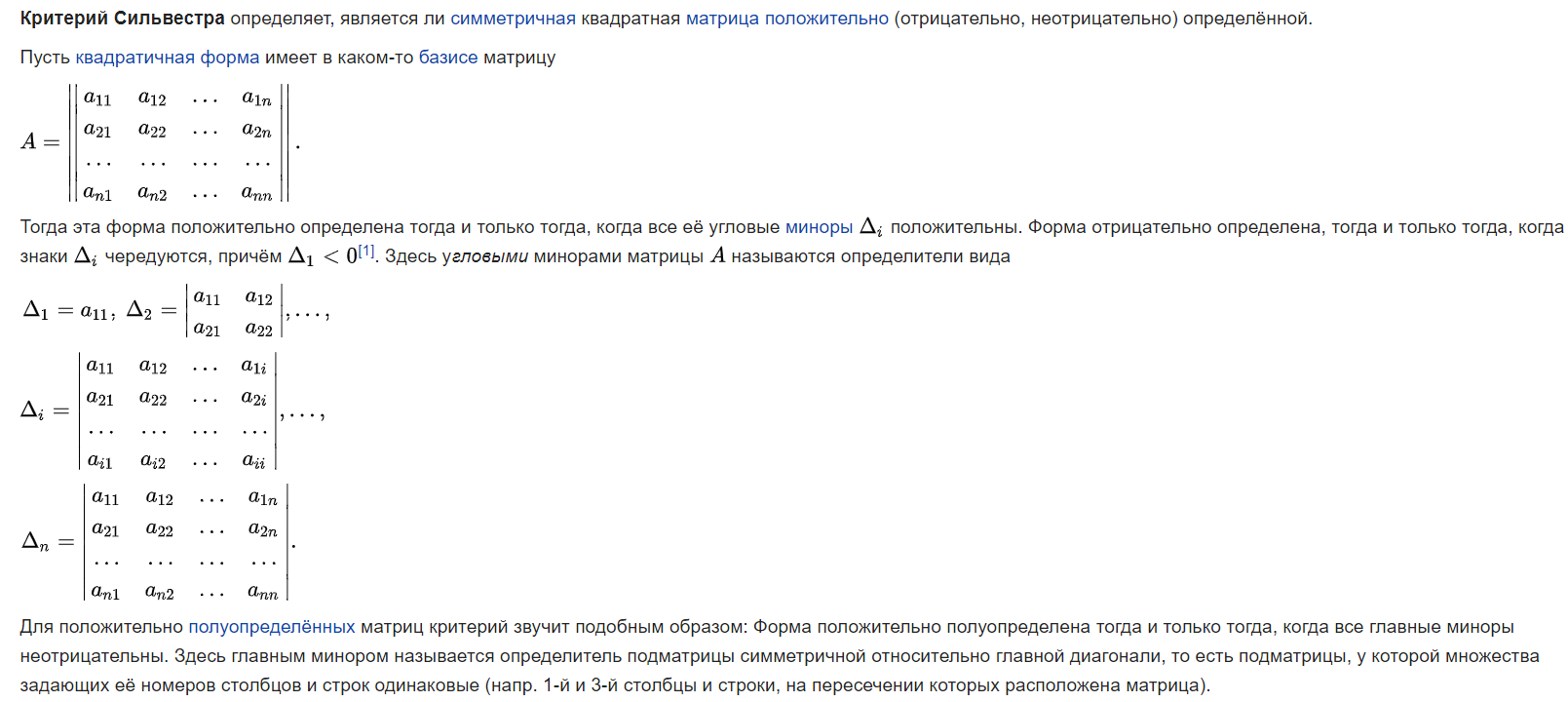она приводится к нормальному виду, в котором присутствуют только отрицательные слагаемые:

• 
  =– – –…– .
  

2)