конспект. Вопросы И ОТВЕТЫ. Вопросы для самостоятельного изучения к экзамену по дисциплине Метрология для заочников Понятие и основные проблемы метрологии Слово метрология

• Название: Вопросы для самостоятельного изучения к экзамену по дисциплине Метрология для заочников Понятие и основные проблемы метрологии Слово метрология
• Анкор: конспект
• Дата: 07.01.2022
• Размер: 0.8 Mb.
• Имя файла: Вопросы И ОТВЕТЫ.doc
• Тип: Документы; #325537
• страница: 9 из 9

Стандартная неопределенность по типу А  u_A оценивается по результатам многократных измерений, причем, исходными данными для ее вычисления являются их результаты 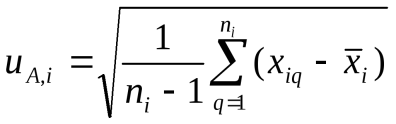 , гдеi = 1,…, m, n_i  число измерений i-ой входной величины. Стандартную неопределенность единичного измерения i-й входной величины u_A,i вычисляют по формуле:

,

где   среднее арифметическое i-й входной величины.

Стандартную неопределенность u_A(x_i) измерений i-й входной величины, при которой результат определяют как среднее арифметическое, вычисляют по формуле: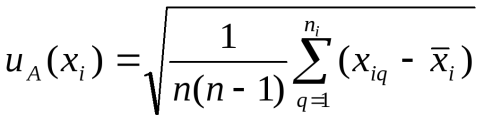

.

Стандартная неопределенность по типу В используется для оценки величины x, которая не была получена в результате повторных наблюдений. Связанная с ней оцененная стандартная неопределенность u_В(x_i) определяется на базе научного суждения, основанного на всей доступной информации о возможной изменчивости х. Фонд такой информации может включать:

- данные предварительных измерений;

- данные, полученные в результате опыта, или общие данные о поведении и свойствах соответствующих материалов и приборов;

- спецификации изготовителя;

- данные о поверке, калибровке, сведения изготовителя о приборе, сертификаты и т.п.;

- неопределенности, приписываемые справочным данным из справочников.

Например, если в свидетельстве о калибровке утверждается, что неопределенность массы эталона равняется 240 мкг на уровне трех стандартных отклонений, то стандартная неопределенность эталона массы равна 240 мкг : 3 = 80 мкг.

Для неопределенности типа В применяется аппарат субъективной теории вероятностей: вероятность характеризует меру доверия, а не частоту событий, как это используется в концепции погрешности, основанной на частотной теории вероятностей. Для определения неопределенности по типу В широко используется априорная информация о неточности используемых данных.

Неопределенность по типу В может быть задана, например, и как некоторое кратное стандартного отклонения, так и как интервал, имеющий 90, 95 или 99 процентный уровень доверия. Если не указано иного, то можно предположить, что использовалось нормальное распределение для вычисления неопределенности. Поэтому стандартную неопределенность можно определить, разделив приведенное значение на соответствующий для нормального распределения коэффициент (см. ниже).

Часто приходится оценивать стандартную неопределенность и(х), связанную с влияющим фактором Х, значения которого находятся в заданных пределах от х -  до х + . По имеющейся информации о величине Х необходимо принять некоторое априор-ное распределение вероятности возможных значений Х внутри заданных пределов. После этого стандартная неопределенность находится делением  на коэффициент k, зависящий от принятой функции распределения: и(х) = /k. Наиболее типичными случаями при этом являются:

1. 
   известны только пределы, в которых, в которых может находиться значение Х, т.е. 2;
   
2. 
   известно значение х_изв и пределы, обычно симметричные, допускаемых значений ;
   
3. 
   известен интервал от (х_изв - _р) до (х_изв + _р), охватывающий заданную долю рвероятности.
   

В первом случае в предположении равномерного распределе-ния значение коэффициента kможет быть принято для симметрич-ных границ равным  .

Во втором случае из-за известного значения х_изв можно предположить, что вероятность нахождения Х вблизи х_изв больше, чем вблизи границ х_изв  . Т.е. можно принять треугольное распре-деление вероятности в качестве некоторого среднего между равно-мерным (прямоугольным) и нормальным. Значение коэффициента k при этом равно  .

В третьем случае распределение вероятности принимается нормальным и значение коэффициента k зависит от заданной вероятности. Например, для р = 0,99 он равен 2,58.

Могут встречаться и другие модификации прямоугольного и нормального распределений, например, в виде равнобедренной трапеции с шириной верхней части, равной 2, где  находится в диапазоне от 1 (прямоугольное распределение) до 0 (треугольное распределение). Тогда значение и(х) определяется исходя из формулы и²(х) = ² (1 + ²)/6.

Правильное использование фонда доступной информации для оценивания стандартной неопределенности по типу В требует интуиции, основанной на опыте и общих знаниях, и является мастерством, которое приходит с практикой.

Оценивание неопределенности по типу В позволяет выйти за рамки традиционного статистического подхода, отнесенного к оцениванию по типу А, и находить значения составляющих неопределенности, для которых получение необходимой статистической информации затруднено или невозможно. К описанию же неопределенностей применяют статистический подход, независимо от способа их оценивания (имея в виду, что все поправки на систематические погрешности уже введены). Это видно на способе определения суммарной стандартной неопределенности.

Суммарная стандартная неопределенность u_c(y) – это стандартная неопределенность результата измерения, когда результат получают из значений ряда других величин. Оцененное стандартное отклонение, связанное с выходной оценкой или с результатом измерения y, называют суммарной стандартной неопределенностью и обозначают u_c(y).

Суммарная стандартная неопределенность для некоррелиро-ванных входных оценок определяется из формулы: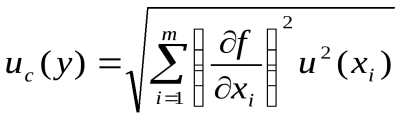



В этой формуле неопределенность u может определяться как по типу А, так и по типу В.

Суммарная стандартная неопределенность представляет собой оцененное стандартное отклонение и характеризует разброс значений, которые могут быть с достаточным основанием приписаны измеряемой величине Y.

Несмотря на то, что суммарная неопределенность может использоваться для выражения неопределенности результата измерения, в некоторых случаях, например, в торговле или при измерениях, касающихся здоровья или безопасности, часто необходимо дать меру неопределенности, которая указывает интервал для результата измерения, в пределах которого находится большая часть распределения значений измеряемой величины. Для этого используется понятие расширенной неопределенности.

Расширенная неопределенность используется для выражения неопределенности результата измерения в торговле, промышленности, регулирующих актах, при охране здоровья и безопасности в качестве дополнительной меры неопределенности. Расширенную неопределенность U получают путем умножения суммарной стандартной неопределенности u_c(y) на коэффициент охвата k:



Тогда результат измерения выражается как Y = y  U. Это означает, что наилучшей оценкой значения, приписываемого величине Y, является у, и что интервал от у - U до у + U содержит, как можно ожидать, большую часть распределения значений, которые можно с достаточной уверенностью приписать Y.

Понятия доверительный интервал и доверительный уровень (вероятность) применяются в статистике к интервалу при условии, что все составляющие неопределенности были бы получены из оценивания по типу А, т.е. при статистической обработке результатов наблюдений. В настоящей концепции слово доверие не используется для модификации слова «интервал» при ссылке на интервал, определяемый U. Термин доверительный уровень также не используется в связи с интервалом и более предпочтительным является термин уровень доверия. U рассматривается как задание интервала вокруг результата измерения, который содержит большую часть рраспределения вероятностей, характеризуемого результатом и его суммарной стандартной неопределенностью. Таким образом, р является вероятностью охвата или уровнем доверия для этого интервала.

При возможности следует оценивать и указывать уровень доверия р, связанный с интервалом U, хотя умножение u_c(y) на постоянную величину не дает никакой новой информации, а представляет уже имевшуюся информацию в новом виде. Но следует признать, что уровень доверия рбудет неопределенным как из-за ограниченного знания распределения вероятностей уи и_с(у), так и из-за неопределенности самой и_с(у).

Значение коэффициента охвата k выбирается на основе уровня доверия, требуемого интервалом от у – U до у – U, и обычно имеет значение от 2 до 3. Но он может и выходить за пределы этого диапазона. На практике связь коэффициента k с заданным уровнем доверия нелегко осуществить из-за отсутствия полного знания распределения вероятностей, характеризуемого результатом измере-ний и суммарной стандартной неопределенностью. Однако, если это распределение вероятностей близко к нормальному, то можно предположить, что принятие k = 2 дает интервал, имеющий уровень доверия около 95 %, а при k = 3  около 99 %. В предположении равномерного распределения коэффициент охвата имеет, соответственно, значения 1,65 и 1,71.

При представлении результата измерения и его неопределенности следует исходить из принципа, что лучше дать слишком много информации, чем слишком мало. Например, следует:

- описать методы, используемые для вычисления результата измерения и его неопределенности из экспериментальных наблюдений и входных данных;

- перечислить все составляющие неопределенности и показать, как они оценивались;

- дать анализ данных таким образом, чтобы можно было легко повторить вычисление представляемого результата;

- дать все поправки и константы, используемые в анализе, и их источники.

Можно рекомендовать следующую процедуру оценивания и выражения неопределенности.

+

1. 
   Выразить математическую зависимость между измеряемой величиной Y и входными величинами X_i, от которых она зависит. Функция fдолжна содержать каждую величину, включая все поправки и поправочные множители, которая может дать значительную составляющую в неопределенность результата измерения.
   
2. 
   Определить х_i  оцененное значение входной величины X_i либо на основе статистического анализа рядов наблюдений, либо другими способами.
   
3. 
   Оценить стандартную неопределенность и(х_i) каждой входной оценки х_iлибо по типу А, либо по типу В.
   
4. 
   Рассчитать результат измерения, т.е. оценку уизмеряемой величины Yиз функциональной зависимости f, используя полученные оценки входных величин х_i.
   
5. 
   Определить суммарную стандартную неопределенность и_с(у) результата измерения у из стандартных неопределенностей, связанных с входными оценками.
   
6. 
   При необходимости дать расширенную неопределенность, следует умножить суммарную стандартную неопределенность и_с(у) на коэффициент охвата k, который обычно находится в диапазоне от 2 до 3. Например, значения коэффициента охвата, который создает интервал, имеющий уровень доверия р при допущении нормального распределения, имеют следующие значения:
   

уровень доверия р, % коэффициент охвата k

68,27 1

90 1,645

95 1,960

95,45 2

99 2,576

99,73 3

42. 
    Международные организации по метрологии
    

Наиболее крупные международные метрологические организации – Международная организация мер и весов (МОМВ) и Международная организация законодательной метрологии (МОЗМ).

Международная организация законодательной метрологии (МОЗМ) учреждена на основе межправительственной Конвенции, подписанной в 1956г. Организация объединяет более 80 государств мира. Цель МОЗМ — разработка общих вопросов законодательной метрологии, в том числе установление классов точности средств измерений; обеспечение единообразия определения типов, образцов и систем измерительных приборов; рекомендации по их испытаниям для унификации метрологических характеристик; порядок поверки и калибровки средств измерений; гармонизация поверочной аппаратуры, методов сличения, поверок и аттестации эталонных, образцовых и рабочих измерительных приборов; выработка оптимальных форм организации метрологических служб и обеспечение единства государственных предписаний по их ведению; оказание научно-технического содействия развивающимся странам в создании и организации работ метрологических служб и их оснащение надлежащим оборудованием; установление единых принципов подготовки кадров в области метрологии с учетом различных уровней квалификации.

Высший руководящий орган МОЗМ — Международная конференция законодательной метрологии, которая созывается с интервалом в четыре года. В работе конференции обычно участвуют не только страны-члены, но и те, которые не планируют стать членами, а также различные международные союзы, чья деятельность связана с метрологией. Решения, принятые МОЗМ, носят рекомендательный характер и лишь морально обязуют страны-члены организации внедрить их по возможности.

Исполнительный орган МОЗМ — Международный комитет законодательной метрологии, состоящий из представителей от каждой страны-члена МОЗМ. При Комитете действует консультативный орган — Совет президента (Международного комитета законодательной метрологии). В состав его входят два вице-президента, директор Международного бюро законодательной метрологии и пять наиболее активных членов Международного комитета законодательной метрологии.

Решения принимаются обычно на сессиях Комитета, которые проводятся ежегодно. Резолюции, принимаемые Комитетом, действительны при единогласной поддержке всех его членов.

+Работу Комитета и Конференции координирует Международное бюро законодательной метрологии (МБМЗ, находится в Париже). Бюро издает информационные материалы, ведет фонд документации, занимается пропагандой достижений в области метрологии.

МОЗМ издает два вида документов: международные документы (МД) и международные рекомендации (МР). МД носят директивный характер и предназначены для рабочих органов МОЗМ, МР — рекомендательный характер и предназначены для стран-членов МОЗМ.

Россию в МОЗМ представляет Госстандарт РФ, а также 12 министерств и ведомств. Участие в МОЗМ дает возможность активно влиять на содержание принимаемых документов, добиваясь их соответствия российским метрологическим стандартам.