конспект. Вопросы И ОТВЕТЫ. Вопросы для самостоятельного изучения к экзамену по дисциплине Метрология для заочников Понятие и основные проблемы метрологии Слово метрология

• Название: Вопросы для самостоятельного изучения к экзамену по дисциплине Метрология для заочников Понятие и основные проблемы метрологии Слово метрология
• Анкор: конспект
• Дата: 07.01.2022
• Размер: 0.8 Mb.
• Имя файла: Вопросы И ОТВЕТЫ.doc
• Тип: Документы; #325537
• страница: 8 из 9

Обработка случайных погрешностей прямых измерений сводится к нахождению   с заданной доверительной вероятностью.

В лабораториях физики МГТУ принят государственный стандарт, в соответствии с которым  = 0,95.

Таблица коэффициентов Стьюдента 

для доверительной вероятности   = 0,95

	12,3	4,3	3,18	2,78	2,6	2,26

 

Полная погрешность измерений   складывается из доверительного интервала и инструментальной погрешности. Теория вероятности дает следующую формулу:

 (5)

Как только найдена полная ошибка, обработка погрешностей закончена. Записываем ответ:

 , (6)

Рядом необходимо указать относительную погрешность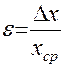

 , (7)

выраженную в процентах ( 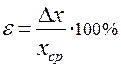  ) (8)

38. 
    Однократные измерения
    

Подавляющее большинство измерений являются од­нократными. Можно сказать, что в обиходе, в торговле, во многих областях производственной деятельности выпол­няются только однократные измерения. В обычных усло­виях их точность вполне приемлема, а простота, высокая производительность (количество измерений в единицу времени) и низкая стоимость (по оценке трудозатрат) ставят их вне конкуренции. Многие люди до конца своей жизни остаются знакомыми только с однократными из­мерениями.

Результат однократного измерения описывается выра­жением (5), приведенным в разд. 2.1. Сам по себе он ни о чем еще не говорит, так как является случайным значени­ем измеряемой величины. Необходимым условием прове­дения однократного измерения служит наличие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и ме­ре его рассеяния, которая извлекается из опыта предшест­вующих измерений. Если ее нет, то используется информа­ция о том, на сколько значение измеряемой величины мо­жет отличаться от результата однократного измерения. Такая информация бывает представлена классом точности средства измерений (см. разд. 4.1). К априорной относит­ся информация о значении аддитивной или мультиплика­тивной поправки (для конкретности ограничимся рассмот­рением аддитивной поправки   ). Если оно не известно, то это учитывается ситуационной моделью, согласно ко­торой с одинаковой вероятностью, например, значение поправки может быть, любым в пределах от   до   . Без априорной информации выполнение однократного измерения бессмысленно.

Порядок действий при однократном измерении пока­зан на рис. 27. Предварительно проводится тщательный анализ априорной информации. В ходе этого анализа уясня­ется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы и меры, направленные на уменьшение их влияния (термостатирование, экранирование, компенсация электрических и маг­нитных полей и др.), значения поправок, принимается решение в пользу той или иной методики измерения, вы­бирается средство измерений, изучаются его метрологи­ческие характеристики и опыт выполнения подобных измерений в прошлом. Важном итогом .этой предваритель­ной работы должна стать твердая уверенность в том, что точности однократного Измерения достаточно для решения поставленной задачи. Если это условие выпол­няется, то после необходимых приготовлений, включаю­щих установку и подготовку к работе средства измере­ний, исключение или компенсацию влияющих факторов, выполняется основная измерительная процедура —получение одного значения отсчета.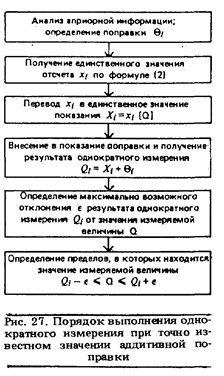


Отсчет, согласно основно­му постулату метрологии, яв­ляется случайным числом. Ни одно из отдельных его зна­чений не дает полного пред­ставления о таком числе. По­этому уже на этапе получе­ния отсчета возникает дефи­цит измерительной информа­ции, который может быть восполнен только за счет ап­риорных сведений.

Единственное значение от­счета   дает одно единствен­ное значение показания   средства измерений, имею­щее ту же размерность, что и измеряемая величина. В это значение показания вносится поправка   . Если ее значе­ние известно точно, то ре­зультат измерения Q будет представлен единственным значением



Если значение поправки не известно, то при выбранной ситуа­ционной модели результат однократного измерения   , с одинаковой вероятностью может быть любым в пределах от   +   до   , +   , ибо в последнем выражении       . Конечной целью измерительного эксперимента является получение достоверной количественной информации о значе­нии измеряемой величины Q. На пути к достижению этой це­липолучение результата однократного измерения служит промежуточным этапом. Дальнейшее зависит от того, какая используется априорная информация. Проанализируем нес­колько конкретных вариантов.

39. 
    Определение результатов косвенных измерений и оценивание их погрешностей
    

Методы обработки результатов косвенных измерений изложены в Методических указаниях РД 50-555-85 «Измерения косвенные. Определение результатов измерений и оценивание их погрешностей».

Основные этапы обработки результатов косвенных измерений следующие.

 1. Искомое значение величины Y находят на основании результатов измерений аргументов x₁, …, x_i, …, x_m, связанных с искомой величиной нелинейной зависимостью . . Вид функции f должен быть известен из теоретических предпосылок или установлен экспериментально. Погрешность неизвестной величины Y зависит от погрешностей измерения аргументов. Ниже рассматривается случай, когда аргументы независимы друг от друга.

2. Оценка СКО случайной погрешности S(Y) вычисляют по формуле:



где x_i– результат измерения а_i-го аргумента; S(x_i) – оценка СКО результата измерения x_i-го аргумента (определяется по формулам раздела 4.6.7).

3. Доверительные границы случайной погрешности e, при условии, что распределение погрешностей результатов измерений аргументов не противоречит нормальному распределению, определяют по формуле: 

4. Границу неисключенной систематической погрешности результата измерения вычисляют по формуле


где k – поправочный коэффициент для принятой доверительной вероятности и числа m составляющих НСП, для Р=0,95 коэффициент k = 1,1.

 5. Погрешность результата измерения вычисляют в зависимости от соотношения границ НСП и случайной погрешности. При   доверительную границу результата косвенного измерения D вычисляют по формуле , где К – коэффициент, зависящий от отношения   и доверительной вероятности (значения К приведены в указанных РД).

6. Результат измерений вычисляется по приведенной выше формуле. Если предполагается исследование и сопоставление результатов измерений или анализ погрешностей, то результат измерения и его погрешность представляют в виде

 .

Если границы погрешности результата измерения симметричны, то результат измерения и его погрешность представляют в виде U ± D.

7. При неизвестных распределениях погрешностей измерений аргументов и при наличии корреляции между ними результат косвенного измерения и его погрешность определяются методом приведения, основанном на приведении ряда отдельных значений косвенно измеряемой величины к ряду прямых измерений. Подробно этот метод описан в упомянутых выше РД.

40. 
    Записи погрешностей и правила округления
    

Для единообразия выражения результатов измерений и погрешностей формы их представления стандартизируются. Основные правила при этом следующие

Так как погрешности определяют лишь зону недостоверности результата измерений, знать их очень точно не требуется. Поэтому в окончательной записи погрешность выражается одной или двумя значащими цифрами. Значащими цифрами числа являются цифры, остающиеся после отбрасывания стоящих впереди нулей. Так, в числах 0,12 и 0,012 находится по две значащие цифры. Принято, что наименьшие разряды числовых значений результата измерений и погрешности должны быть одинаковы: 20,56±0,25 или 2,1±0,1. Одной из самых распространенных ошибок при оценивании результатов и погрешностей измерений является вычисление их с чрезмерно большим числом значащих цифр. Как правило, в этом нет необходимости и только при промежуточных вычислениях можно удерживать по 3-4 значащие цифры.

Лишь при наиболее точных вычислениях оставляют две цифры. Результат измерения должен быть записан так, чтобы он оканчивался десятичным знаком того же разряда, что и значение погрешности. Большее число разрядов не нужно, так как это не уменьшит неопределенности результата, характеризуемого этой погрешностью. Уменьшение же числа разрядов путем округления увеличивает неопределенность результата измерений и уменьшает его точность. Например, погрешность округления погрешности до двух значащих цифр составляет 5 %, а до одной значащей цифры – не более 50 %.

Установлены следующие правила округления результатов и погрешностей измерений:

1. Результат измерения округляется так, чтобы он оканчивался цифрой того же разряда, что и значение его погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то их отбрасывают только до того разряда, который соответствует разряду числового значения погрешности. Например, результат 3, 2800 при погрешности 0,001 округляют до 3,280.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют, лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают. Например, число 267 245 при сохранении четырех значащих цифр должно быть округлено до 267 200; число 165,245 до165,2.

3. Если цифра старшего отбрасываемого разряда больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу: 1459714600; 123,58124;

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или равны нулю, то последнюю сохраняемую цифру не изменяют, если она четная, и увеличивают, если она нечетная: 10,510; 11,512.

41. 
    Основные положения концепции неопределенности
    

В Руководстве вместо понятия «погрешность измерения» вводится понятие «неопределенность измерения». При этом неопределенность измерения трактуется в двух смыслах:

1. 
   В широком смысле как «сомнение» относительно достоверности результата измерения. Например, сомнение в том, насколько точно после внесения всех поправок результат измерения представляет значение измеряемой величины.
   
2. 
   В узком смысле неопределенность измерения понимается как параметр, связанный с результатом измерения, который характеризует разброс значений, которые могли бы быть обоснованно приписаны измеряемой величине.
   

В данной концепции неопределенность измерения понимается именно в узком смысле.

Неопределенность измерения – параметр, связанный с результатом измерения, который характеризует дисперсию (разброс) значений, которые могли бы быть обоснованно приписаны измеряемой величине. Необходимо ясно представлять, что неопределенность измерения – это не доверительный интервал в традиционном понимании (при заданной доверительной вероятности). Вероятность здесь характеризует меру доверия, а не частоту события.

Неопределенность измерения обычно имеет много составляющих. Некоторые из них могут быть оценены из статистического распределения результатов рядов измерений и могут характеризоваться экспериментальными стандартными отклонениями (аналог СКО). Другие составляющие оценивают из предполагаемых распределений вероятностей, основанных на опыте или другой информации. Они также могут характеризоваться стандартными отклонениями.

Неопределенность результата измерения отражает отсутствие точного знания значения измеряемой величины. Оно даже после внесения поправки на известные систематические погрешности все еще является только оценкой измеряемой величины вследствие неопределенности, возникающей из-за случайных эффектов и неточной поправки результата на систематические погрешности.

Водятся две оценки неопределенности:

- оценка по типу А – метод оценивания неопределенности путем статистического анализа рядов наблюдений;

- оценка по типу В – метод оценивания иным способом, чем статистический анализ рядов наблюдений.

Целью классификации на тип А и тип В является показ двух различных способов оценки составляющих неопределенности.

Стандартную неопределенность типа А получают из функции плотности вероятности, полученной из наблюдаемого распределения по частости.

Стандартную неопределенность типа В получают из предполагаемой функции плотности вероятностей, основанной на уверенности в том, что событие произойдет. Эта вероятность часто называется субъективной вероятностью.

В большинстве случаев измеряемая величина Y не является прямо измеряемой, а зависит от m других измеряемых величин X_1, X₂, …, X_m , называемых входными, через функциональную зависимость:



Cами входные величины Х, от которых зависит выходная величина Y, рассматриваются как измеряемые величины. В свою очередь они могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты. Это ведет к сложной функциональной зависимости f, которая, как правило, не может быть записана точно. Кроме того, f можно определить экспериментально или она может существовать как алгоритм, который должен быть реализован численно.

Оценку входной измеряемой величины Y, обозначенную как y, получают из приведенного выше уравнения, используя входные оценки х₁, х₂, …, х_m для значений величин Х₁, Х₂, …, Х_m. Выходная оценка y, которая является результатом измерения, выражается уравнением: