конспект. Вопросы И ОТВЕТЫ. Вопросы для самостоятельного изучения к экзамену по дисциплине Метрология для заочников Понятие и основные проблемы метрологии Слово метрология
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
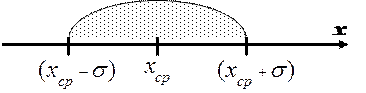
Классификация погрешностей измерений Представленная выше классификация погрешностей измерений связана с причинами их возникновения. Кроме этого существуют и другие признаки, по которым классифицируются погрешности. По характеру проявления (свойствам погрешностей) они разделяются на систематические и случайные, по способам выражения - на абсолютные и относительные. Абсолютная погрешность выражается в единицах измеряемой величины, а относительная погрешность представляет собой отношение абсолютной погрешности к измеренному (действительному) значению величины и ее численное значение выражается либо в процентах, либо в долях единицы. Опыт проведения измерений показывает, что при многократных измерениях одной и той же неизменной физической величины при постоянных условиях погрешность измерений можно представить в виде двух слагаемых, которые по-разному проявляются от измерения к измерению. Существуют факторы, постоянно или закономерно изменяющиеся в процессе проведения измерений и влияющие на результат измерений и его погрешность. Погрешности, вызываемые такими факторами, называются систематическими. Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. В зависимости от характера изменения систематические погрешности подразделяются на постоянные, прогрессирующие, периодические, изменяющиеся по сложному закону. Близость к нулю систематической погрешности отражает правильность измерений. Систематические погрешности обычно оцениваются либо путем теоретического анализа условий измерения, основываясь на известных свойствах средств измерений, либо использованием более точных средств измерений. Как правило, систематические погрешности стараются исключить с помощью поправок. Поправка представляет собой значение величины, вводимое в неисправленный результата измерения с целью исключения систематической погрешности. Знак поправки противоположен знаку величины. На возникновение погрешностей влияют также и факторы, нерегулярно появляющиеся и неожиданно исчезающие. Причем интенсивность их тоже не остается постоянной. Результаты измерения в таких условиях имеют различия, которые индивидуально непредсказуемы, а присущие им закономерности проявляются лишь при значительном числе измерений. Погрешности, появляющиеся в результате действия таких факторов, называются случайными погрешностями. Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью. Незначительность случайных погрешностей говорит о хорошей сходимости измерений, то есть о близости друг к другу результатов измерений, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью. Обнаруживаются случайные погрешности путем повторных измерений одной и той же величины в одних и тех же условиях. Они не могут быть исключены опытным путем, но могут быть оценены при обработке результатов наблюдений. Деление погрешностей измерений на случайные и систематические очень важно, т.к. учет и оценка этих составляющих погрешности требует разных подходов. Факторы, вызывающие погрешности, как правило, можно свести к общему уровню, когда влияние их на формирование погрешности является более или менее одинаковым. Однако некоторые факторы могут проявляться неожиданно сильно, например, резкое падение напряжения в сети. В таком случае могут возникать погрешности, существенно превышающие погрешности, оправданные условиями измерений, свойствами средств измерений и метода измерений, квалификацией оператора. Такие погрешности называются грубыми, или промахами. Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений. Если же причины появления резко выделяющихся наблюдений установить нельзя, то для решения вопроса об их исключении используют статистические методы. Существует несколько критериев, которые позволяют выявить грубые погрешности. Некоторые из них рассмотрены ниже в разделе об обработке результатов измерений. Характеристики оценки измеряемой величины Задачей измерения является нахождение по полученным наблюдениям наилучшей оценки измеряемой величины результата измерения и оценки точности этого результата, т.е. степени его близости к истинному значению величины погрешности измерений. При этом считается, что закон распределения наблюдений и погрешностей известен. Под оценкой в данном случае понимается нахождение значений параметров этих распределений случайных величин по ограниченному числу наблюдений. Полученные оценки параметров распределений являются лишь приближениями к истинным значениям этих параметров и используются в качестве результата измерений и его погрешности. Для того чтобы оценку, получаемую по результатам многократных наблюдений, можно было использовать в качестве параметра функции распределения случайной величины, она должна отвечать ряду требований — быть состоятельной, несмещенной и эффективной. Состоятельная оценка – это оценка, которая при увеличении числа наблюдений стремится к истинному значению оцениваемого параметра. Несмещенная оценка - оценка, математическое ожидание которой равно истинному значению оцениваемого параметра. Эффективная оценка – оценка, имеющая наименьшую дисперсию по сравнению с любой другой оценкой данного параметра. Методы нахождения оценок параметров распределений, а по ним результатов измерений и их погрешностей зависят от вида функции распределения и от тех соглашений по обработке результатов измерений, которые нормируются в рамках законодательной метрологии в нормативной документации. Доверительные интервалы Доверительным называется интервал, который с заданной надежностью Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами –Δх и +Δх составляет Р-ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р×100% всех возможных значений случайной погрешности. Доверительный интервал для нормального распределения находится по формуле: где коэффициент t зависит от доверительной вероятности Р. Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999). Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверительные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф. При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле: где tq – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q-процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P; Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действительного) значения измеряемой величины , оценкой которой является среднее арифметическое Недостатком доверительных интервалов при оценке случайных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погрешностей, т.к. доверительный интервал суммы не равен сумме доверительных интервалов. Суммируются дисперсии независимых случайных величин: Då = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностями. Систематические погрешности Систематическая погрешность средства измерений Систематическая погрешность конкретного средства измерений, как правило, будет отличаться от систематической погрешности другого экземпляра средства измерений этого же типа, вследствие чего для группы однотипных средств измерений систематическая погрешность может иногда рассматриваться как случайная погрешность. Причины возникновения систематических погрешностей и их классификация будут рассмотрены отдельно. Систематические погрешности при измерениях обусловлены разными причинами. Источниками систематических погрешностей могут быть все три компонента измерения: метод измерения, средства измерений и сам экспериментатор. Классификация систематических погрешностей приведена на рис. 1.8. 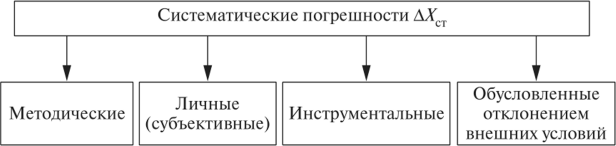 Рис. 1.8. Классификация систематических погрешностей Методы обработки результатов прямых измерений Теперь мы можем приступить к изучению элементарных правил обработки экспериментальных данных. Начнём с самой простой и одновременно важнейшей методики обработки результатов прямых измерений. Обозначим через Поскольку, 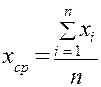 или или 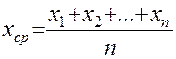 . (1) . (1)Тогда, ошибка отдельного измерения ( Зная ошибку каждого измерения, следующим шагом найдем, так называемоесреднеквадратическое отклонение среднего 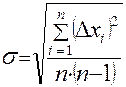 или или 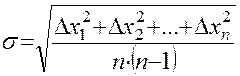 . (3) . (3)(Внимание! Среднеквадратическое отклонение среднего Формула для вычисления
Оказывается, что при проведении новых серий экспериментов, следующие средние значения Вероятность Однако 68% невысокая вероятность. В подавляющем большинстве случаев требуется знать интервал |