ТАУ. Вопросы к экзамену зачету по дисциплине тау
 Скачать 88.32 Kb. Скачать 88.32 Kb.
|
|
Вопросы к экзамену / зачету по дисциплине ТАУ Что является целью управления в системе автоматического регулирования? Ответ: Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами. Какая функция называется передаточной функцией системы? Ответ: Передаточная функция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Какое уравнение называется характеристическим уравнением системы? Ответ: Характеристическое уравнение — алгебраическое уравнение вида определитель в этой формуле получается из определителя матрицы вычитанием величины x из диагональных элементов; он представляет собой многочлен относительно x и называется характеристическим многочленом Вычисление передаточной функции двух звеньев, соединенных последовательно. Ответ: Передаточная функция последовательного соединения звеньев равна произведению передаточных функций отдельных звеньев. Вычисление передаточной функции двух звеньев, соединенных параллельно. Ответ: Передаточная функция группы параллельно соединенных звеньев равна сумме отдельных звеньев. Вычисление передаточной функции двух звеньев, соединенных встречно-параллельно. Ответ: Передаточная функция эквивалентного звена при встречно-параллельном соединении звеньев равна отношению передаточной функции звена прямой цепи к знаменателю, представляющему собой алгебраическую сумму единицы и произведения передаточных функций звена прямой цепи и звена обратной связи. Что такое переходная функция? Ответ: Переходная функция, иногда называют переходный процесс — в теории управления реакция динамической системы на входное воздействие в виде функции Хэвисайда, при заданных начальных условиях. Также реакцию динамической системы на ступенчатое воздействие называют кривой разгона. Временные характеристики звеньев. Ответ: Временные характеристики - динамические свойства звеньев и систем определяются с помощью временных и частотных характеристик. Временные характеристики показывают изменение во времени выходного сигнала исследуемого звена или системы при подаче на их вход типового входного сигнала. Какова взаимосвязь импульсной функции 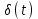 и ступенчатой 1(t)? и ступенчатой 1(t)?Ответ: Единичная ступенчатая функция и единичная импульсная функция связаны соотношением 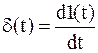 Дельта-функция и ее свойства. Ответ: Дельта-функция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т.) Частотная передаточная функция: определение; ее представление через амплитуду и фазу. Ответ: Частотно передаточная функция представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной. Вещественная и мнимая частотные характеристики; АФЧХ, логарифмические частотные характеристики. Их взаимосвязь. Ответ: Вещественная частотная характеристика U(w) является четной функцией частоты w, а мнимая частотная характеристика V(w) – нечетной. Годограф передаточной функции АФЧХ – график частотной передаточной функции на комплексной плоскости. Логарифмические частотные характеристики (ЛЧХ) - зависимость относительной амплитуды колебаний и фазового сдвига от частоты, построенная в логарифмических или полулогарифмических координатах. Взаимосвязь весовой функции, переходной характеристики и передаточной функции. Ответ: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие. Переходной функцией системы автоматического управления, ее звена, называют функцию, описывающую изменение выходной величины системы (ее звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Импульсную переходную функцию w(t) также называют весовой функцией или функцией веса. Она является выходной координатой элемента или системы при подаче на вход единичного импульса (t). Связь между переходной функцией h(t) и импульсной переходной функцией w(t) выражается соотношением 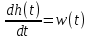 Если частотная передаточная функция задана в виде W(j 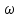 )=U( )=U(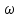 )+jV( )+jV(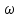 ), то как найти амплитудную частотную характеристику? ), то как найти амплитудную частотную характеристику?Ответ: Как задается звено первого порядка? Ответ: Звено первого порядка обладает двумя параметрами: инерционностью T и коэффициентом усиления k = Y(t = ∞)/X. Чем больше производных учитывается в записи модели, тем со звеном большего порядка мы имеем дело, тем больше коэффициентов при производных следует определить. Передаточная функция звена первого порядка имеет вид: W = k/(Tp + 1),где «p» — символ дифференцирования, тождественно равный «d/dt». Символ «p» также называется алгебраизованным оператором дифференцирования. Как задается звено второго порядка? Ответ: Звеном второго порядка называется звено, связь между выходной и входной величиной которого определяется линейным дифференциальным уравнением второго порядка вида. 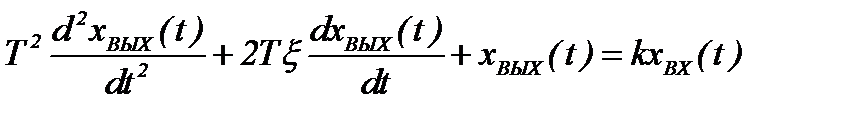 Передаточные функции, временные и частотные характеристики безынерционного звена. Ответ: Безынерционное звено является простейшим среди всех типовых звеньев. Оно передает сигнал со входа на выход мгновенно, без искажений его формы. В звене может происходить только усиление или ослабление мгновенных значений входной величины. Связь между мгновенными значениями входной величины x(t) и выходной величины y(t) описывается алгебраическим уравнением Передаточные свойства звена определяются лишь одним параметром – передаточным коэффициентом k. Передаточные функции, временные и частотные характеристики интегрирующего звена. Ответ: передаточная функция Временные хар-ки Частотные хар-ки Передаточные функции, временные и частотные характеристики дифференцирующего звена. Ответ: передаточная функция Временные хар-ки Частотные хар-ки Передаточные функции, временные и частотные характеристики форсирующего звена первого порядка. Ответ: Передаточную функцию форсирующего звена принято записывать в стандартной форме W (p)=k (1+Tp), где k=k 1 – коэффициент усиления, а T=k 2 /k 1 – постоянная времени звена. Временные хар-ки где Частотные хар-ки Передаточные функции, временные и частотные характеристики апериодического звена первого порядка. Ответ: передаточная функция Временные хар-ки где 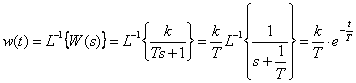 Частотные хар-ки Передаточные функции, временные и частотные характеристики колебательного звена. Ответ: Передаточная функция Временные хар-ки 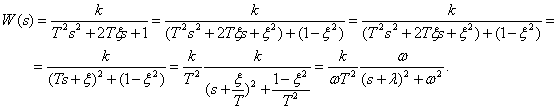 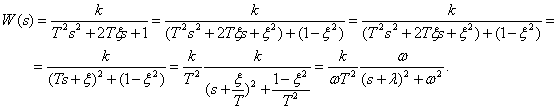 Частотная хар-ка Передаточные функции, временные и частотные характеристики консервативного звена и апериодического звена 2-го порядка. Ответ: передаточная функция 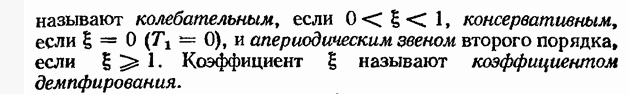 Чему равна фаза для интегрирующего звена. Ответ: Амплитудно-фазовая частотная характеристика интегрирующего звена совпадает с отрицательной мнимой полуосью. Какие значения может принимать коэффициент демпфирования? Ответ: Коэффициент демпфирования - системный параметр, обозначаемый ζ (дзета), который может варьироваться от незатухающий (ζ = 0), недостаточно демпфированный (ζ < 1) через критически затухающий (ζ = 1) к чрезмерно демпфированный (ζ > 1). Где расположены корни характеристического полинома для устойчивой непрерывной САУ? Ответ: Чтобы система была устойчива - необходимо, чтобы все корни характеристического полинома имели отрицательные вещественные части (располагались левее мнимой оси). Если хотя бы один корень характеристического полинома расположен на мнимой оси (а все остальные слева от нее), то такая система находится на границе устойчивости. Необходимый алгебраический критерий устойчивости линейных САУ. Ответ: Необходимым и достаточным условием устойчивости линейной САУ является отрицательность вещественных частей всех корней ее характеристического уравнения. Последнее может быть получено из передаточной функции замкнутой системы, связывающей любые ее вход и выход, путем приравнивания к нулю знаменателя передаточной функции. В соответствии с критерием Гурвица, при выполнении каких условий система будет асимптотически устойчива? Ответ: Если при движении в пространстве точки М и M неограниченно сближаются и разности их координат (yi y' i) 0, то возмущенное движение постепенно возвращается к невозмущенному. Такое движение называется асимптотически устойчивым. Движение называется асимптотически устойчивым, если можно подобрать такое , что, если y0 y0 , то выполняется условие y y 0 при t . 29. В соответствии с критерием Михайлова, где начинается в устойчивой системе годограф Михайлова при  =0? =0?Ответ: Для устойчивых систем годограф Михайлова начинается при 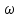 =0 на вещественной полуоси, т.е. D = an, кроме того с ростом частоты фаза должна монотонно возрастать, т.е. вектор должен поворачиваться только против часовой стрелки, так как возрастают фазы элементарных векторов, являющиеся слагаемыми фазы вектора D(i =0 на вещественной полуоси, т.е. D = an, кроме того с ростом частоты фаза должна монотонно возрастать, т.е. вектор должен поворачиваться только против часовой стрелки, так как возрастают фазы элементарных векторов, являющиеся слагаемыми фазы вектора D(i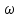 ) )30. Какая точка является критической точкой при определении устойчивости с помощью критерия Найквиста? Ответ: Точка ( 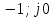 ). ). 31. Какое условие должно выполняться для определения устойчивости замкнутой системы по критерию Найквиста? Ответ: Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении от 0 до 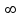 сделал число положительных переходов действительной оси левее точки ( сделал число положительных переходов действительной оси левее точки (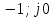 ) больше числа отрицательных переходов на ) больше числа отрицательных переходов на 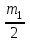 раз. раз.32. Как определяется частота среза 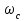 ? ?Ответ: частота среза – это частота, на которой кривая L(w) пересекает ось ω. Критическая частота – частота, на которой фазовая характеристика j (w) равна –180°. 33. Как определяется запас устойчивости по амплитуде и по фазе? Ответ: Запас устойчивости по амплитуде (модулю) определяется величиной допустимого подъема ЛАЧХ, при котором система окажется на границе устойчивости. Запас устойчивости по фазе определяется величиной, на которую должно возрасти запаздывание по фазе в системе с частотой среза , чтобы система оказалась на границе устойчивости. Обычно рассчитывается в градусах. |
