Реферат по экзамену. Вопросы к экзамену по курсу "Методы оптимизации"
 Скачать 38.36 Kb. Скачать 38.36 Kb.
|
|
Вопросы к экзамену по курсу “Методы оптимизации” ( осен.сем. 2017-2018) Классификация задач и методов оптимизации. Привести примеры для каждого критерия и каждого класса. По типу параметров задачи оптимизации. Различают непрерывные задачи оптимизации (continues optimization), дискретные (discrete) и целочисленные (integer optimization). По критерию размерности допустимого множества параметров D. Задачи оптимизации по этому критерию делятся на задачи одномерной и многомерной оптимизации. По критерию наличия или отсутствия ограничений на допустимое множество D. Различают задачи условной (constrained) и безусловной (unconstrained) оптимизации. Этот признак классификации имеет место как для одномерных, так и для многомерных задач оптимизации. По характеру ограничений. Различают детерминированную оптимизацию и стохастическую. Если множество допустимых значений включает случайные компоненты, то имеет место стохастическое программирование. При этом стохастическая оптимизация может относиться и к дискретной задаче. По виду целевой функции и виду ограничений. Различают линейное и нелинейное программирование Бесконечно малая величина (БМВ) и бесконечно большая величина (ББВ). Старший моном БМВ. Построение log-графика для БМВ. Асимптотический способ определения порядка малости коэффициента пропорциональности БМВ. Log-алгоритм определения нецелой кратности корня функции. Порядок точности численных методов. Обобщенные ряды Тейлора. Ряды Пюизё. Раздожение недифференцируемой функции в обобщенный ряд Тейлора. ФНП. Линии уровня. Построение линий уровня для квадратичной формы двух переменных методом выделения полных квадратов. Виды линий уровня. ФНП. Понятие градиента. Взаимосвязь между линиями уровня и градиентами. Геометрические свойства градиента. Гессиан или матрица вторых частных производных. Численные формулы вычисления градиента и гессиана. Абсолютная погрешность формул дифференцирования. Оптимальный шаг дифференцирования. Необходимое условие дифференцирования 1-го порядка. Стационарные точки. Знакоопределенность матрицы. Достаточное условие дифференцирования 2-го порядка. Гессиан. Геометрическая интерпретация матрицы как линейного преобразования пространства. Образ единичной сферы. Связь между образом единичной сферы и единичной линией уровня квадратичной формы. Геометрическая интерпретация числовых характеристик матрицы. Формула Тейлора для функции нескольких переменных. Нахождение точек глобальных экстремумов с помощью условий экстремума. Методы одномерной оптимизации. Критерии останова. Метод деления пополам. Метод золотого сечения. Метод ломаных. Метод Ньютона. Численные методы решения задачи безусловной оптимизации. Липшицевы функции. Выпуклые функции. Критерии выпуклости функций. Метод конфигураций (Хука-Дживса) Метод деформируемого многогранника (Нелдера-Мида). Метод наискорейшего градиентного спуска. Метод сопряженных направлений (Флетчера – Ривса). Метод Ньютона. Задача условной оптимизации. Множество допустимых точек. Активные и неактивные ограничения в допустимой точке. Необходимое условие условной оптимальности первого порядка. Функция Лагранжа для задачи условной оптимизации. Теорема Куна – Таккера (дифференциальная форма необходимого условия минимума). Множители Лагранжа. Условие дополняющей нежесткости. Седловые точки функции Лагранжа. Задача условной оптимизации. Теорема чувствительности оптимального значения. Метод проекции градиента для задачи условной оптимизации. Скорость сходимости. Условия сходимости. Метод условного градиента для задачи условной оптимизации. Скорость сходимости. Условия сходимости. Метод возможных направлений для задачи условной оптимизации. Скорость сходимости. Условия сходимости. Задача линейного программирования(ЛП). Допустимое и оптимальное множество, оптимальное значение. Крайние случаи. Допустимые, разрешимые, неограниченные задачи ЛП. Эквивалентные формы записи задачи ЛП. Каноническая форма. Линии уровня линейной функции. Геометрический способ решения ЗЛП. Неравенства - следствия 1-го и 2-го рода. Лемма Минковского - Фаркаша (формулировка). Двойственная задача ЛП. Теорема о слабой двойственности. Теорема о двойственности (с доказательством). Различные способы построения двойственной задачи ЛП: с помощью леммы Минковского - Фаркаша, с использованием общей схемы построения. Экономическая интерпретация задачи ЛП. Теорема о чувствительности оптимального значения к возмущениям правых частей. Общая формулировка теоремы о чувствительности. Модель оптимизации дохода. Модель оптимизации прибыли. Постановка транспортной задачи, как задачи ЛП. Несбалансированная Т-задача. Метод северо - западного угла нахождения начального решения. Двойственная Т-задача. Проверка оптимальности решения Т-задачи с помощью соотношения двойственности. 15. Метод потенциалов решения Т-задачи. Идея методов отсечения. Понятие правильного отсечения. Метод Гомори решения полностью целочисленной задачи ЛП (с доказательством ). Идея метода ветвей и границ. Метод ветвей и границ для целочисленной задачи ЛП. Идея метода ветвей и границ. Решение задачи о коммивояжере методом ветвей и границ. Задание множества циклов. Вычисление нижних оценок. Разбиение на подмножества. Идея метода ветвей и границ. Решение задачи о коммивояжере методом ветвей и границ. Преобразование матриц расстояний при ветвлении. ЗАДАЧИ Определить порядок малости и константу С погрешности 𝛗(h) правой формулы численного дифференцирования f (x0) ≈ 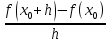 . .В качестве примера возьмите f(x) = sin(x), x0 = 3. Определить порядок малости и константу С погрешности 𝛗(h) центральной формулы численного дифференцирования f (x0) ≈ 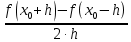 . .В качестве примера возьмите f(x) = sin(x), x0 = 3. Определить порядок малости и константу С погрешности 𝛗(h) центральной формулы численного вычисления второй производной f (x0) ≈ 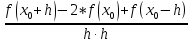 . .В качестве примера возьмите f(x) = sin(x), x0 = 3. Определить порядок малости и константу С абсолютной погрешности 𝛗(h) формулы вычисления определенного интеграла методом трапеций. В качестве примера возьмите f(x) = sin(x), отрезок [1, 3]. Имеется функция нескольких переменных f(x1, …,xn), направление r = (r1, …,rn) единичной длины и фиксированная точка x = (x1, …,xn),. Найти порядок малости α и коэффициент С для функции f в точке x0 по направлению r, то есть для бесконечно малой функции одной переменной g(t) = f(x0 + t·r) - f(x0). Вариант: f(x1, …, xn) = x12 - V·(x1·x2)1/2, r = (1, V), x0 = (1, 1), Постройте линию уровня Uα при α=3 для функции y = x1^2 –V*x1*x2 +2*x2^2 + V*x1. Вычислите и нарисуйте градиент этой функции в точке (1; 1). Найдите гессиан H функции f(x, y) = x^2 +4xy+5y^2 в точке (1; 0). Постройте множество точек, в которое оператор с матрицей H отображает единичную окружность S1 с центром в точке (0; 0). Этот образ является эллипсом. Проверьте, что полуоси являются собственными векторами матрицы H, а длины полуосей – собственными числами i. Проведите квадратичную аппроксимацию в точке (1; 1) для функции F(x, y) = (x - y - 2) e – (x^2 – xy + y^2) Используя критерии оптимальности, найдите экстремумы для функции x^2 -3xy+5y^2+2x-4y +2 Построить график функции и проверить ответ с помощью графика. Найти численным методом точки локальных экстремумов функции одной переменной f(x) = x6 – 2x5 + 4x3 – 10x2 + x. Найти численным методом точку локального минимума функции F(x) = x12 +x22 + x32 +3x1x2 – 2x1x3 – x2x3 + x1 – x2 + x3 на прямой, проходящей через точку x0 = (2, 1, 1) в направлении r = (-1, 2, 1). Улучшить текущее значение функции 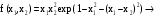 min, min, в точке x0=(-2,-2) методов наискорейшего спуска. Улучшить текущее значение функции min, 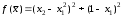 в точке x0=(2, 0) одним из численных методом Ньютона. Улучшить текущее значение функции 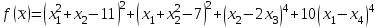 , , методом Ньютона. в точке x0=(2, 0) Методом проекции градиента для задачи условной оптимизации улучшить значение функции 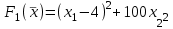 при ограничениях 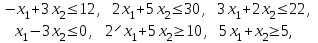 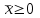 . .Начальную точку выбрать самостоятельно Методом условного градиента для задачи условной оптимизации. 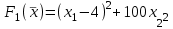 при ограничениях 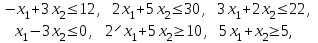 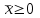 . .Начальную точку выбрать самостоятельно Методом возможных направлений для задачи условной оптимизации. 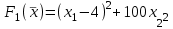 при ограничениях 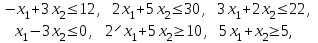  . .Начальную точку выбрать самостоятельно Для изготовления четырёх видов продукции (А, Б, В и Г) используется три вида сырья (I, II и III). Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице:
Определить оптимальный план выпуска продукции из условия максимизации прибыли. | |||||||||||||||||||||||||||||||||||||||
