Шпоргалки по теории информации. Вопросы к зачету по курсу Теория информации

• Название: Вопросы к зачету по курсу Теория информации
• Анкор: Шпоргалки по теории информации.doc
• Дата: 20.02.2018
• Размер: 0.84 Mb.
• Имя файла: Шпоргалки по теории информации.doc
• Тип: Документы; #15744
• Категория: Информатика. Вычислительная техника
• страница: 4 из 6

В соответствии с шенноновским подходом перейдем к информационным характеристикам:

- для последовательностей аргументов поиска определим среднюю энтропию аргументов. Если на аргументы действуют ошибки, то необходимо учесть увеличение средней энтропии вследствие ошибок;

- для множества записей файла определим информационную емкость ключа – максимальное количество информации, которое может содержаться в ключе файла. Если ключи файла могут содержать случайные ошибки, то необходимо учесть уменьшение информационной емкости ключа вследствие ошибок.

Тогда для информационных показателей будет справедлива следующая формулировка теоремы Шеннона для задачи поиска информации:

Для поиска в файле (с помехами и без помех) существует способ сколь угодно достоверного поиска нужных записей, если только средняя энтропия аргумента меньше информационной емкости ключа.

Применение алгоритма идеального кодирования в данной задаче потребует потенциально бесконечного укрупнения файла, чтобы производить поиск в качестве аргумента выступают типичные последовательности исходных аргументов. В этом проявляется техническая нереализуемость идеального кодирования применительно к задаче поиска информации.

Как упоминалось во второй главе, разработка технически реализуемых способов помехоустойчивого поиска в настоящее время находится в зачаточном состоянии своего развития. Имеющиеся здесь результаты существенно скромнее, чем, например, в помехоустойчивом кодировании, где создана обширная и глубокая математическая теория кодирования. В чем здесь дело? Почему бы не воспользоваться результатами теории кодирования для решения родственной задачи поиска.

Основная идея помехоустойчивого кодирования состоит в искусственном введении избыточности в сообщения по подачи их в канал с помехами. В большинстве задач поиска мы имеем дело с естественной избыточностью сообщений, на которую мы не можем активно воздействовать. Мы получаем уже искаженный аргумент поиска, например, невнятно произнесенную по телефону фамилию клиента, и можем рассчитывать только на естественную избыточность языка (естественная избыточность русского языка, как и большинства европейских языков, оставляет примерно 60 % ).Однако, учитывая принципиальную разрешимость этой задачи в свете результатов Шеннона, а также последние публикации по проблемам помехоустойчивого поиска можно надеяться, что эта проблема будет решена и технически.

13. Сжатие данных

Закодированные сообщения передаются по каналам связи, хранятся в запоминающих устройствах, обрабатываются процессором. Объемы данных, циркулирующих в АСУ, велики, и поэтому во многих случаях важно обеспечить такое кодирование данных, которое характеризуется минимальной длиной получающихся сообщений. Эта проблема сжатия данных. Решение её обеспечивает увеличение скорости передачи информации и уменьшение требуемой памяти запоминающих устройств. В конечном итоге это ведет к повышению эффективности системы обработки данных.

Существует два подхода (или два этапа) сжатия данных:

сжатие, основанное на анализе конкретной структуры и смыслового содержания данных;

сжатие, основанное на анализе статистических свойств кодируемых сообщений. В отличие от первого второй подход носит универсальный характер и может использоваться во всех ситуациях, где есть основания полагать, что сообщения подчиняются вероятностным законам. Далее мы рассмотрим оба этих подхода.

Сжатие на основе смыслового содержания данных

Эти методы носят эвристический, уникальный характер, однако основную идею можно пояснить следующим образом. Пусть множество содержит элементов. Тогда для кодирования элементов множества равномерным кодом потребуется двоичных знаков. При этом будут использованы все двоичные кодовые комбинации. Если используются не все комбинации, код будет избыточным. Таким образом, для сокращения избыточности следует попытаться очертить множество возможных значений элементов данных и с учетом этого произвести кодирование. В реальных условиях это не всегда просто, некоторые виды данных имеют очень большую мощность множества возможных значений. Посмотрим, как же поступают в конкретных случаях.

Переход от естественных обозначений к более компактным. Значения многих конкретных данных кодируются в виде, удобном для чтения человеком. При этом они содержат обычно больше символов, чем это необходимо. Например, дата записывается в виде «26 января 1982 г.» или в самой краткой форме: «26.01.82», при этом многие кодовые комбинации, например «33.18.53» или «95.00.11», никогда не используются. Для сжатия таких данных день можно закодировать пятью разрядами, месяц – четырьмя, год – семью, т.е. вся дата займет не более двух байтов. Другой способ записи даты, предложенный еще в средние века состоит в том, чтобы записывать общее число дней, прошедших к настоящему времени с некоторой точки отсчета. При этом часто ограничиваются четырьмя последними цифрами этого представления. Например, 24 мая 1967 года записывается в виде 0000 и отсчет дней от этой даты требует, очевидно, два байта в упакованном десятичном формате.

Аналогичным образом могут быть сжаты номера изделий, уличные адреса и т.п.

Подавление повторяющихся символов. Во многих данных часто присутствуют повторяющиеся подряд символы: в числовых – повторяющиеся старшие или младшие нули, в символьных – пробелы и т.п. Если воспользоваться специальным символом, указывающим на повторение, а после него помещать в закодированном виде число повторений, то тем самым можно уменьшить избыточность, обусловленную повторениями. Например, подавление повторений может быть произведено по следующей схеме. В коде ДКОИ-8 большая часть допустимых кодовых комбинаций не используется. Одну из таких комбинаций (например, с нулем во второй позиции) можно использовать как признак повторения. Тогда байт следующего вида с последующим байтом кода символа заменяют цепочку повторяющихся символов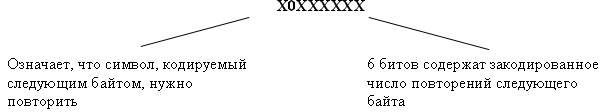


Эффективность такого метода определяется числом и размерами участков повторяющихся символов.

Кодирование часто используемых элементов.Некоторые данные, такие как имена и фамилии, принадлежат множеству возможных значений очень большого размера. Однако в большинстве случаев используется лишь малая часть возможных значений (действует правило «90/10»-в девяноста процентах случаев используется 10 процентов возможных значений). Поэтому для сжатия данных можно определить множество наиболее часто используемых значений, экономно закодировать его элементы и использовать эти коды вместо обычного представления. В частности, имена людей можно кодировать одним байтом, что дает 256 возможных кодовых комбинаций. Если при этом использовать первый разряд как признак пола, то получится 128 женских и 128 мужских имен. Как обеспечить возможность записи имен, не входящих в закодированные? Для этого можно, например, условиться, что некоторая специальная кодовая комбинация длиной в один байт означает, что последующие байты содержат полное написание имени в обычном коде ДКОИ-8.

Аналогичным образом может быть произведено кодирование наиболее употребляемых фамилий (для этого могут понадобиться 2-байтовые коды). Многие сообщения и файлы содержат текстовые фрагменты из некоторых областей знаний. В таких текстах можно выделить множество наиболее употребительных слов, пронумеровать их и закодировать по вышеизложенному способу.

Контекстное сжатие данных. В упорядоченных наборах данных часто совпадают начальные символы или даже группы начальных символов записей. Поэтому можно закодировать данные, рассматривая их в контексте с предыдущими. В этом случае сжимаемым элементом данных может предшествовать специальная кодовая комбинация, характеризующая тип сжатия. Например, возможны комбинации, указывающие на то, что:

элемент данных совпадает с предыдущим;

элемент данных имеет следующее по порядку значение;

элемент совпадает с предыдущим кроме последнего символа;

элемент совпадает с предыдущим кроме двух (трех, четырех и т.д.) последних символов;

элемент длиной lбайтов не имеет связи с предыдущим.

При использовании подобных контекстных символов закодированные данные содержат только отличия текущих элементов от предыдущих.

Реализация сжатия данных требует специальных или (и) программных затрат, а также затрат памяти на предварительное кодирование с целью сжатия данных и последующее декодирование для восстановления первоначальной формы данных. Это означает, что сжатие данных – не всегда целесообразное мероприятие. Например, в базах данных обычно сжимаются архивные файлы с невысокой частотой использования. Сжатие применяется также для сокращения размеров индексных таблиц, используемых для организации поиска информации в индексно-последовательных файлах.


14. Экономное кодирование

Рассмотрим сжатие на основе статистических свойств данных.

Этот подход называется также теорией экономного или эффективного кодирования. Он представляет собой универсальный метод, позволяющий сжимать данные, отвлекаясь от их смысла (семантики). А основываясь только на их статистических свойствах.

Вероятностная модель кодируемых сообщений.

Будем считать, что последовательность, которую нужно закодировать. Составлена из сообщений, принадлежащих некоторому конечному множеству с известным числом элементов N. Появление сообщений в последовательности носит вероятностный характер, т.е. каждому i-му сообщению (I=1,2…N) можно поставить в соответствие вероятность p_i его появления () – условие нормировки. Сообщения кодируются последовательности двоичных знаков (0 и 1). В качестве критерия экономности кода выступает средняя длина кодового слова, необходимая для кодирования одного сообщения.

Экономное кодирование основано на использовании кодов с переменной длиной кодового слова, которые мы и рассмотрим.

Коды с переменной длиной кодового слова.

До сих пор рассматривались равномерные коды, у которых кодовое слово всегда содержит одинаковое число знаков. Однако давно известны и коды, у которых длина кодового слова не постоянна, например код Морзе.

При использовании таких неравномерных кодов возникает задача выделения отдельных кодовых слов из закодированной последовательности для однозначного декодирования сообщений. В коде Морзе для этого предусмотрена специальная кодовая комбинация – разделитель (тройная пауза). Однако более экономным является использование при кодировании так называемого условия префиксности кода (условие Фано): никакое кодовое слово не должно являться началом другого кодового слова. Выполнение этого условия гарантирует однозначное расчленение последовательности на кодовые слова без применения разделителей. Очередное кодовое слово получается последовательным считыванием знаков до тех пор, пока получающаяся комбинация не совпадает с одним из кодовых слов.

Префиксный код называется примитивным, если его нельзя сократить, т.е. при вычеркивании любого знака хотя бы в одном кодовом слове код перестает быть префиксным. Нетрудно видеть, что если код префиксный и мы выбрали любой набор из нулей и единиц, не входящий в число кодовых слов, то возможно одно из двух: либо не существует кодового слова, начальный отрезок которого совпадает с нашим набором, либо (если такое кодовое слово существует), приписав к концу нашего набора нуль или единицу, мы получим какое-то кодовое слово или начальный отрезок кодового слова.

Двоичное кодирование как равномерным, так и неравномерным префиксным кодом удобно представлять в виде бинарного кодового дерева. Если мы всегда условимся сопоставлять левой ветви нуль, а правой – единицу, то каждой свободной вершине дерева будет однозначно соответствовать некоторый набор двоичных знаков, показывающий, в какой последовательности нужно сворачивать направо и налево, добираясь до этой вершины из корня дерева. Таким образом, свободной вершине кодового дерева ставится в соответствие определенное кодовое слово. Например, рассмотренному коду соответствует дерево, приведенное на рис. 3.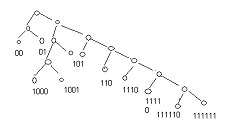



Рис. 3. Кодовое дерево примитивного префиксного кода.

Полезна следующая интерпретация процесса двоичного кодирования. На каждом шаге движения по кодовому дереву от корня к свободным вершинам происходит выбор одного из двух поддеревьев: правого и левого. Это соответствует разбиению множества сообщений на два подмножества (правое и левое) с присвоением им очередных двоичных знаков (единицы и нуля). Так, в рассмотренном примере исходное множество (0, 1,…,9) было разбито на два подмножества (0,1) и (2,3,…,9). При дальнейшем движении вправо множество (2,3,…,9) в свою очередь было разбито на два подмножества (2,3,4) и (5,6,…,9), а при движении влево множество (0,1) было разбито на два подмножества (0) и (1) и т.д. до тех пор, пока во всех подмножествах не осталось по одному элементу. Таким образом, кодовые комбинации характеризуют «историю» последовательного разбиения исходного множества сообщений на правые и левые подмножества.

Минимизация средней длины кодового слова.

Идея использования кодов переменной длины для сжатия данных состоит в том, чтобы сообщениям с большей вероятностью появления ставить в соответствие кодовые комбинации меньшей длины и, наоборот, сообщения с малой вероятностью появления кодировать словами большей длины. Средняя длина кодового слова определяется следующим образом:

,

где li – длина кодового слова для кодирования i-го сообщения

pi - вероятность появления i-го сообщения.

Возникает вопрос, как выбрать кодовые слова, чтобы для заданных вероятностей p1,p2,…..pN обеспечить по возможности меньшую среднюю длину кодового слова?

Для ответа на этот вопрос учтем тот очевидный факт, что равномерный код, всем кодовым комбинациям которого соответствуют равновероятные сообщения, является оптимальным, т.е. имеет минимальную длину кодового слова. На каждом шаге двоичного кодирования производится разбиение множества сообщений на два подмножества, причем одному из них приписывается единица, а другому – ноль. Таким образом, на каждом шаге производится кодирование подмножеств равномерным кодом длиной в I двоичный знак. Отсюда следует принцип: нужно стремиться так производить разбиение на два подмножества, чтобы суммарные вероятности подмножеств были одинаковыми (или как можно более близкими друг к другу).

15. Процедуры Шеннона-Фано и Хаффмена

Процедура Шеннона-Фано.

В этом алгоритме используется следующий способ разбиения на два подмножества на каждом шаге кодирования. Предварительно производится упорядочивание сообщений по убыванию (или возрастанию) вероятностей p_i. Разбиения на множества производится путем выбора разделяющей границы в упорядоченной последовательности так, чтобы суммарные вероятности подмножеств были по возможности одинаковыми. На рис. 4 приведено кодовое дерево, построенное этим методом для рассмотренного выше примера. Для наглядности в вершины дерева записаны подмножества кодируемых сообщений, а возле вершин – суммарные вероятности соответствующих подмножеств.

К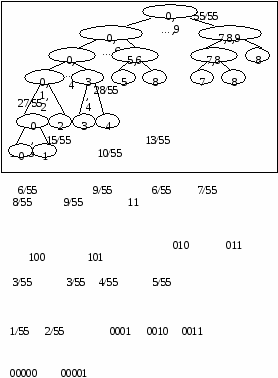одовое дерево, построенное процедурой Шеннона-Фано

Процедура Хафмена.

Процедура Шеннона-Фано является простым алгоритмом построения экономного кода, однако, это не всегда самый лучший из возможных алгоритмов. Причина в том, что мы ограничиваем способ разбиения тем. Что вероятности событий, отнесенных к первому подмножеству, всегда больше (или всегда меньше) вероятностей событий, отнесенных ко второму подмножеству. Оптимальный алгоритм, очевидно, должен учитывать все возможные комбинации событий при разбиении на равновероятные подмножества. Это обеспечивается в процедуре Хафмана экономного кодирования.

Процедура Хаффмана представляет собой рекурсивный алгоритм, стоящий бинарное кодовое дерево в обратную сторону, т.е. от конечных вершин к корню. Конечные вершины представляют отдельные сообщения и их вероятности, корень представляет множество всех сообщений с суммарной вероятностью, равной единице, а внутренние вершины, а внутренние вершины представляют сгруппированные подмножества и их суммарные вероятности. Пусть Pm – задача кодирования сообщений, где сообщение i имеет вероятность появления pi и Основная идея алгоритма состоит в том, чтобы объединить два сообщения с наименьшими вероятностями в одно множество и далее решать задачу Pm-1 c m-1 сообщениями и вероятностями Практически кодовое дерево в явном виде строится в обратном направлении, как показано на рис. 5 для нашего примера.

Кодовое дерево, построенное процедурой Хаффмана.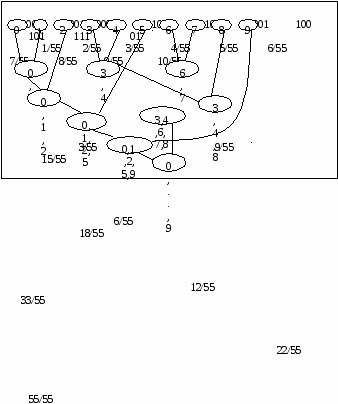



Прямой подсчет дает среднее значение длины кодового слова L=3.145, что совпадает с результатом, полученным с помощью процедуры Шеннона-Фано (это означает, что в данном примере процедура Шеннона-Фано также оказалась оптимальной).

16. Помехоустойчивое кодирование. Основные принципы помехоустойчивого кодирования.

Основные принципы помехоустойчивого кодирования.
Помехоустойчивые коды – одно из наиболее эффективных средств обеспечения высокой верности передачи дискретной информации. Создана специальная теория помехоустойчивого кодирования, быстро развивающаяся в последнее время.
Бурное развитие теории помехоустойчивого кодирования связано с внедрением автоматизированных систем, у которых обработка принимаемой информации осуществляется без участия человека. Использование для обработки информации электронных цифровых вычислительных машин предъявляет очень высокие требования к верности передачи информации.