Шпоргалки по теории информации. Вопросы к зачету по курсу Теория информации
 Скачать 0.84 Mb.
|
|
19. Дискретизация информации. Теорема Котельникова. Классификация сигналов по дискретно-непрерывному признаку. Проблемы дискретизации информации Классификация сигналов по дискретно-непрерывному признаку Все сообщения по характеру изменяющиеся во времени можно разделить на непрерывные и дискретные. Непрерывные по времени сообщения отображаются непрерывной функцией времени. Дискретные по времени сообщения характеризуются тем, что поступают в определенные моменты времени и описываются дискретной функцией t. Сообщения также можно разделить на непрерывные и дискретные по множеству. Непрерывные множеству сообщения характеризуются тем, что функция, их описывающая, может принимать непрерывное множество значений. Дискретные по множеству сообщения – это сообщения, которые могут быть описаны с помощью конечного набора чисел или дискретных значений некоторой функции. Дискретности по множеству и времени не связаны друг с другом. Рассмотрим возможные типы сообщений подробнее. Пусть сигнал описывается функцией X (t) 1) непрерывные по множеству и времени, или просто непрерывные; (рис. 1.2) 2) непрерывные по множеству и дискретные по времени; (рис. 1.3) 3) дискретные по множеству и непрерывные по времени; (рис. 1.4) 4) дискретные по множеству и времени, или просто дискретные; (рис. 1.5)  Проблема дискретизации Согласно строгому определению математического словаря, "дискретность (от лат. discretus – разделенный, прерывистый) – прерывность; противопоставляется непрерывности. Напр., дискретное изменение к.-л. величины во времени – это изменение, происходящее через определенные промежутки времени (скачками); система целых (в противоположность системе действительных чисел) является дискретной". Для большей наглядности дополним данное определение рядом примеров. Дискретными являются показания цифровых измерительных приборов, например, вольтметра (сравните со "старыми", стрелочными приборами). Очевидным (в самом изначальном смысле этого слова!) образом дискретной является распечатка матричного принтера, а линия, проводимая графопостроителем, напротив, является непрерывной. Дискретным является растровый способ представления изображений, тогда как векторная графика по своей сути непрерывна. Дискретна таблица значений функции, но когда мы наносим точки из нее на миллиметровую бумагу и соединяем плавной линией, получается непрерывный график. Механический переключатель диапазонов в приемниках был сконструирован так, чтобы он принимал только фиксированные положения, а вот регулятор громкости вращался плавно, т.е. непрерывно. Какое отношение приведенные выше рассуждения имеют к хранению информации в компьютере? Самое непосредственное! Компьютер по определению способен хранить только дискретную информацию. Его память, как бы велика она не была, состоит из отдельных битов, а значит дискретна. А из этого немедленно следует, что существует проблема преобразования естественной информации в пригодную для компьютера дискретную форму. В литературе ее называют проблемой дискретизации или квантования информации. Н 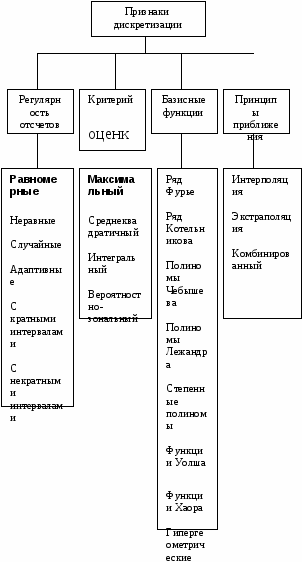 азванная проблема всегда рассматривается при изложении принципов хранения звуковой информации, но обычно умалчивается во всех остальных случаях. Непрерывная величина ассоциируется с графиком функции, а дискретная – с таблицей ее значений. При рассмотрении этих двух объектов разной природы делается вывод о том, что с уменьшением интервала дискретизации (или, что то же самое, с увеличением количества точек в таблице) различия между ними существенно уменьшаются. Последнее означает, что при таких условиях дискретизированная величина хорошо описывает исходную (непрерывную).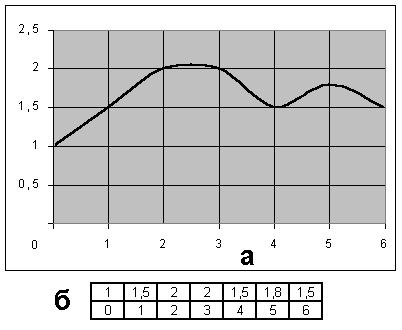 Классификация методов дискретизации. Формулировка теоремы Котельникова: Произвольный сигнал, спектр которого не содержат частот выше Fв, Гц, может быть полностью в осстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени1/(2Fв) с. 20. Квантование по уровню. Дискретизация по времени. Квантование по уровнюсостоит в преобразовании непрерывного множества значений сигнала x(ti) в дискретное множество значений xk, k=0, …., m-1,  .Р 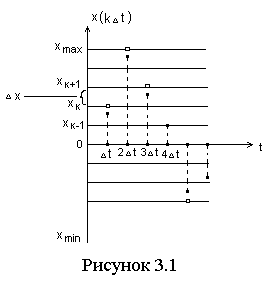 ассмотрим вначале непрерывное сообщение, представляющее собой процесс  с дискретным временем, т.е. совокупность отсчетов непрерывной случайной величины Х. Одна из возможных реализаций такого процесса представлена на рисунке 3.1. Истинные значения сигнала в каждый момент времени показаны точками. Предположим, что все возможные (или по крайней мере наиболее вероятные) значения отсчетов процесса сосредоточены в диапазоне от xmin до xmax. Разобьем весь этот диапазон на конечное число  интервалов  и границы этих интервалов хк-1, хк, хк+1 и т.д. будем считать разрешенными значениями уровней отсчетов процесса. При этом число разрешенных уровней Ny=N-1. Процедура округления истинного значения отсчета до значения ближайшего разрешенного уровня называется квантованием или дискретизацией по значению (уровню) (округленные значения сигнала на рисунке показаны кружочками). Очевидно, что после осуществления операции квантования непрерывная случайная величина Х превращается в дискретную, т.е. имеющую конечное число возможных значений, а непрерывное сообщение - в последовательность элементарных дискретных сообщений источника с объемом алфавита Nу. Из определения операции квантования следует, что ей присуща неизбежная потеря информации, обусловленная наличием погрешности квантования  . Значение этой погрешности (а, следовательно, и количество теряемой из-за нее информации) является контролируемым и может быть сделано необходимо малым путем выбора достаточного количества Nу разрешенных уровней шкалы квантования (вследствие соответствующего уменьшения шага квантования ). Таким образом, непрерывные сообщения, описываемые процессом с дискретным временем, с помощью квантования отсчетов процесса с контролируемой точностью могут быть преобразованы в дискретные.Дискретизация по времени Р 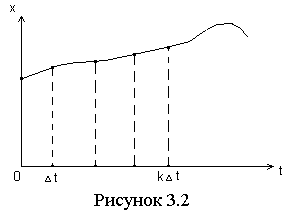 ассмотрим теперь другой тип непрерывных сообщений, описываемый процессами с непрерывным временем. Реализация такого процесса x(t) показана на рисунке 3.2. Очевидно, что если осуществить его дискретизацию , т.е. замену всей совокупности значений процесса отдельными его мгновенными значениями, выбранными в определенные "разрешенные" моменты времени  , то он превращается в уже рассмотренный процесс с дискретным временем X¶(t). На первый взгляд дискретизация приводит к необратимым существенным потерям информации, обусловленным <отбрасыванием> большей части мгновенных значений процесса. Однако, как будет видно из дальнейших рассуждений, дело обстоит не совсем так (почти совсем ни так).Ввиду особой важности процедуры дискретизации для процессов передачи и преобразования непрерывных сообщений рассмотрим ее более подробно. П 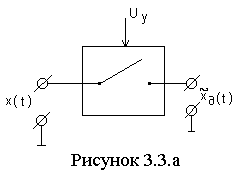 рактическая реализация процесса дискретизации может быть осуществлена с помощью упрощенной схемы, показанной на рисунке 3.3.а. Электронный ключ управляется последовательностью коротких, но имеющих конечную длительность t, импульсов uу(t), следующих с периодом Dt, равным шагу дискретизации, т.е. интервалу времени между соседними выбираемыми в процессе дискретизации значениями сигнала. На время действия импульса ключ замыкается, и выход схемы оказывается подключенным к входу. Дискретизация по времени состоит в преобразовании сигнала x(t), непрерывного аргумента t в сигнал x(ti) дискретного аргумента ti. |