Шпоргалки по теории информации. Вопросы к зачету по курсу Теория информации
 Скачать 0.84 Mb.
|
При одновременном наблюдении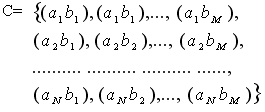  Мера Хартли:   Доказательство аддитивности информационной меры Шеннона. Пусть А и В независимы, тогда 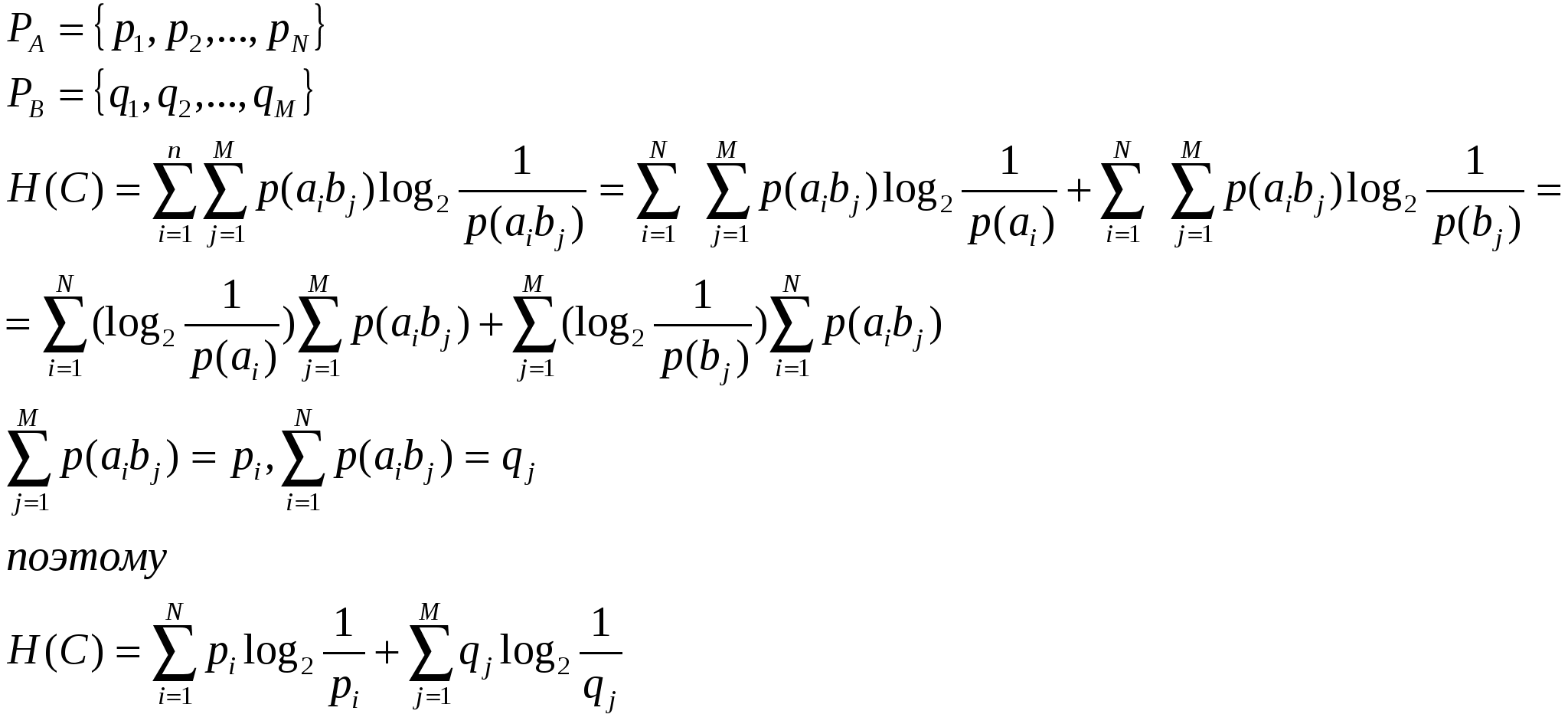  Энтропия непрерывных сообщений Непрерывные системы передачи информации - системы, в которых как реализации сообщения, так и реализации сигнала на конечном временном интервале  представляют собой некоторые непрерывные функции времени.Пусть  - реализации непрерывного сообщения на входе какого-либо блока схемы связи,  - реализация выходного сообщения (сигнала),  - плотность вероятности ансамбля входных сообщений,  - плотность вероятности ансамбля выходных сообщенийФормулы для энтропии  непрерывных сообщений получаются путем обобщения формул для энтропии дискретных сообщений. Если  - интервал квантования (точность измерения), то при достаточно малом энтропия непрерывных сообщений где  По аналогии  8. Избыточность информации. Взаимная информация. Избыточность информации Сообщения, энтропия которых максимальна, являются оптимальными с точки зрения символьного количества представляемой информации. Мерой количественной оценки того, насколько данное реальное сообщение по своей энтропии отличается от соответствующего ему оптимального сообщения, является коэффициент сжатия.  ;где Н(ξ) – энтропия реального сообщения, max H(ξ) – энтропия соответствующего ему оптимального сообщения. Если оптимальное и неоптимальное сообщение характеризуются одинаково общей энтропией, то n*H(ξ) = n’*max H(ξ), где n – число элементов неоптимального сообщения, n’ – число элементов оптимального сообщения. Так как средняя на элемент оптимальная энтропия максимальна, то число элементов неоптимального сообщения больше числа элементов соответственного ему оптимального сообщения.   ;таким образом реальные сообщения при одинаковой информативности обладают определенной избыточностью в элементах по сравнению с оптимальными сообщениями. Мерой количественной оценки избыточности является коэффициент избыточности.  ; смысл: это относительный избыток символов при передачи информации данным источником, которая потребуется по сравнению со случаем использования безызбыточного алфавита. Безызбыточный алфавит (ρ=0) характеризуется равными вероятностями появления символов. Избыточность приводит к повышению времени передачи сообщений, излишней загрузке канала связи. Однако, некоторая избыточность бывает полезной для обеспечения требуемой надежности систем, появления помехоустойчивости передачи сообщений. Взаимной информацией величин  и  называется  Справедливы следующие соотношения:       Если и независимы, то  =0.При расчетах условной энтропии и взаимной информации удобно пользоваться следующими соотношениями теории вероятностей: 1) теорема умножения вероятностей  ;2) формула полной вероятности   3) формула Байеса 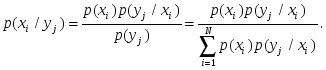 Свойства взаимной информации. Анализируя соотношение для взаимной информации можно установить следующие ее свойства (предлагаем провести доказательство самостоятельно):
3)  ,причем равенство имеет место тогда и только тогда, когда £ и п взаимно однозначны.9. Обобщенные характеристики сигналов и каналов Сигнал может быть охарактеризован различными параметрами. Таких параметров, вообще говоря, очень много, но для задач, которые приходится решать на практике, существенно лишь небольшое их число. Например, при выборе прибора для контроля технологического процесса может потребоваться знание дисперсии сигнала; если сигнал используется для управления, существенным является его мощность и так далее. Рассматривают три основных параметра сигнала, существенных для передачи информации по каналу. Первый важный параметр - это время передачи сигнала Tс. Второй характеристикой, которую приходится учитывать, является мощность Pс сигнала, передаваемого по каналу с определенным уровнем помех Pz . Чем больше значение Pс по сравнению с Pz, тем меньше вероятность ошибочного приема. Таким образом, представляет интерес отношение Pс /Pz. Удобно пользоваться логарифмом этого отношения, называемым превышением сигнала над помехой:  Третьим важным параметром является спектр частот Fc. Эти три параметра позволяют представить любой сигнал в трехмерном пространстве с координатами L, T, F в виде параллелепипеда с объемом TcFcLc. Это произведение носит название объема сигнала и обозначается через Vc Информационный канал можно характеризовать также тремя соответствующими параметрами: временем использования канала Тк , шириной полосы частот, пропускаемых каналом Fk, и динамическим диапазоном канала Dk характеризующим его способность передавать различные уровни сигнала.Величина  называется емкостью канала.Неискаженная передача сигналов возможна только при условии, что сигнал по своему объему «вмещается» в емкость канала. Следовательно, общее условие согласования сигнала с каналом передачи информации определяется соотношением  Однако соотношение выражает необходимое, но недостаточное условие согласования сигнала с каналом. Достаточным условием является согласование по всем параметрам: 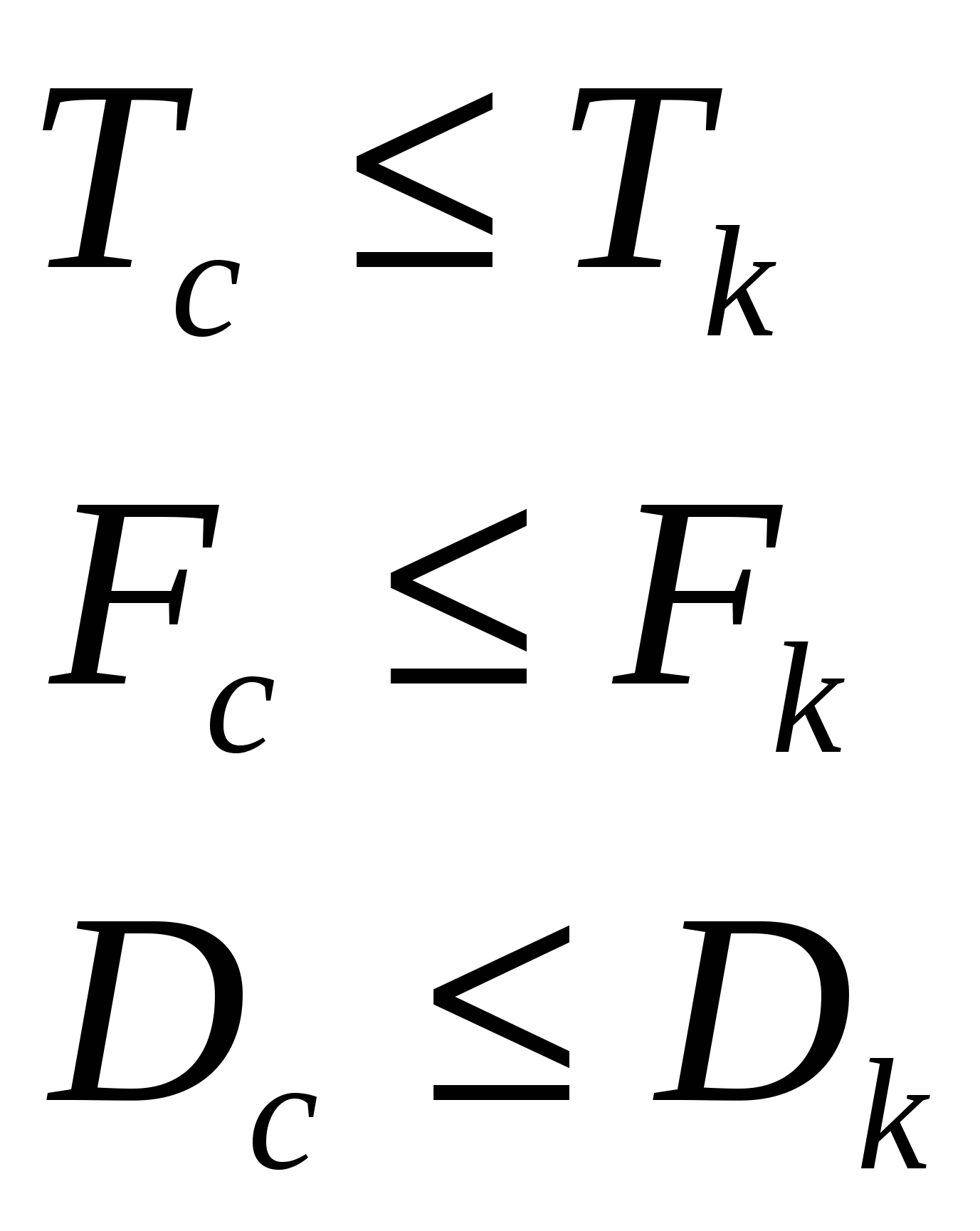 Для информационного канала пользуются понятиями: скорость ввода информации, скорость передачи информации и пропускная способность канала. Под скоростью ввода информации (потоком информации) V(A) понимают среднее количество информации, вводимое от источника сообщений в информационный канал в единицу времени. Эта характеристика источника сообщений и определяется только статистическими свойствами сообщений. Скорость передачи информации V(X,Y) – среднее количество информации, передаваемое по каналу в единицу времени. Она зависит от статистических свойств передаваемого сигнала и от свойств канала. Пропускная способность С – наибольшая теоретически достижимая для данного канала скорость передачи информации. Это характеристика канала и не зависит от статистики сигнала. С целью наиболее эффективного использования информационного канала необходимо принимать меры к тому, чтобы скорость передачи информации была как можно ближе к пропускной способности канала. Вместе с тем скорость ввода информации не должна превышать пропускную способность канала, иначе не вся информация будет передана по каналу. Это основное условие динамического согласования источника сообщений и информационного канала. Одним из основных вопросов в теории передачи информации является определение зависимости скорости передачи информации и пропускной способности от параметров канала и характеристик сигналов и помех. Эти вопросы были впервые глубоко исследованы К. Шенноном. 10. Характеристика канала связи без помех. Теорема Шеннона для канала без помех. Дискретный канал передачи информации – совокупность средств, предназначенных для передачи дискретных сигналов. В канале без помех каждому определенному входному сигналу будет соответствовать один и тот же сигнал на выходе канала, то есть входные и выходные сигналы связаны однозначной функциональной зависимостью.  Выходной алфавит символов источника сообщений:  Количество информации, приходящееся в среднем на один символ источника:  , где pi – вероятность появления символа ai на выходе источника.Алфавит символов канала связи:  Среднее количество информации, выдаваемое источником в единицу времени – информационная производительность:  где  - среднее число символов, выдаваемое источником в единицу времени.Скорость передачи информации по каналу:  где  -среднее число символов, передаваемое по каналу в единицу времени.Пропускная способность канала:  множество всех возможных распределений вероятностей символов алфавита B канала.Пропускная способность канала (с учетом свойств энтропии):   - технические характеристики канала связи.Теорема Шеннона для канала без помех Рассмотрим две фундаментальные теоремы идеального кодирования, носящие имя Шеннона. Первая из них рассматривает случай отсутствия помех в канале, вторая учитывает наличие помех, приводящих к ошибкам. Рассмотрим проблему согласования источника сообщений и канала при передаче последовательности сообщений. Пусть источник сообщений выдает сообщения с некоторой скоростью  (сообщений/ед. времени), называемой технической производительностью источника. Пусть по каналу можно передавать без искажений сообщения со скоростью, не превышающей некоторую величину (сообщений/ед. времени), называемую технической пропускной способностью канала. Очевидно, что если выполняется условие <, то канал успевает передать все сообщения, поступающие на его вход от источника, и передача будет вестись без искажений. Что произойдет, если  > ? Можно ли в этом случае обеспечить передачу без искажений? Если исходить только из технических характеристик, то, очевидно, нельзя. А если учесть информационные характеристики? Ведь нам известно, что если последовательность обладает информационной избыточностью, то её можно сжать, применив методы экономного кодирования. Рассмотрим подробнее такую возможность.Пусть Vu - (информационная) производительность источника, т.е. количество информации, производимое источником в единицу времени; Ck – (информационная) пропускная способность канала, т.е. максимальное количество информации, которое способен передать канал без искажений за единицу времени. Первая теорема Шеннона утверждает, что безошибочная передача сообщений определяется соотношением Vu и Ck. Первая теорема Шеннона: если пропускная способность канала без помех превышает производительность источника сообщений, т.е. удовлетворяется условие Ck >Vu, то существует способ кодирования и декодирования сообщений источника, обеспечивающий сколь угодно высокую надежность передачи сообщений. В противном случае, т.е. если Ck Такого способа нет. Таким образом, идеальное кодирование по Шеннону по существу представляет собой экономное кодирование последовательности сообщений при безграничном укрупнении сообщений. Такой способ кодирования характеризуется задержкой сообщений  поскольку кодирование очередной типичной последовательности может начаться только после получения последовательности источника длительностью T, а декодирование – только когда принята последовательность из канала той же длительности T. Поскольку требуется  , то идеальное кодирование требует бесконечной задержки передачи информации. В этом причина технической нереализуемости идеального кодирования по Шеннону. Тем не менее, значение этого результата, устанавливающего предельные соотношения информационных характеристик источника и канала для безошибочной передачи сообщений, весьма велико. Исторически именно теорема Шеннона инициировала и определила развитие практических методов экономного кодирования.11. Характеристика канала связи с помехами. Теорема Шеннона для канала с помехами.  |
, т.е. наблюдая 7], мы получим о £ такое
, причем равенство имеет место тогда и только тогда, когда £ и rjстатистически независимы;