Шпоргалки по теории информации. Вопросы к зачету по курсу Теория информации

• Название: Вопросы к зачету по курсу Теория информации
• Анкор: Шпоргалки по теории информации.doc
• Дата: 20.02.2018
• Размер: 0.84 Mb.
• Имя файла: Шпоргалки по теории информации.doc
• Тип: Документы; #15744
• Категория: Информатика. Вычислительная техника
• страница: 5 из 6

Теорема Шеннона для дискретного канала с помехами утверждает, что вероятность ошибок за счет действия в канале помех может быть обеспечена сколь угодно малой путем выбора соответствующего способа кодирования сигналов. Из этой теоремы вытекает весьма важный вывод о том, что наличие помех не накладывает принципиально ограничений на верность передачи.

Однако в теореме Шеннона не говорится о том, как нужно строить помехоустойчивые коды.

На этот вопрос отвечает теория помехоустойчивого кодирования.

Рассмотрим сущность помехоустойчивого кодирования, а также некоторые теоремы и определения, относящиеся к теории такого кодирования.

Под помехоустойчивыми или корректирующими кодами понимают коды, позволяющие обнаружить и устранить ошибки, происходящие при передаче из-за влияния помех.

Для выяснения идеи помехоустойчивого кодирования рассмотрим двоичный код, нашедший на практике наиболее широкое применение.

Напомним, что двоичный код – это код с основание m=2.

Количество разрядов n в кодовой комбинации принято называть длиной или значностью кода. Каждый разряд может принимать значение 0 или 1. Количество единиц в кодовой комбинации называют весом кодовой комбинации и обозначают .

Ошибки, вследствие воздействия помех, появляются в том, что в одном или нескольких разрядах кодовой комбинации нули переходят в единицы и, наоборот, единицы переходят в нули. В результате создается новая ложная кодовая комбинация.

Если ошибки происходят только в одном разряде кодовой комбинации, то такие ошибки называются однократными. При наличии ошибок в двух, трех и т.д. разрядах ошибки называются двукратными, трехкратными и т.д.

Для указания мест в кодовой комбинации, где имеются искажения символов, используется вектор ошибки . Вектор ошибки n-разрядного кода – это n-разрядная комбинация, единицы в которой указывают положение искаженных символов кодовой комбинации. Например, если для пятиразрядного кода вектор ошибки имеет =01100, то это значит, что имеют место ошибки в третьем и четвертом разрядах кодовой комбинации.

Вес вектора ошибки характеризует кратность ошибки. Сумма по модулю для искажений кодовой комбинации и вектора ошибки дает исходную неискаженную комбинацию.

Помехоустойчивость кодирования обеспечивается за счет введения избыточности в кодовые комбинации. Это значит, что из n символов кодовой комбинации для передачи информации используется k<n символов. Следовательно, из общего числа возможных кодовых комбинаций для передачи информации используется только комбинаций. В соответствии с этим все множества возможных кодовых комбинаций делятся на две группы. В первую группу входит множество разрешенных комбинаций. Вторая группа включает в себя множество запрещенных комбинаций.

Если на приемной стороне установлено, что принятая комбинация относится к группе разрешенных, то считается, что сигнал пришел без искажений. В противном случае делается вывод, что принятая комбинация искажена. Однако это справедливо лишь для таких помех, когда исключена возможность перехода одних разрешенных комбинаций в другие.

В общем случае каждая из N разрешенных комбинаций может трансформироваться в любую из N₀ возможных комбинаций, т.е. всего имеется N*N₀ возможных случаев передачи (рис.1), из них N случаев безошибочной передачи (на рис. 1 обозначены жирными линиями), N(N-1) случаев перехода в другие разрешенные комбинации (на рис. 1 обозначены пунктирными линиями) и N(N₀- N) случаев перехода в запрещенные комбинации (на рис. 7.3 обозначены штрих пунктирными линиями).

Таким образом, не все искажения могут быть обнаружены. Доля обнаруживаемых ошибочных комбинаций составляет



Для использования данного кода в качестве исправляющего множество запрещенных кодовых комбинаций разбивается на Nнепересекающихся подмножеств M_k. Каждое из множеств M_kставится в соответствие одной из разрешенных комбинаций.

Если принятая запрещенная комбинация принадлежит подмножеству M_i , то считается, что передана комбинация A_i

Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из комбинации A_i. Таким образом, ошибка исправляется в случаях, равных количеству запрещенных комбинаций. Доля исправляемых ошибочных комбинаций от общего числа обнаруживаемых ошибочных комбинаций составляет


Способ разбиения на подмножества зависит от того, какие ошибки должны исправляться данным кодом.

Связь исправляющей способности кода с кодовым расстоянием.

Для оценки степени различия между двумя произвольными комбинациями данного кода используется характеристика, получившая название расстояния между кодовыми комбинациями. Наименьшее расстояние между разрешенными кодовыми комбинациями называют кодовым расстоянием и обозначают d_min . Это очень важная характеристика кода, ибо именно она характеризует его корректирующие способности.

Рассмотрим это на конкретных примерах.

Пусть необходимо построить код, обнаруживающий все ошибки кратностью t и ниже.

Построить такой код – это значит, из множества N₀ возможных комбинаций выбрать Nразрешенных комбинаций так, чтобы любая из них в сумме по модулю два с любым вектором ошибок с весом не дала бы в результате никакой другой разрешенной комбинации. Для этого необходимо, чтобы кодовое расстояние удовлетворяло условию

7.29

В общем случае для устранения ошибок кратности кодовое расстояние должно удовлетворять условию

7.31

Аналогично рассуждая, можно установить, что для исправления всех ошибок кратности не более и одновременного обнаружения всех ошибок кратности не более t (при t>) кодовое расстояние должно удовлетворять условию

7.32

При этом нужно иметь в виду, что если обнаруженная кодом ошибка исправлена быть не может, т.е. в данном случае код только обнаруживает ошибку.
17. Помехоустойчивое кодирование. Помехоустойчивость кода. Корректирующие коды.

Помехоустойчивость кода.

Минимальное кодовое расстояние некоторого кода определяется как минимальное расстояние Хэмминга между любыми разрешенными кодовыми словами этого кода. У безызбыточного кода минимальное кодовое расстояние d_min=1. Чем больше минимальное кодовое расстояние, тем больше избыточность кода. Максимальное кодовое расстояние кода, очевидно, равно его размеру, т.е. числу двоичных разрядов в кодовом слове.

Непосредственные вычисления кодовых расстояний у рассмотренного выше кода, построенного методом контрольных сумм, дают следующие значения показателей: d_min=3 и d_max=7.

Очевидно, что -кратная ошибка приводит к тому, что искаженная кодовая комбинация отодвигается от исходной на расстояние . В то же время ошибка не может быть обнаружена, если она переводит одну разрешенную кодовую комбинацию в другую, тоже разрешенную. Следовательно, способность кода обнаруживать все ошибки некоторой кратности зависит от минимального расстояния между разрешенными кодовыми словами: чем больше минимальное кодовое расстояние, тем большей кратности требуется ошибка для перевода любой разрешенной кодовой комбинации в другую разрешенную. Таким образом, можно утверждать, что код с минимальным кодовым расстоянием d_minспособен обнаруживать любые ошибки кратностью

У рассмотренного выше кода d_min=3, следовательно, он может обнаруживать любые однократные и двукратные ошибки.

Способность кода исправлять обнаруженные ошибки состоит в возможности однозначного отнесения запрещенной кодовой комбинации к единственной разрешенной. Для этого необходимо, чтобы минимальное кодовое расстояние превышало расстояние, порождаемое действием двух любых ошибок. Действительно, в этом случае запрещенные кодовые комбинации, получающиеся в результате ошибок из одного кодового слова, никогда не совпадут с запрещенными комбинациями, получающимися в результате ошибок из любого другого кодового слова, а тем более – с другими разрешенными кодовыми словами. Таким образом, необходимо, чтобы выполнялось условие откуда следует

У рассмотренного выше кода, построенного методом контрольных сумм, d_min=3, следовательно, он может исправлять только любые однократные ошибки.

Рассмотрим n-разрядный код, основанный на n-кратном повторении каждого передаваемого символа. У него d_min= n. Следовательно, максимальная кратность обнаруживаемых ошибок равна, что соответствует случаю искажения всех символов, кроме одного. Максимальная кратность исправляемых ошибок равна (n-1)/2, что соответствует искажению «почти» половины всех символов. Это соответствует фиксации ошибки при обнаружении хотя бы одного неодинакового символа и исправлению ошибки на основе определения, каких значений больше.

Рассмотрим n-разрядный код, основанный на введении одного разряда контроля четности. У него d_min= 2, и, следовательно, максимальеная кратность обнаруживаемых ошибок равна 1, а исправляемых – 0 (код не способен исправлять ошибки).

Граница Хэмминга. Рассмотрим задачу немного иначе. Возьмём n-разрядный код и зададимся вопросом о том, сколько контрольных разрядов должно быть в каждом кодовом слове, чтобы код мог исправлять все ошибки заданной максимальной кратности (разумеется, ).

Возьмём какое-либо разрешенное кодовое слово и подсчитаем общее число кодовых комбинаций, порождаемых из него всевозможными ошибками кратностью не выше 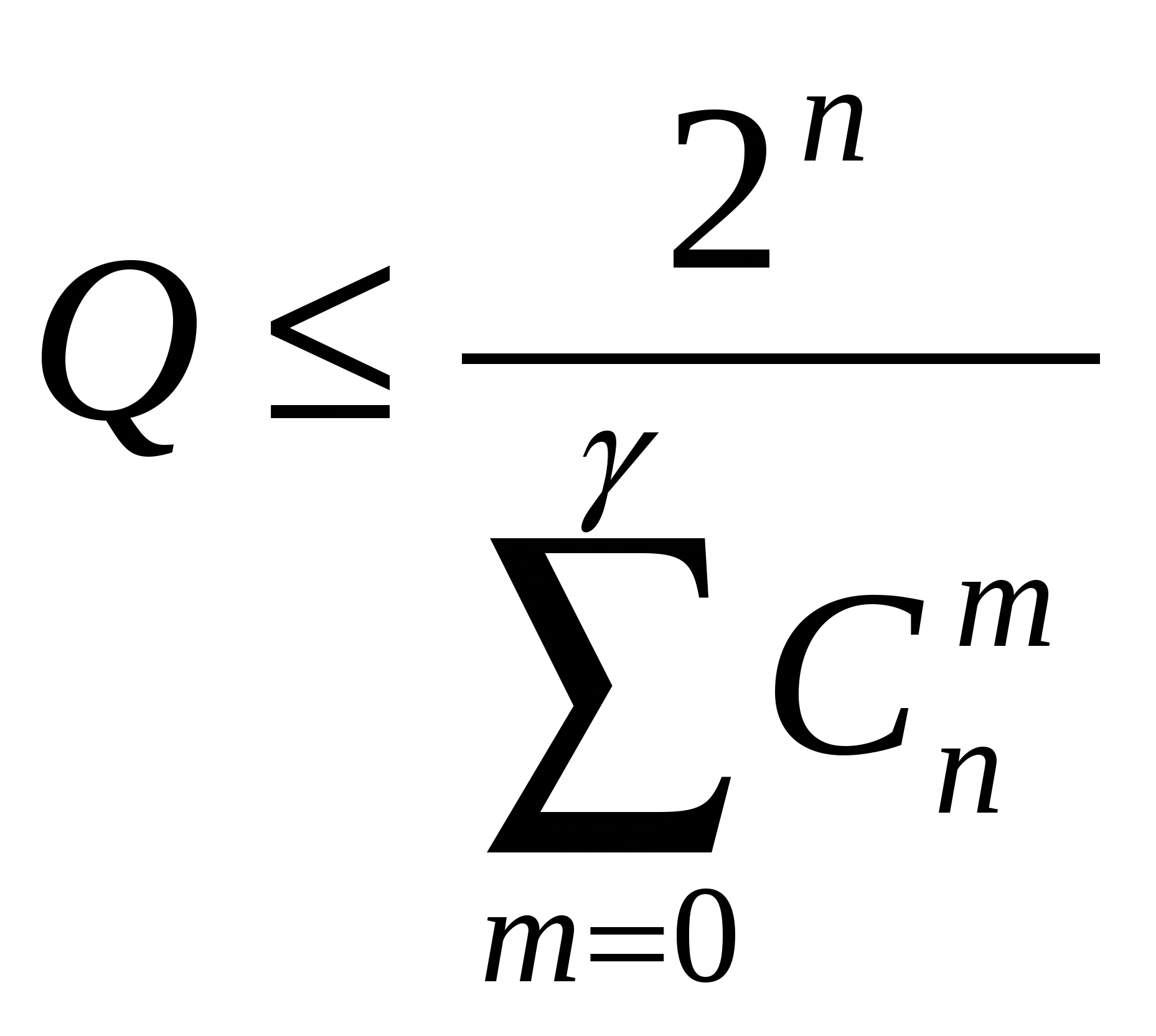. Ситуация отсутствия ошибок дает одну (исходную комбинацию). Все однократные ошибки, искажающие 1 из n разрядов, очевидно, порождают nкомбинаций. Все двукратные ошибки, искажающие 2 из nразрядов, очевидно, порождают комбинаций, где - число сочетаний из n по m. Аналогичным образом все m-кратные ошибки, искажающие m из n разрядов, порождают комбинаций. Учитывая, что формально , получаем следующую формулу для числа кодовых комбинаций, приходящихся на каждое разрешенное кодовое слово:

.Общее число кодовых комбинаций n-разрядного кода составляет , следовательно, чтобы комбинации, порождаемые из одного разрешенного кодового слова, не переходили в комбинации, порождаемые из другого, и могли быть исправлены, необходимо, чтобы число разрешенных кодовых слов Q удовлетворяло условию .

Это есть так называемая граница Хэмминга для числа разрешенных кодовых слов.

Граница Хэмминга позволяет определить минимальное число контрольных разрядов, необходимых для исправления ошибок с заданной максимальной кратностью. Пусть в n-разрядном коде k информационных разрядов, тогда число разрешенных кодовых слов составляет 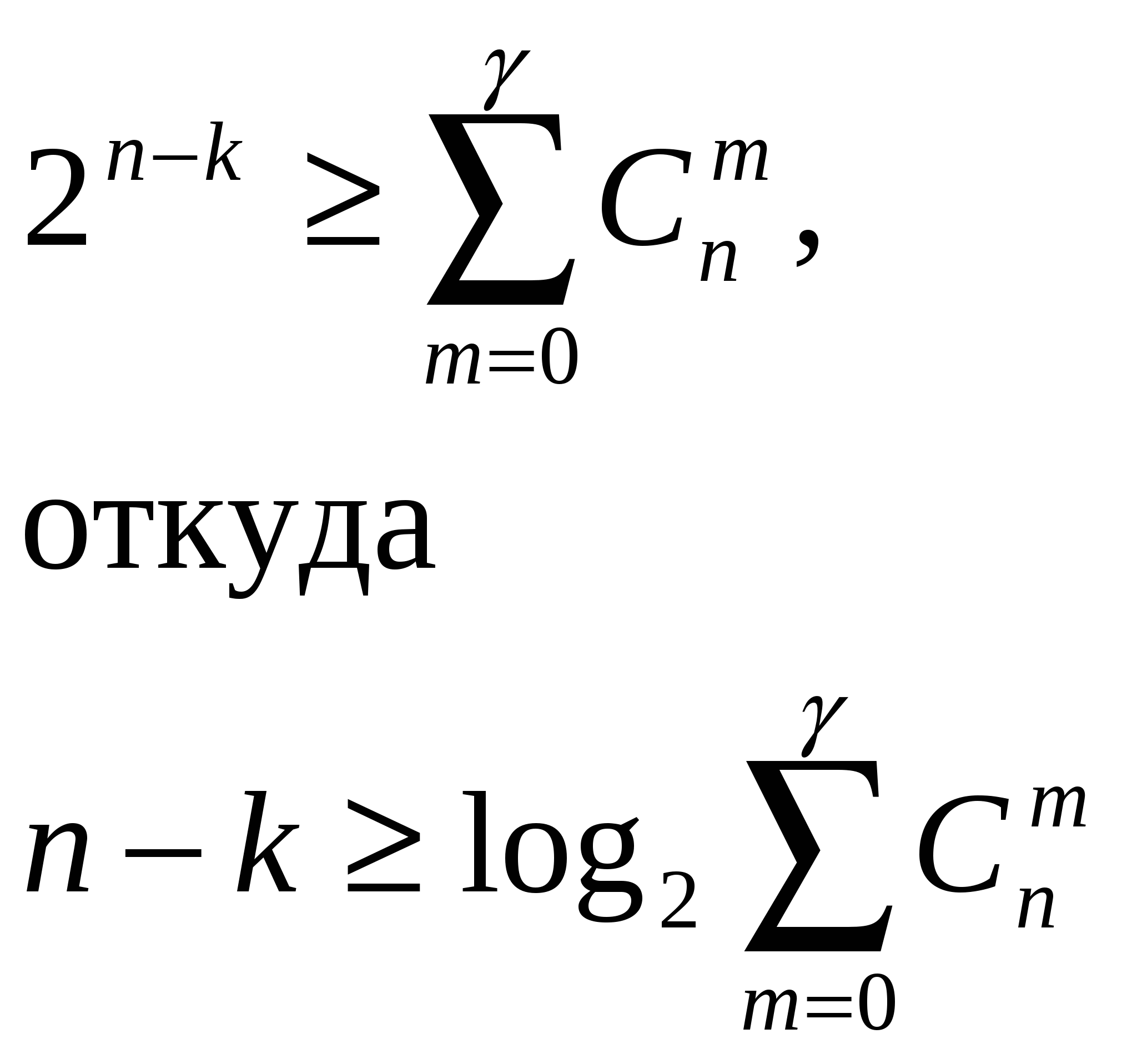. Подставляя это значение в формулу для границы Хэмминга, получаем



Величина n-k, как раз и есть минимальное число контрольных разрядов.

Коды, у которых число контрольных разрядов в точности совпадает с границей Хэмминга, называются совершенными. Совершенные коды обладают минимальной избыточностью при заданном уровне способности исправлять ошибки. В построенном выше примере 7-разрядного кода, исправляющего все однократные ошибки, использовалось 3 контрольных разряда. Подставляя параметры кода в полученную формулу, убеждаемся, что 3 – это минимальное количество контрольных разрядов, необходимое для решения задач, следовательно, код совершенный. Для более сложных случаев (большей кратности ошибок) не всегда удается построить совершенный код.

Классификация корректирующих кодов.

Математическая теория корректирующих кодов бурно развилась в 50-60-х годах XX века в обширную и практически важную самостоятельную науку, базирующуюся на казавшихся самыми абстрактными и далекими от практики разделах современной математики.

У большинства известных в настоящее время корректирующих кодов помехоустойчивость обеспечивается за счет их алгебраических свойств, в связи с чем их называют алгебраическими кодами.

Алгебраические коды подразделяются на два больших класса: блоковые и непрерывные (реккурентные).

В случае блоковых кодов кодирование заключается в сопоставлении каждому символу сообщения блока из n символов. Различают разделимые и неразделимые блоковые коды. В разделимых кодах четко разграничены информационные и контрольные (проверочные) символы. В неразделимых кодах все символы выполняют функции как информационных, так и контрольных.

Непрерывными (рекуррентными ) называются такие коды, в которых введение избыточных символов в кодируемую последовательность осуществляется без разделения её на блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Большой класс разделимых кодов составляют систематические коды, у которых значения проверочных символов определяются в результате линейных операций над определенными информационным символами. Для случая двоичных кодов каждый проверочный символ выбирается таким, чтобы его сумма по модулю 2 с определенными информационными символами стала равной нулю, т.е. обеспечивалась четность некоторой контрольной суммы. Проверочные символы могут располагаться на любом месте кодовой комбинации. Их число и соответствующие проверочные равенства (контрольные суммы) определяются тем, какие и сколько ошибок должен обнаруживать или исправлять код.

18. Помехоустойчивое кодирование. Методы помехоустойчивого кодирования.

Методы помехоустойчивого кодирования.

Рассмотрим простые практические способы построения кодов, способных обнаруживать и исправлять ошибки. Ограничимся рассмотрением двоичных каналов и равномерных кодов.

Метод контроля четности. Это простой способ обнаружения некоторых из возможных ошибок. Будем использовать в качестве разрешенных половину возможных кодовых комбинаций, а именно те из них, которые имеют четное число единиц (или нулей). Однократная ошибка при передаче через канал неизбежно приведет к нарушению четности, что и будет обнаружено на выходе канала. Очевидно, что трехкратные, пятикратные и вообще ошибки нечетной кратности ведут к нарушению четности и обнаруживаются этим методом, в то время как двукратные, четырехкратные и вообще ошибки четной кратности – нет.

Практическая техника кодирования методом контроля четности следующая. Из последовательности символов, подлежащих передаче через канал, выбирается очередной блок из k-1символов, называемых информационными, и к нему добавляется k-й символ, называемый контрольным. Значение контрольного символа выбирается так, чтобы обеспечить четность получаемого кодового слова, т.е. чтобы сделать его разрешенным.

Метод контроля четности представляет значительную ценность и широко применяется в тех случаях, в которых вероятность появления более одной ошибки пренебрежимо мала (во многих случаях, если наверняка знать, что кодовое слово принято с ошибкой, имеется возможность запросить повторную передачу). В то же время избыточность кода увеличивается минимально и незначительно при больших k(в k/( k-1)раз).

Метод контрольных сумм. Рассмотренный выше метод контроля четности может быть применен многократно для различных комбинаций разрядов передаваемых кодовых слов – и это позволит не только обнаруживать, но и исправлять определенные ошибки.

Пример:

Будем из входной последовательности символов брать по четыре информационных символа а₁а₂а₃а₄, дополнять их тремя контрольными символами а₅а₆а₇и получившееся семисимвольное слово посылать в канал. Контрольные символы будем подбирать так, чтобы были четными следующие суммы:

s₁= а₁ +а₂ +а₃ +a₅,

s₂= а₁ +а₂ +а₄ +a₆,

s₃= а₁ +а₃ +а₄ +a₇.

В каждую сумму входит по оному контрольному символу, поэтому данное требование всегда выполнимо.

Благодаря «маленьким хитростям», предусмотренным при формировании контрольных сумм, проверка их четности на выходе канала позволяет однозначно установить, была ли допущена при передаче однократная ошибка и какой из разрядов был при этом искажен (ошибками большей кратности пренебрегаем). Действительно, если один из семи символов был искажен, то, по крайней мере, одна из сумм обязательно окажется нечетной, т.е. четность всех контрольных сумм s₁, s₂, s₃ свидетельствует об отсутствии однократных ошибок. Далее, лишь одна сумма будет нечетной в том, (и только в том) случае, если искажен входящий в эту сумму один из трех контрольных символов (a₅,a₆ или a₇). Нечетность двух или трех сумм означает, что искажен тот из информационных символов а₂, а₃ или а₄, который входи в обе эти суммы. Наконец, нечетность всех трех сумм означает, что неверно принят входящий во все суммы символ а₁.

Итак, в данном примере метод контрольных сумм, увеличивая длину кода в 7/4=1,75 раза за счет введения избыточности, позволяет исправить любую однократную ошибку (но не ошибку большей кратности). Основываясь на этой идее, в принципе, можно построить коды, исправляющие все ошибки большей (но всегда ограниченной) кратности.