ВОПРОСЫ по физике. Вопросы по физике

• Название: Вопросы по физике
• Дата: 12.01.2019
• Размер: 211.51 Kb.
• Имя файла: ВОПРОСЫ по физике.docx
• Тип: Документы; #63390
• страница: 2 из 3

Если наш шарик весит 1 кг, то для удержания его на окружности понадобится центробежная сила: 

F_ц = 1·6,28²/1 = 39,4 Н2. Центробежное ускорение
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.

Во время равномерного вращательного движения меняется только направление вектора скорости, но не величина! Поэтому линейное ускорение = 0. Изменение линейной скорости поддерживается центробежным ускорением, которое направлено к центру окружности вращения перпендикулярно вектору скорости - a_ц.

Центробежное ускорение можно вычислить по формуле: a_ц = V²/R

Чем больше линейная скорость тела и меньше радиус вращения, тем центробежное ускорение больше.

17) Плоским (плоскопараллельным) движением твердого тела называется такое движение тела, при котором все его точки движутся в плоскостях параллельных некоторой неподвижной плоскости.

Плоское движение твердого тела можно разложить на поступательное движение тела вместе с некоторой точкой тела (полюсом) и вращение вокруг оси, проходящей через полюс перпендикулярно плоскости движения.

Число степеней свободы при плоском движении равно трем. Выберем точку А тела – полюс. Две координаты зададут перемещение полюса, а третья – угол поворота – вращение вокруг полюса:

,,

18) Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела (или его продолжения) остаются неподвижными в течение всего времени движения (рис.23).

Прямая, соединяющая эти точки, называетсяосью вращения. Положение тела относительно выбранной системы отсчета полностью и однозначно определяется в любой момент времени, если задано уравнение , то есть у тела одна степень свободы.

Угловая скорость, 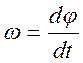 Угловое ускорение

19) В приведенных примерах оси проходят через центр инерции тела. Момент инерции относительно других осей вращения определяется при помощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а - расстояние от центра инерции тела до выбранной оси вращения,т.е.

, где m - масса тела, а - расстояние от центра инерции тела до выбранной оси вращения.Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу ,но взятому в других пределах.

20) пределим кинетическую энергию твёрдого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной скоростью υ_i=ωr_i, тогда кинетическая энергия точки

или 

Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:

(3.22)

(J - момент инерции тела относительно оси вращения)

Если траектории всех точек лежат в параллельных плоскостях (как у цилиндра, скатывающегося с наклонной плоскости, каждая точка перемещается в своей плоскости рис ), это плоское движение. В соответствии с принципом Эйлера плоское движение всегда можно бесчисленным количеством способов разложить на поступательное и вращательное движение. Если шарик падает или скользит вдоль наклонной плоскости, он двигается только поступательно; когда же шарик катится – он ещё и вращается.

Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна

(3.23)

Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.

21) Продифференцировав момент импульса по времени, получим основное уравнение динамики вращательного движения, известное как второй закон Ньютона для вращательного движения, формулируемый следующим образом: скорость изменения момента импульса L тела, вращающегося вокруг неподвижной точки, равна результирующему моменту всех внешних сил M, приложенных к телу, относительно этой точки:

dL/dt = M (14)

Так как момент импульса вращающегося тела прямо пропорционален угловой скорости  вращения, а производная d/dt есть угловое ускорение , то это уравнение может быть представлено в виде

J = M (15)

где J – момент инерции тела.
22)-

23) Гироскоп - это массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии. Земля вращается вокруг оси с запада на восток, т. е. против часовой стрелки, если смотреть на Землю с Полярной звезды (с Северного полюса). При этом угловая скорость вращения, т. е. угол, на который поворачивается любая точка на поверхности Земли, одинаков и составляет 15° за час. Линейная скорость зависит от широты: на экваторе она наибольшая – 464 м/с, а географические полюса неподвижны.

Главным физическим доказательством вращения Земли вокруг оси служит опыт с качающимся маятником Фуко. После того как французский физик Ж. Фуко в 1851 г. в парижском Пантеоне осуществил свой знаменитый опыт, вращение Земли вокруг оси стало непреложной истиной.\

24) Законы Ньютона справедливы лишь в инерциальных системах отсчета. При этом ускорение тела во всех инерциальных системах отсчета одинаково. Если некоторая система отсчета движется относительно инерциальной системы с ускорением  то такая система является неинерциальной. В этом случае ускорение телав неинерциальной системе отсчета будет отличаться от ускоренияв инерциальной системе. Ускорение в инерциальной системев этом случае равно векторной сумме ускоренийтела в неинерциальной системе иускорения самой неинерциальной системы отсчета:

Тогда сила, действующая на тело, равна . При  тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением –, т.е. так, как если бы на него действовала сила. Эту силу назовем силой инерции. Тогда по второму закону Ньютона получаем:

25) центробежная сила Земли. Эта сила всюду на поверхности Земли действует в направлении, перпендикулярном к земной оси и в сторону от нее. Центробежная сила невелика по сравнению с силой притяжения. На экваторе она достигает наибольшей величины. Но и здесь, согласно вычислениям Ньютона, центробежная сила составляет только 1/289 долю силы притяжения. Чем дальше к северу от экватора, тем меньше центробежная сила. На самом полюсе она равна нулю. На некоторой высоте центробежная сила возрастет настолько, что она будет равна силе притяжения, и сила тяжести сделается сначала равной нулю, а затем, с увеличением расстояния от Земли, примет отрицательное значение и будет непрерывно возрастать, будучи направлена в противоположную сторону по отношению к Земле.

26) Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчета из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения

27) Идеа́льная жи́дкость — в гидродинамике — воображаемая жидкость (сжимаемая или несжимаемая), в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости^[1].

35) турбуле́нтное тече́ние — явление, заключающееся в том, что, обычно, при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно, и их амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально турбулентность можно наблюдать на конце струи пара из электрочайника. Количественные условия перехода к турбулентности были экспериментально открыты английским физиком и инженером О. Рейнольдсом в 1883 году при изучении течения воды в трубах. Число́ Ре́йнольдса (. ), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса. Число Рейнольдса также является критерием подобия течения вязкой жидкости.

36) Принцип относительности Галилея гласит: Механические явления протекают одинаково во всех инерциальных системах отсчета, т. е. описывающие их законы динамики одинаковы

1. 
   37) Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.
   
2. 
   Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.
   

38) Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид: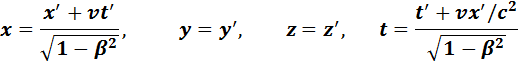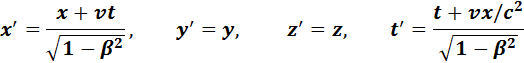





 





39) 1. Самый известный – парадокс близнецов обычно формулируется так. Пусть брат-близнец А отправляется в космический полет на звезду Х, находящуюся от нас на расстоянии, скажем, 20 световых лет. Скорость звездолета близка к скорости света: v = 0,9с. Долетев до звезды примерно за 22,3 года (по своим часам), корабль разворачивается и летит обратно. Таким образом, по часам брата А, совершившего этот полет, прошло примерно T = 44,6 года. Второй брат-близнец Б дожидался возвращения брата А на Земле. У трапа звездолета брата А встретил дряхлый старец, которому пришлось ждать встречи более 100 лет.

Собственно, здесь еще нет парадокса. Действительно, при движении со скоростью v = 0,9c лоренц-фактор равен g » 2,3 и вследствие эффекта замедления времени по часам земного наблюдателя прошло время, равное gT » 103 года.
Пусть есть две инерциальные системы отсчета – S' и S. В системе S' жесткий стержень длиной Dx' покоится вдоль оси x и нужно определить его длину в системе S, относительно которой стержень движется со скоростью v. Чтобы измерить длину стержня в любой инерциальной системе, относительно которой стержень движется вдоль продольной оси, нужно одновременно наблюдать его концы. Это – ключевое положение, непонимание которого и приводит иногда к парадоксам.

41) Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом (скаляром) в специальной и общей теории относительности.

Это свойство интервала делает его фундаментальным понятием, на основе которого может, в соответствии с принципом относительности, быть осуществлена ковариантная формулировка физических законов. В частности, преобразования Лоренца(преобразования координат, включая время, оставляющие неизменной запись всех фундаментальных уравнений физики при замене системы отсчёта) могут быть формально найдены как группа преобразований, сохраняющих интервал инвариантным

42) Релятивистское выражение для энергии

       По определению,  – импульс релятивистской частицы, а скорость изменения импульса равна силе, действующей на частицу .