Вопросы по курсу Дискретная математика

• Название: Вопросы по курсу Дискретная математика
• Дата: 18.03.2022
• Размер: 486 Kb.
• Имя файла: ex_discret.doc
• Тип: Документы; #403710
• страница: 4 из 4

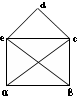Ребра: (a,b),(b,c),(c,d),(d,e),(a,e),(a,c),(a,d),(b,c),(b,d),(c,e).
В 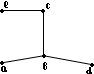управлении шоссейных дорог рассматривают проект строительства новых дорог между определенными городами. Построим граф вершины которого соответствуют городам, а ребра – дорогам. Припишем каждому между ребру вес, который равен стоимости строительства соответствующего участка дороги. Составление проекта строительства теперь можно свести к задаче построения покрывающего дерева min стоимость. Найдем его. ачинаем с самого наименьшего (a,b),(c,d),(d,e),(c,e),(a,c),(b,e),(b,d),(b,c),(a,d),(a,e).

Шаг	Ребро	Цвет	Букет1	Букет2	Вес
1	(a,b)	зеленый	a,b		5
2	(c,d)	зеленый		с,d	8
3	(d,e)	зеленый		с,a,e	10
4	(c,e)	оранжевый
5	(a,c)	зеленый	a,b,c,d,e	-	50

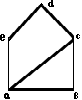
Алгоритм:

1. Выбираем вершину х_о, окрашиваем, приписываем ей значение α(х_о)=0, считаем, что у=х_о

2. Для всех вершин графа G пересчитываем все величины d(x) по следущему правилу: d(x)=min{d(x); d(y)+f(x,y)}. Для всех полученных значений d(x_i), где x_i – неокрашенные, выбираем наименьшее, значит соответствующую вершину окрашиваем, присваиваем эту вершину переменной у. Окрашиваем ребро, входящее в эту вершину и составляющую min среди всех неокрашенных вершин.

3. Если у≠x_к(у нее совпадает с конечной), то переходим к пункту 2.

Если для всех неокрашенных вершин d(x_i)=∞, то делаем вывод, что в исходном графе отсутствует кратчайший путь от вершин x₀ в x_к. Этот алгоритм позволяет находить кратчайший путь из одной вершины в другую(если он существует). При этом весовая функция, определенная на множестве ребер должна быть положительна. Ребрам могут присваиваться только положительные числа.

Свойства алгоритма.

1. Если получился кратчайший путь из вершины x₀ в неокрашенной вершине х, проходящей через вершину у, то кратчайший путь из у в х тоже будет кратчайшим.

2. Алгоритм представляет собой процедуру наращивания покрывающего дереву кратчайщих путей с корнем в вершине x₀.

13. 
    3. Получив кратчайший путь из x₀ в x_к, но остались неокрашенные вершины, то продолжая выполнять алгоритм, получим кратчайшие пути до всех неокрашенных вершин, следовательно этот алгоритм позволяет получать для исходного графа G покрывающее дерево кратчайших путей с корнем в исходной точке x₀.