Свойства разности и дополнения: 
Определение
Объединением множеств А и В называется множество, обозначаемое А  В, определяемое В, определяемое 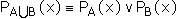
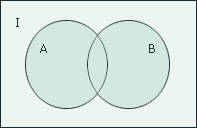
Свойства объединения множеств:
1.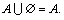
2.
3.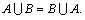
4.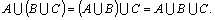
5.
6. 
Определение
Пересечением множеств А и В называется множество, обозначаемое А  В, определяемое В, определяемое 
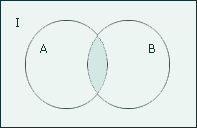
Свойства пересечения множеств:
1.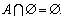
2.
3.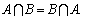
4.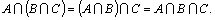
5.
6. 
Определение
Разностью множеств А и В называется множество, обозначаемое А\В, (А-В), определяемое 
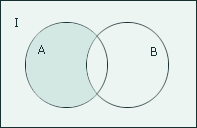
Свойства разности множеств:
1.Если тоА\В=А. тоА\В=А.
2.ЕслиАВ,тоА\В=.
3. А \ В = А \ (А В). В).
Имеют место следующие равенства:
A\Ø = A.
Ø\A = Ø.
A\I = Ø.
I\A = Ā.
A\A = Ø.
Определение
Симметрической разностью множеств А и В называют множество, обозначаемое АΔВ (А―В), определяемое AΔB ≡ (A\B)  (B\A). (B\A).

Имеет место равенство:
AΔB = (A  B)\(A B)\(A  B) B)
Имеют место следующие равенства:
АΔВ = BΔA – коммутативность.
АΔI = Ā.
АΔØ = A.
Способы задания множеств.
Способы задания множеств.
1. Перечислением своих элементов.
A={a,b,c,...}.
2. Через описание ограничительного свойства.
A={x| P(x)} - A множество таких элементов x, которые обладают свойством P(x).
В дальнейшем мы будем пользоваться общепринятыми обозначениями множеств:
N - множество натуральных чисел,
Z - множество целых чисел,
Q - множество рациональных чисел,
C - множество комплексных чисел,
R - множество действительных чисел,
 - пустое множество. - пустое множество.
Универсальное множество. (?)
Истинным, строгим или собственным подмножеством множества А называется такое его подмножество В, что В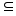 А и В А и В А. Запись В А. Запись В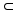 А, где А, где 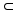 - знак строгого включения. - знак строгого включения.
По отношению к множеству А - пустое множество и само множество А называется несобственным, нестрогим или не истинным подмножествами множества А.
Таким образом, мы имеем следующие свойства множеств:
1. А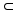 В В 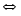 А А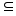 В и А В и А В. В.
2. А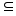 В В 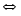 А А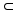 В или А=В. В или А=В.
3. А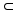 В В 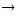 А А 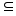 В. В.
4. А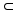 В В 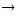 А А В. В.
5. А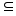 В и В В и В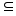 С С 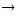 А А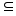 С. С.
6. А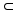 В и В В и В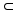 С С 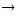 А А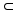 С. С.
7. А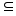 В и В В и В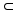 С С 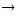 А А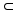 С. С.
Первые четыре свойства следуют из введенных ранее определений.
Покажем выполнение остальных свойств.
Свойство 5.
Докажем его методом от противного.
Пусть А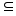 В и В В и В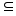 С но А С но А 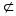 С и А С и А С. С.
Тогда существует такой элемент а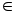 А, но а А, но а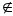 С. Тогда, т.к. В С. Тогда, т.к. В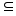 С, то а С, то а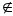 В. В.
Получили противоречие: а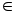 А, а А, а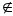 В, но А В, но А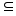 В. В.
Свойство 6.
Так как А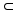 В и В В и В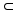 С, то по свойству 3 А С, то по свойству 3 А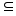 В и В В и В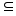 С и по свойству 5 А С и по свойству 5 А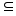 С. Осталось показать, что А С. Осталось показать, что А С. Пусть это не так и А=С . Т.е. для любого элемента а, а С. Пусть это не так и А=С . Т.е. для любого элемента а, а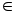 А А 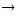 а а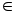 С. Так как В С. Так как В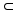 С, то В С, то В С и найдется элемент в,в С и найдется элемент в,в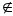 В. , но в В. , но в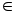 С. Так как А С. Так как А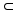 В, то в В, то в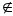 А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны. А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
Свойство 7.
Так как В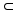 С, то по свойству 3 В С, то по свойству 3 В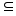 С и тогда по свойству 5 А С и тогда по свойству 5 А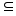 С. Осталось показать, что А С. Осталось показать, что А С. Действительно, так как В С. Действительно, так как В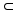 С, то найдется элемент а, а С, то найдется элемент а, а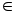 С, но а С, но а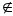 В. Так как А В. Так как А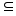 В, то а В, то а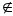 А. Отсюда а А. Отсюда а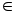 С, но а С, но а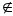 А, т.е. А А, т.е. А С. С.
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество J, то это множество называют универсальным ( для рассматриваемого набора множеств) множеством или универсом. Таким образом, универс - это такое множество, что любое рассматриваемое множество является его подмножеством.
Рассмотрим множество А={a,b,c}. Найдем все его различные подмножества. Это: пустое множество 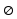 , три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или , три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или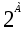 . .
Характеристическая функция множества.
Характеристической функцией ХA множества А называется одноместная функция, равная 0 на элементах множества А и 1 за пределами А. Характеристическая функция называется частичной, если она не определена за пределами А. Множество А называется примитивно рекурсивным, если его характеристическая функция примитивно рекурсивна. Множество А называется частично рекурсивным, если его характеристическая функция частично рекурсивна.
Множество А называется рекурсивно перечислимым, если существует двухместная частично рекурсивная функция ƒ(a,x) такая, что уравнение ƒ(a,x) = 0 имеет решение тогда и только тогда, когда а Î А.
Задачу кластеризации удобно формулировать использую характеристическую функцию. Характеристическая функция может принимать два значения: 0 - если элемент не принадлежит кластеру, и 1 - если элемент принадлежит кластеру. Используя характеристическую функцию, опишем кластеры следующей матрицей разбиения:
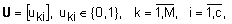 , ,
где k-ая строчка матрицы 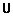 указывает на принадлежность объекта указывает на принадлежность объекта  к кластерам к кластерам 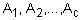 . .
Матрица 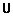 должна обладать следующими свойствами: должна обладать следующими свойствами:
 ; (12.4) ; (12.4)
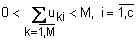 ; (12.5) ; (12.5)
Для оценки качества разбиения используется критерий разброса, показывающий сумму расстояний от объектов до центра своего кластера. Для евклидового пространства этот критерий записывается так [1]:
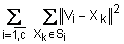 ; (12.6) ; (12.6)
где  - к-й объект кластеризации; - к-й объект кластеризации;
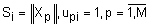 - i-й кластер; - i-й кластер;
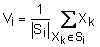 - центр i-го кластера. - центр i-го кластера.
Кластеризацию объектов 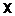 можно сформулировать как следующую задачу оптимизации: найти матрицу можно сформулировать как следующую задачу оптимизации: найти матрицу 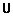 , минимизирующую значение критерия (12.6). Дискретный характер четкого разбиения приводит к трудностям нахождения оптимальной кластеризации из-за негладкости целевой функции. , минимизирующую значение критерия (12.6). Дискретный характер четкого разбиения приводит к трудностям нахождения оптимальной кластеризации из-за негладкости целевой функции.
Булеан.
Пусть А произвольное конечное n- элементное множество. Найдем мощность множества P(A), |P(А)|=   , где S={0,1,...,n}. , где S={0,1,...,n}.
Для определения величины |Р(А)| воспользуемся формулой бинома Ньютона.
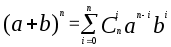 , при условиях, что a=в=1. , при условиях, что a=в=1.
Получаем,  =|P(A)|. =|P(A)|.
|
 Скачать 486 Kb.
Скачать 486 Kb.