Вопросы по курсу Дискретная математика
 Скачать 486 Kb.
|
|
Замечание. Множество  называется булеаном множества А.Декартово произведение. Кардинальными операциями называются такие операции, при применении которых в результирующем множестве появляются новые элементы. Примером кардинальных операция является прямое (декартово) произведение множеств. Прямым произведением множеств А и В называется множество А  В={(a,b)| a A, b B}, т.е. множество тех и только тех пар, первая компонента которых принадлежит множеству А, а вторая В.Через   - обозначают, соответственно, декартов квадрат и декартову n-ую степень множества А.Отношения (рефлексивности, симметричности, асимметричности, антисимметричности, транзитивности, антитранзитивности) и их свойства. Отношения эквивалентности. Функция - отображение. Отношение f на AxB называется функцией из A в B  , если  если это отображение  является функцией и выполняется условие  , то говорят, что  -если  , то функция  (f – образ множества A) - множество значенийБиекция. -отображение называется инъективным (инъекция), если из того, что  называется отображением “на”-называется сюръективным, если для любых  -отображение f называется взаимооднозначным или биекцией, если это отображение является и инъективным и сюръективным если для любого  и  :   -  если A=B, то эти отображения называются перестановкой в множестве A. Счетные множества. Счетным множеством называется всякое множество, элементам которого можно поставить во взаимно однозначное соответствие множество натуральных чисел. Отсюда, счетное множество - это бесконечное множество, элементы которого можно перенумеровать натуральными числами. Примерами счетных множеств, кроме множества натуральных чисел, являются: - множество целых чисел Z, - множество всех четных положительных (отрицательных) чисел, - множество натуральных степеней числа 2, - множество рациональных чисел Q, - множество алгебраических чисел и т.д. Покажем, например, счетность множества алгебраических чисел. Число а называется алгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами. Так как множество целых чисел счетно, то занумеруем их, например, следующим образом: если целое число n неотрицательно, то поставим ему в соответствие номер 2n+1, (1) если целое число n отрицательное, то поставим ему в соответствие номер 2|n|. Каждому уравнению вида :  (2)поставим в соответствие натуральное число:  , где 2,3,...,p - простые числа, а  - номер целого числа  (коэффициента уравнения (1)), полученного после приведенной нумерации (1).Таким образом можно перенумеровать все уравнения типа (2). Так как каждое уравнение (2) имеет не более n различных корней, то тем самым доказывается счетность множества алгебраических чисел. Свойства счетных множеств. Свойство 1. Всякое подмножество счетного множества конечно или счетно. Действительно, если А - счетное множество, то его элементы можно перенумеровать. Пусть В - подмножество множества А. Тогда, если среди элементов множества В есть элемент с наибольшим номером, то множество В является конечным, в противном случае множество В будет счетным. Свойство 2. Объединение любого конечного или счетного числа счетных множеств, есть счетное множество. Для доказательства этого свойства используется так называемая Канторовская диагональная процедура. Свойство 3. Всякое бесконечное множество содержит счетное подмножество. Действительно, если А - бесконечное множество, то в нем есть хотя бы один элемент а. Внесем его в строящееся подмножество В, присвоив этому элементу номер 1. Так как А - бесконечное множество, то в нем после удаления элемента а, останутся элементы. Возьмем любой элемент, присвоим ему номер 2, удалим его из множества А и включим его в множество В, и т.д. Построенное таким образом множество В будет счетным. Мощность множества. Несчетность множества действительных чисел. Мощность интервала (0; 1). Примеры. Элементы теории графов Понятие графа, 1.Множество точек (вершин, узлов) и множество линий (ребер, дуг), которые соединяют эти точки, называются графом. 2. Графом называется упорядоченная пара множества X (мн-во вершин) и мн-во его двухэлементных подмножеств. псевдографа, Если в графе допускаются кратные рёбра и петли, то он называется псевдографом. мультиграфа, Если в графе оказываются петли, то он называется мультиграфом. орграфа. 1. Есть мн-во точек и мн-во линий, соед эти точки, которые образуют граф, если эти линии имеют стрелки (они упорядочены), то он называется орграфом. 2. Если пары в наборе ребер упорядочены, то граф называется ориентированным. Способы задания графов. Задается множество V (вершин) и набор элементов X (рёбер), которые состоят из пар (v,w), если пара имеет вид (v,v), то это петля. Матрица смежности. Матрица инцидентности. Графы Г и Г0 можно представить в аналитической форме либо матрицей смежности А(Г), либо матрицей инцидентности В(Г). 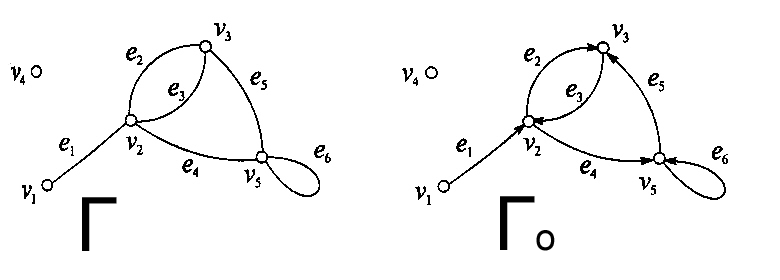 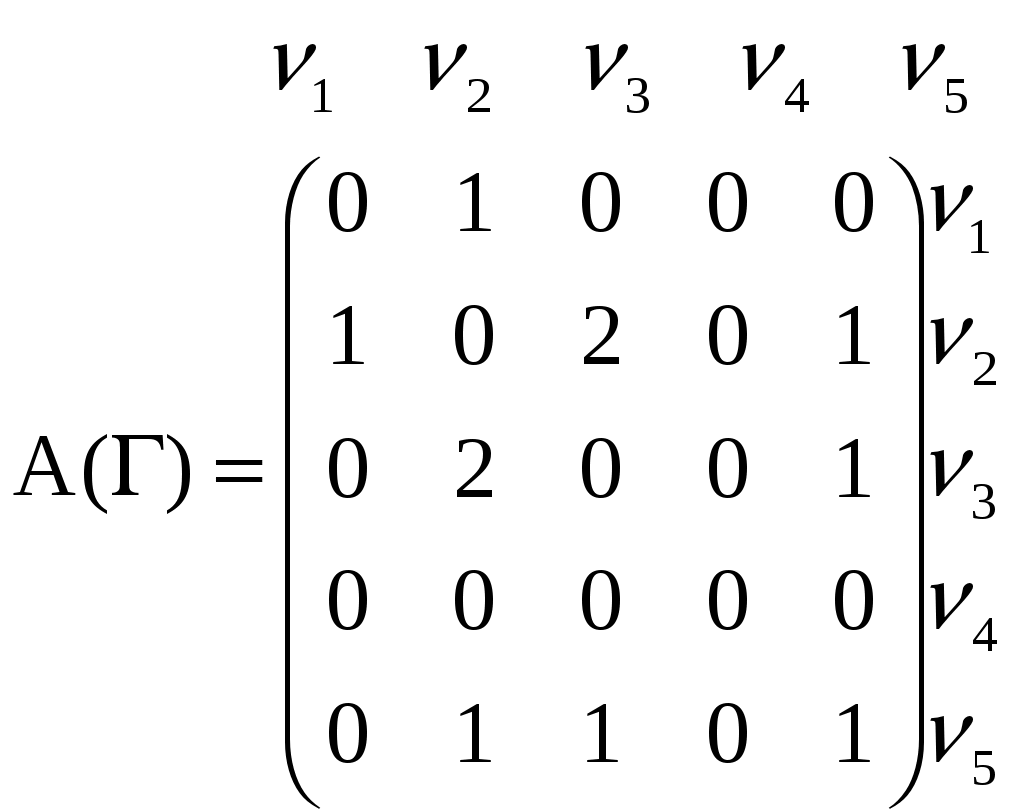 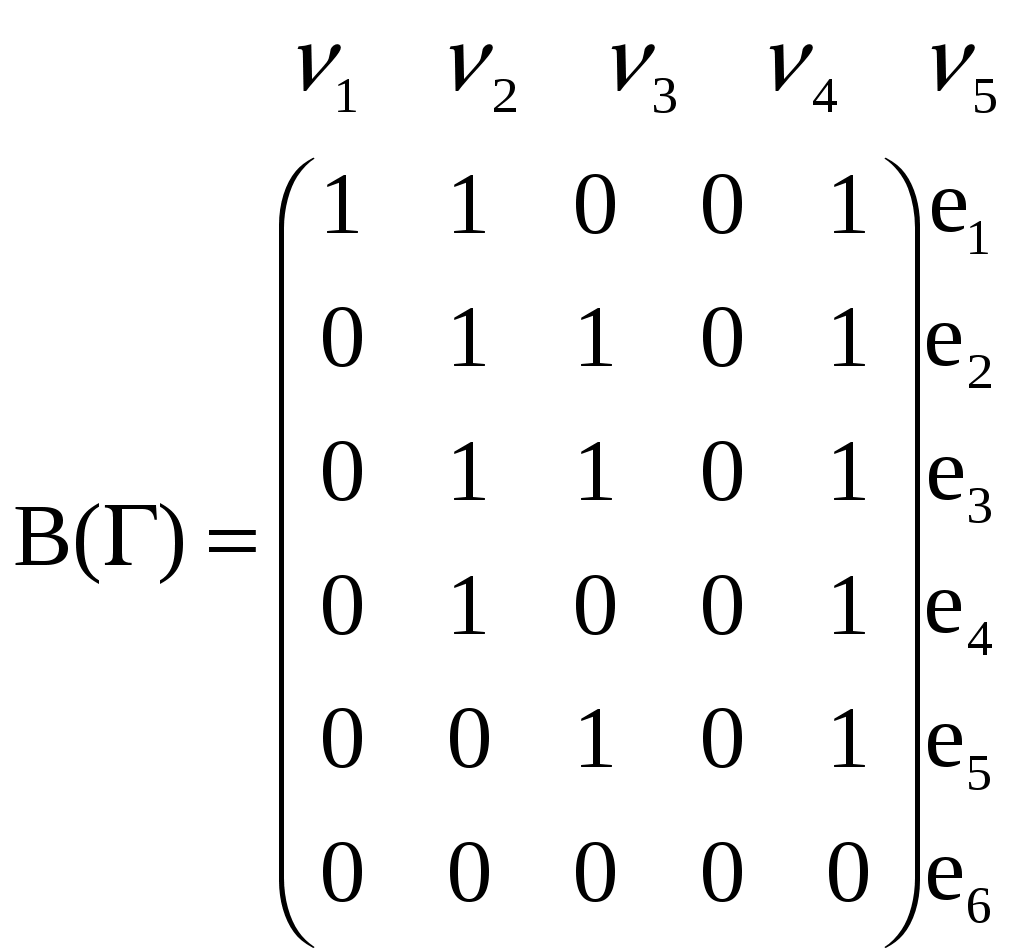 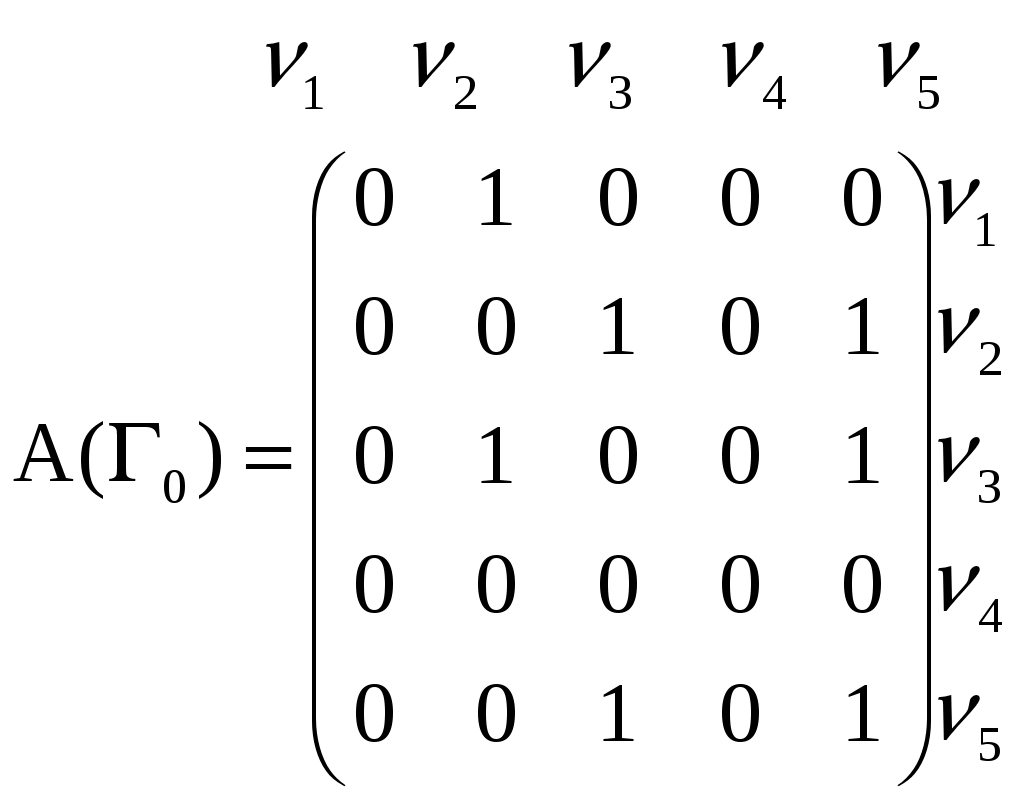 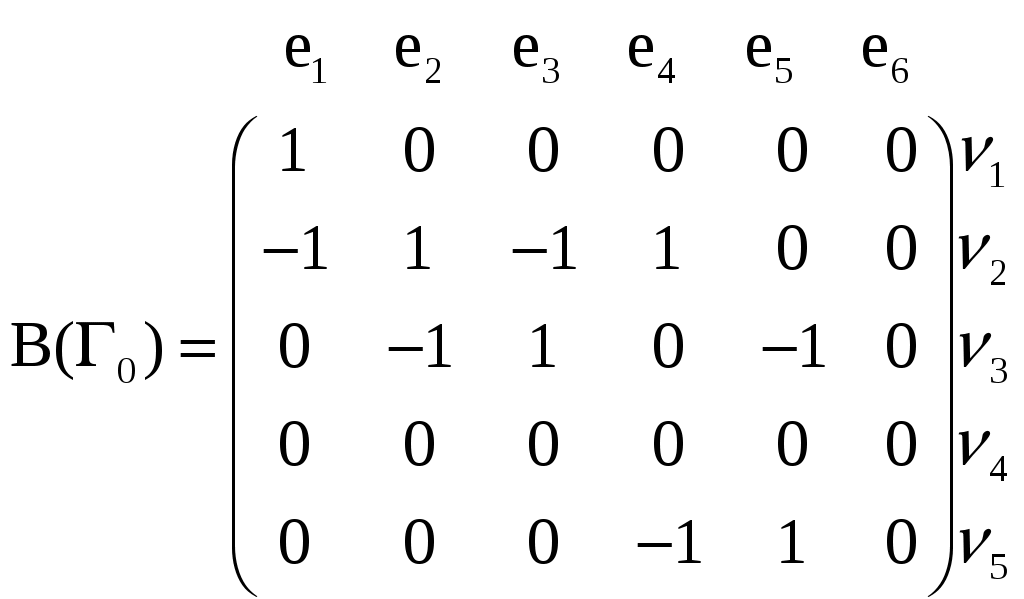 ??? возможно это то,что он задаётся отношением Геометрическое изображение графа. ???Линии (ребра графа) и точки (вершины графа). Плоский граф. Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра негде не пересекались кроме вершин.  ???в этой лекции идёт тема маршрута Полный граф. Граф называется полным, если линии такого графа образуют полную цепь (она связывает все вершины графа без образования петель и контуров) Степень вершины графа, свойства. Степенью вершины графа называется число рёбер, инцидентных данной вершине рёбер  (степень вершины a равна 2).??? Теорема о сумме степеней всех вершин графа. -в графе G порядка n сумма степеней всех его вершин есть частное число, равное  (E – число рёбер)  Теорема о числе нечетных вершин графа. Число нёчётных вершин любого графа четно. (вершина чётная, если её степень чётное число). Теорема о графе с вершинами степеней 0 и n - 1. Во всяком графе порядка n (n≥2?непонятный знак) не может быть одновременно вершин степени 0 и n-1. Маршрут, 2 определения 1-учебник, 2-тетрадь. 1.Введём понятие маршрута для графа G=(V,X) (и соответственно понятие пути для орграфа D=(V,X)). Последовательность  (где  ), в которой чередуются вершины и рёбра (дуги) и для каждого  ребро (дуга) xj имеет вид  , называется маршрутом, соединяющим вершины  (путём из  в  ), при этом называется начальной, а - конечной вершиной, а все остальные – внутренними. 2.Маршрутом, соединяющим вершины xi и xj называется такая последовательность рёбер, в которой каждые два соседних ребра инцидентны одной вершине, где начальная вершина xi и конечная xj. -Простой маршрут – когда рёбра не пересекаются. цепь, Любой минимальный путь (маршрут) является простой цепью (в ней нет повторяющихся вершин). замкнутый маршрут, Когда в маршруте есть совпадающие вершины. цикл, Если в маршруте нет совпадающих рёбер, то он называется цикл. Простой цикл – нет совпадающих вершин. их длины. ???кол-во вершин (маршрут) или кол-во рёбер (цикл). Дерево. Дерево – связанный граф, не имеющий циклов (так как любые две его вершины соединены простым путём). Корневое дерево. Иногда выделяется вершина – корень дерева. Корневое дерево - ??? Взвешенный граф. Алгоритм построения покрывающего дерева (минимального, максимального). Граф называется взвешенным, если его ребра ставятся в соответствие числа (упорядоченные наборы). Алгоритм построения покрывающего дерева. Алгоритм использует раскрашивание ребер графа в 2 цвета: ребро в зеленый, если оно включается в покрывающее дерево, иначе оно окрашивается в оранжевый. Для того чтобы ребро не окрашивалось в зеленый цвет, надо чтобы оно не образовывало цикла с ребрами, уже включенными в покрывающеее дерево. Для проверки этого из вершин ребер включенных в покрывающее дерево, образуют множество - букеты. Причем обе вершины, инцтдентные ребру, включенные в покрывающее дерево, входят в один букет, но в процессе построения покрывающего дерева может участвовать несколько букетов. Процесс построения покрывающего дерева заканчивается, когда все вершины графа включаются в один букет. Или это условие эквивалентно следущему: число окрашенных ребер должно быть на 1 меньше порядка графа. Пусть граф G не содержитпетель G=(x,e). 1. Выбираем произвольно ребро, окрашивая его в зеленый цвет. А из его кольцевых вершин образуем букет. 2. Во множестве неокрашенных ребер выбираем любое ребро и переходим к рассмотрению остальных 4 случаев: а). Но если такого ребра нет,то это значит , что граф не имеет покрывающего дерева и является не связным. Обе вершины выбранного графа принадлежат одному букету ребро, следовательно окрашиваем в оранжевый цвет и преходим на п. 2 б). Обе выбранные вершины не принадлежат ни одному букету, тогда ребро окрашиваем в зеленый цвет, а из его кольцеввых вершин образуем новый букет. в). Одна из вершин выбранного ребра принадлежит одному букету, а другая кольцевая вершина не принадлежит ни одному букету. Тогда ребро окрашиваем в зеленый цвет, а вторую кольцевую вершину включаем в тот же букет.
г). одна из вершин выбранного ребра принадлежит одному букету, а другая – другому, тогда ребро окрашивают в зеленый цвет, а букеты объединяем. 3. Если все вершины находятся в одном букете, или число окрашенных зеленым цветом ребер на 1 меньше порядка графа, то конец. Ребра зеленого цвета определяют покрывающее дерево, иначе переходим к пункту 2. Этот алгоритм обладает свойством: каждое ребро рассматривается не более одного раза, следовательно число шагов работы этого алгоритма не более числа ребер. Такие алгоритмы называют "жадными", "поедающими". Граф, имеющий покрывающее дерево - связный граф.
Пример построения покрывающего дерева: - полный граф |