Ответы на экзаменационные вопросы. Вопросы по курсу "Теплопередача"

• Название: Вопросы по курсу "Теплопередача"
• Анкор: Ответы на экзаменационные вопросы.doc
• Дата: 24.04.2017
• Размер: 329.5 Kb.
• Имя файла: Ответы на экзаменационные вопросы.doc
• Тип: Документы; #4627
• Категория: Физика
• страница: 2 из 3

6. Теплопередача через плоскую однослойную и многослойную стенку при стационарном

режиме. Средний температурный напор и методы его вычисления.
ОТВЕТ:
Стационарная теплопроводность через плоскую стенку

1).Однородная плоская стенка (Рис.9.2.).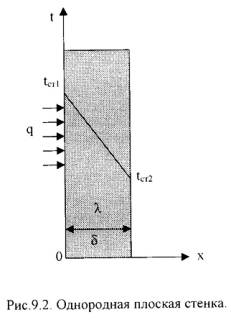


Температуры поверхностей стенки –tст1 и tст2.
Плотность теплового потока:

q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (tcт2 - tcт1)/(xcт2 - xcт1)∙
или
q = λ∙ (tcт2 - tcт1)/(xcт2 - xcт1)∙ Dt/Dx (9.13)

Тогда

q = λ/δ∙(tст1 – tст2) = λ/δ∙Δt, (9.14)

Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м2∙К)/Вт], то плотность теплового потока:

q = (tст1 – tст2)/R . (9.15)

Общее количество теплоты, которое передается через поверхность F за время τ определяется:

Q = q∙F∙τ = (tст1 – tст2)/R·F∙τ . (9.16)

Температура тела в точке с координатой х находится по формуле:

tx = tст1 – (tст1 – tст2)∙x/ δ . (9.17)

2).Многослойная плоская стенка.
Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенокtст1 и tст2, коэффициенты теплопроводности слоевλ1, λ2, λ3, толщина слоевδ1, δ2, δ3.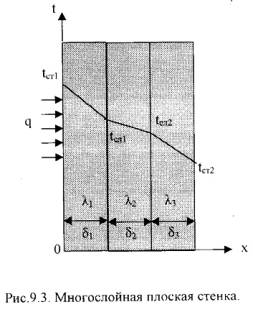


Плотности тепловых потоков через каждый слой стенки:

q = λ1/δ1∙(tст1 – tсл1) , (9.18)
q = λ2/δ2∙(tсл1 – tсл2) , (9.19)
q = λ3/δ3∙(tсл2 – tст2) , (9.20)

Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t1 – t4)/(δ1/λ1 + δ2/λ2 + δ3/λ3) = (tст1 – tст4)/Ro , (9.21)

где: Ro = (δ1/λ1 + δ2/λ2 + δ3/λ3) – общее термическое сопротивление теплопроводности многослойной стенки.
Температура слоев определяется по следующим формулам:

tсл1 = tст1 – q∙(δ1/λ1). (9.22)
tсл2 = tсл1 – q·δ2/λ2). (9.23)

Температурный напор - разность характерных температур среды и стенки (или границы раздела фаз) или двух сред, между которыми происходит теплообмен. Местный Температурный напор — разность температур среды и местной температуры стенки (границы раздела фаз) либо разность температур двух сред в данном сечении теплообменной системы. Средний Температурный напор — Температурный напор, осреднённый по поверхности теплообмена. Произведение значения Температурный напор на коэффициент теплопередачи определяет количество теплоты, передаваемое от одной среды к другой через единицу поверхности нагрева в единицу времени, то есть плотность теплового потока.

Тепловой_поток._ОТВЕТ'>7. Решение задачи определения температурного поля однослойной цилиндрической стенки при стационарном режиме в граничных условиях первого рода. Тепловой поток.
ОТВЕТ:

Тепловой поток - количество теплоты, переданное через изотермическую поверхность в единицу времени. Размерность Т. п. совпадает с размерностью мощности. Т. п. измеряется в ваттахили ккал/ч (1 вт = 0,86 ккал/ч). Т. п., отнесённый к единице изотермической поверхности, называется плотностью Т. п., удельным Т. п. или тепловой нагрузкой; обозначается обычно q, измеряется в вт/м² или ккал/(м²ч). Плотность Т. п. — вектор, любая компонента которого численно равна количеству теплоты, передаваемой в единицу времени через единицу площади, перпендикулярной к направлению взятой компоненты.

8. Теплопередача через однослойную и многослойную цилиндрическую стенку при стационарном режиме. Критический диаметр изоляции. Пути интенсификации теплопередачи.
ОТВЕТ:
Стационарная теплопроводность через цилиндрическую стенку

1). Однородная цилиндрическая стенка.
Рассмотрим однородный однослойный цилиндр длиной l, внутренним диаметром d1и внешним диаметром d2 (Рис.9.4).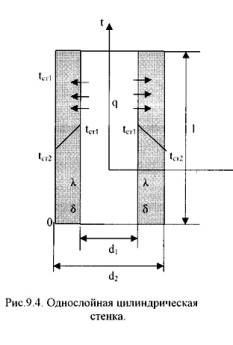


Температуры поверхностей стенки –tст1 и tст2.
Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r (9.24)илиQ = 2·π·λ·l·Δt/ln(d2/d1), (9.25)где: Δt = tст1 – tст2 – температурный напор;
λ – κоэффициент теплопроводности стенки.
Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:ql = Q/l =2·π·λ·Δt /ln(d2/d1), [Вт/м]. (9.26)Температура тела внутри стенки с координатойdх:tx = tст1 – (tст1 – tст2) ·ln(dx/d1) / ln(d2/d1). (9.27)2). Многослойная цилиндрическая стенка.
Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).

Температура внутренней поверхности стенки –tст1, температуранаружнойповерхности стенки –tст2, коэффициенты теплопроводности слоев -λ1, λ2, λ3, диаметры слоев d1, d2, d3, d4.
Тепловые потоки для слоев будут:
1-й слойQ = 2·π· λ1·l·(tст1 – tсл1)/ ln(d2/d1), (9.28)
2-й слой
Q = 2·π·λ2·l·(tсл1 – tсл2)/ ln(d3/d2), (9.29)
3-й слой
Q = 2·π·λ3·l·(tсл2 – tст2)/ ln(d4/d3), (9.30)Решая полученные уравнения, получаем для теплового потока через многослойную стенку:Q = 2·π·l·(tст1 – tст2) / [ln(d2/d1)/λ1 + ln(d3/d2)/λ2 + ln(d4/d3)/λ3]. (9.31)Для линейной плотности теплового потока имеем:ql = Q/l = 2·π· (t1 – t2) / [ln(d2/d1)/λ1 + ln(d3/d2)/λ2 + ln(d4/d3)/λ3]. (9.32)Температуру между слоями находим из следующих уравнений:

tсл1 = tст1 – ql·ln(d2/d1) / 2·π·λ1 . (9.33)
tсл2 = tсл1 – ql·ln(d3/d2) / 2·π·λ2 . (9.34)

9. Теплопроводность при нестационарном режиме неограниченной плоской стенки в граничных условиях третьего рода. Использование метода обобщенных переменных для представления результатов решения. Физический смысл чисел Фурье и Био. Влияние числа Био на температурное поле.
ОТВЕТ:
Для распространения тепла в твёрдом теле характерны П. к.: Фурье число Fo = at/l² и число Био Bi = l/. Число Bi определяет характер соответствия между температурными условиями в окружающей среде и распределением температуры в теле.

10. Метод обобщенных переменных. Обобщенные переменные и обобщенное уравнение для теплоотдачи. Физический смысл чисел Rе, Еu, Рr, Gа, Аr, Gr, Ре, Рr, Nu.
ОТВЕТ:

1.      Подобие граничных условий (подобие процессов теплопереноса на границе между стенкой и потоком жидкости) характеризуется критерием Нуссельта:



Nu является мерой соотношения толщины пограничного слоя и определяющего геометрического размера (для трубы – её диаметр d).

2. Условие подобия в ядре потока выражает критерий Фурье (равенство критериев Фурье в сходственных точках тепловых потоков - необходимое условие подобия неустановившихся процессов теплообмена):



3. Критерий Фурье является аналогом критерия гомохронности Ho при гидродинамическом подобии (учитывает неустановившийся характер движения в подобных потоках).



4. Критерий Пекле является мерой соотношения между теплом, переносимым путём конвекции и путём конвекции и путём теплопроводности при конвективном теплообмене:



5. Критерий Рейнольдса отражает влияние силы трения на движение жидкости (характеризует отношение инерционных сил к силам трения в подобных потоках):



6. Критерий Фруда отражает влияние силы тяжести, или собственного веса, на движение жидкости (является мерой отношения силы инерции к силе тяжести в подобных потоках):



Необходимыми условиями подобия процессов переноса тепла является соблюдение гидродинамического (характеризуется равенством критериев Ho, Re, Fr в сходственных точках подобных потоков)и геометрического подобия (характеризуется постоянством отношения основных геометрических размеров стенки L1, L2, …Ln к некоторому характерному размеру L0 = d – обычно диаметру трубы).

Таким образом, обобщённое (критериальное) уравнение конвективного теплообмена выражается функцией вида:



или с учётом того, что критерий Нуссельта является определяемым, так как в него входит искомая величина коэффициента теплоотдачи:



7.

где - критерий Прандтля (характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена) является мерой подобия полей температур и скоростей).

Значения критерия Прандтля для капельных жидкостей порядка 3 – 300 и значительно уменьшаются с возрастанием температуры, а для газов постоянны и зависят от атомности газа (Pr 0.7 – 1). Поэтому для жидкостей тепловой подслой тоньше гидродинамического.

С введением критерия Pr обобщённое уравнение конвективного теплообмена принимает вид



При установившемся процессе теплообмена из обобщённого уравнения исключаются критерии Fo и Ho. При вынужденном движении, когда влияние сил тяжести на гидродинамику потока, отдающего или воспринимающего тепло, пренебрежимо мало, влиянием критерия Fr на теплоотдачу можно пренебречь. Тогда:



вид этой функции определяется опытным путём, причём обычно ей придают степенную форму. Так, например, при движении потока в трубе диаметром d и длиной l может быть представлено в виде:



где С, m, n, p – величины, определяемые из опыта.

8. До сих пор обсуждались задачи с вынужденным движением жидкости. Рассмотрим, например, процесс нагревания воды в кастрюле. В этом случае нельзя исключить из уравнения критерий Фруда, т.к. сила тяжести служит причиной воздействия естественной конвекции. Однако для расчёта критерия Fr необходимо знать скорость движения конвективных токов жидкости, определить которую весьма сложно. Попробуем исключить скорость, комбинируя критерии Fr и Re:



Полученный безразмерный комплекс величин называют производным критерием Галилея:



9. Умножив критерий Ga на безразмерную разность плотностей нагретой и холодной жидкости, являющуюся причиной естественной конвекции, получим критерий Архимеда:



10. Т.к. изменение плотности при нагревании связано с коэффициентом объёмного расширения , можем заменить разность плотностей разностью температур:



подставив это выражение в критерий Архимеда, получим критерий для характеристики теплоотдачи в условиях естественной конвекции – критерий Грасгофа (мера отношения сил трения к подъёмной силе, определяемой разностью плотностей в различных точках неизотермического потока):



Следовательно, для процессов теплоотдачи при естественной конвекции, или свободном движении жидкости, обобщённое уравнение теплоотдачи имеет вид:



Для газов Pr1=const и, значит, критерий Pr можно исключить из обобщённых уравнений для определения

11. Понятие о динамическом пограничном слое. Дифференциальные уравнения динамического ламинарного пограничного слоя.
ОТВЕТ:
Динамический пограничный слой – это тонкий слой жидкости у поверхности обтекаемого тела, в котором силы инерции и силы вязкости имеют одинаковый порядок, а это значит что по толщине этого слоя наблюдается существенные перепады скорости, следовательно перепады по касательным напряжениям. Весь поток, обтекающий твердую поверхность можно разделить на 2 области:

1. область динамического пограничного слоя с существенной вязкостью.

2. внешнюю область, так называемую потенциального течения, где силами вязкости можно пренебречь.

12. Понятие о тепловом пограничном слое. Система дифференциальных уравнений ламинарного пограничного слоя.
ОТВЕТ:
Из-за разности температуры жидкости и температуры стенки помимо динамического пограничного слоя образуется тепловой пограничный слой, в котором теплопроводность соизмерима с конвективной теплоотдачей, при этом по толщине этого слоя наблюдается существенный градиент температуры.


13. Турбулентный перенос теплоты и количества движения. Представление о турбулентном течении как результате наложения пульсационного течения на среднее. Простейшая модель турбулентного потока по Прандтлю.
14. Продольное обтекания пластины. Теплоотдача при ламинарном пограничном слое Обобщенное уравнение. Зависимость теплоотдачи от изменения физических свойств жидкости.

15. Продольное обтекания пластины. Число Стантона и его физический смысл. Связь

между коэффициентом теплоотдачи и коэффициентом трения (аналогия переноса теплоты и

количества движения).

16. Продольное обтекания пластины. Теплоотдача при турбулентном пограничном слое.

Схема турбулентного пограничного слоя. Обобщенное уравнение для теплоотдачи. Изменение коэффициента теплоотдачи вдоль пластины.

17. Теплоотдача при вынужденном движении в трубах. Режимы течения. Начальный

участок гидродинамической и тепловой стабилизации. Изменение коэффициента теплоотдачи

по длине трубы.

18. Теплоотдача при ламинарном течении жидкости в трубах. Вязкостный вязкостногравитационный режимы течения. Структура обобщенных уравнений. Учет зависимости физических свойств жидкости от температуры. Учет влияния свободной конвекции.
ОТВЕТ:
Теплоотдача при ламинарном движении жидкости в трубах.

Ламинарный режим течения наблюдается при малых скоростях потока и малых диаметрах канала.

Турбулентный режим течения наблюдается при больших скоростях потока и больших диаметрах канала.

Скорость перехода потока от ламинарного режима к турбулентному называется критической и определяется соотношением скорости течения и диаметра трубы.

Для ламинарного режима характерно параболическое распределение скорости течения

Перенос тепла от одного слоя жидкости к другому по нормали к стенке в основном осуществляется теплопроводностью, в тоже время каждый слой жидкости имеет различную скорость движения вдоль оси, при этом теплота вдоль потока передается конвекцией. В следствии этого теплообмен при ламинарном режиме сильно зависит от гидродинамической картины течения.

Зададимся следующими условиями: пусть на входе в трубу температура жидкости t_f постоянна и отличается от температуры стенки t_w, по мере движения потока т-ра жидкости меняется и образуется пограничный слой. На некотором расстоянии от начала трубы тепловые пограничные слои смыкаются и в теплообмене участвует весь поток

На практике л.р.т. встречается у очень сильно вязких жидкостей (нефть, масло), в которых число Pr значительно выше 1. в этом случае длина начального участка довольно большая, и при Re 200-500 длина такого участка может достигать 5000 d трубы. При этом в пределах начального теплового участка т-рный градиент в жидкости убывает т .к. температурный напор уменьшается, но центральная часть потока в теплообмене не участвует,=> локальный коэффициент теплоотдачи по длине начального участка уменьшается до того момента как пограничные слои сольются, дальше к-т теплоотдачи принимает некоторое постоянное среднее значение.
19. Теплоотдача при турбулентном течении жидкости в трубах. Структура обобщенного уравнения. Учет зависимости физических свойств жидкости от температуры.

20. Теплоотдача при поперечном обтекании одиночного цилиндра. Явление отрыва. Локальный и средний коэффициенты теплоотдачи. Структура обобщенного уравнения.

21. Теплоотдача при поперечном обтекании пучков труб. Особенности процесса Структура обобщенного уравнения.