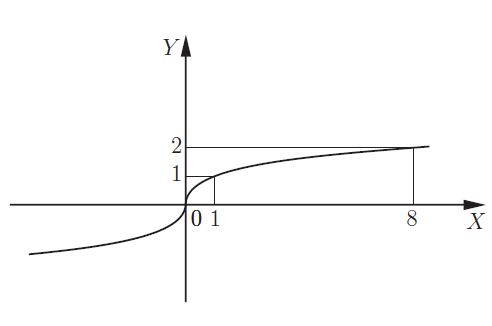функция вся теория. _Функции (вся теория). Вот необходимая теория для решения задания 10 егэ
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
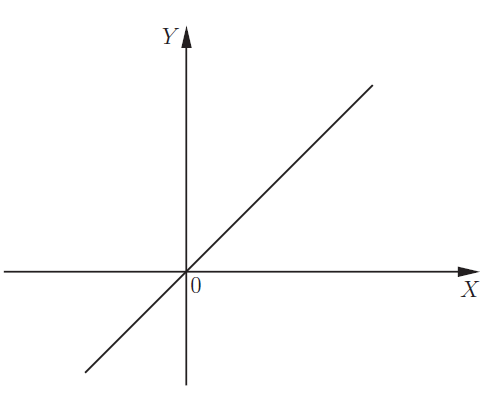
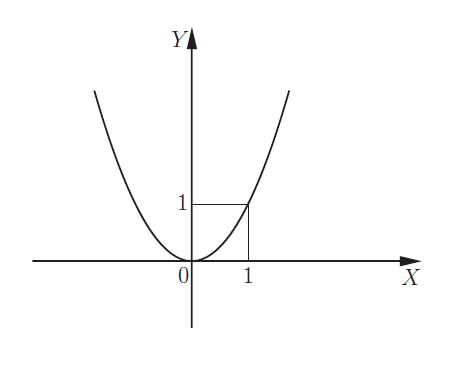
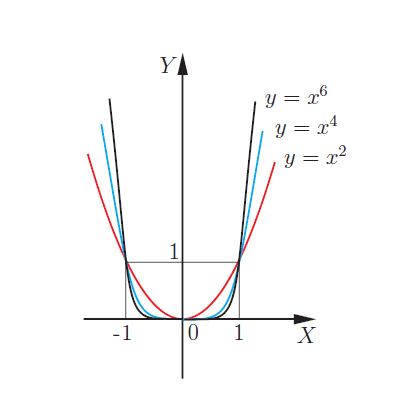
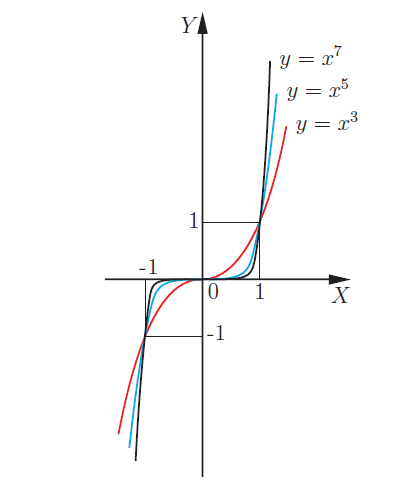
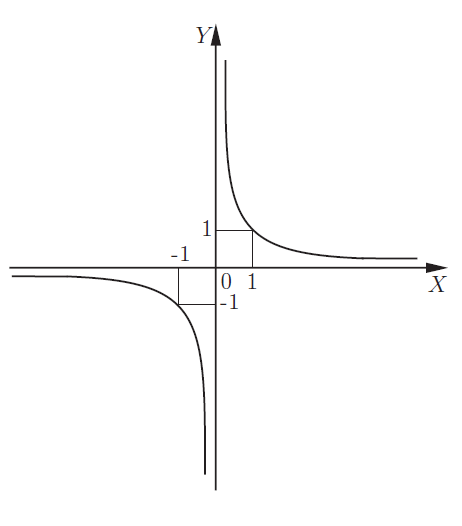
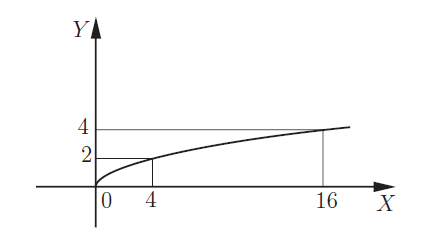
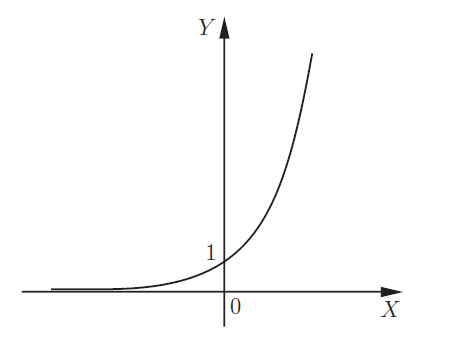
Вот необходимая теория для решения задания №10 ЕГЭ. Что такое функция Чтение графика функции Четные и нечетные функции Периодическая функция Обратная функция 5 типов элементарных функций и их графики Преобразование графиков функций 1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.. Знакомое вам обозначение Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества. Например, функция способы задания функции. А) С помощью формулы. Б) Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. С) С помощью таблицы Д) С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция 2. Чтение графика функции На рисунке изображен график функции область определения функции область значений функции нули функции промежутки возрастания и убывания точки максимума и минимума наибольшее и наименьшее значение функции на отрезке. 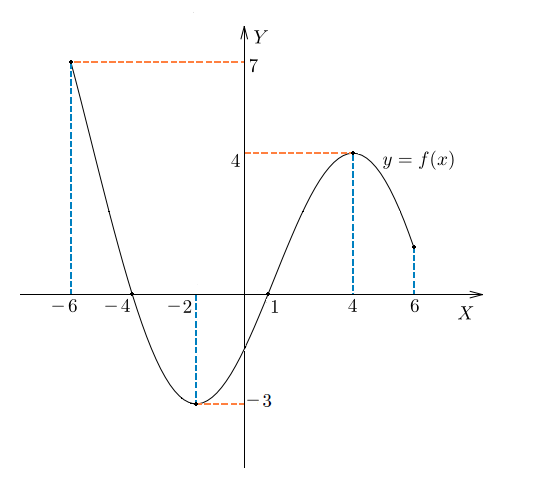 3Четные и нечетные функции Функция График четной функции симметричен относительно оси ординат. Например, 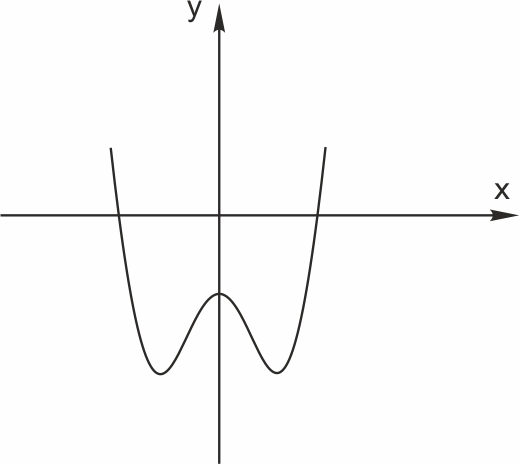 Функция График нечетной функции симметричен относительно начала координат. Например, 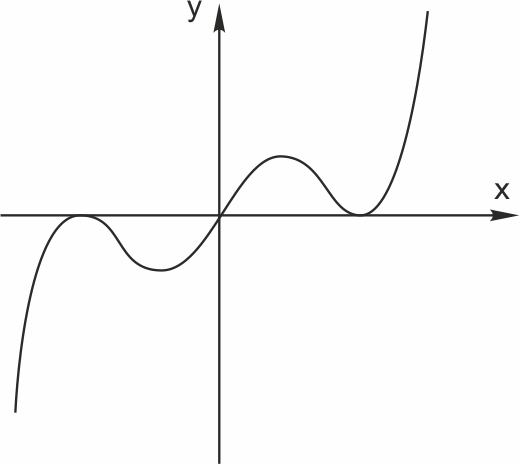 Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания: 1. Проверьте, является ли функция Область определения функции Проверим, является ли 2. Проверьте, является ли функция Область определения: все действительные числа. Её график симметричен относительно оси y. 3. Проверьте, является ли функция Область определения функции симметрична относительно нуля. — чётная, её график симметричен относительно оси y. 4.Периодическая функция Это функции, все значения которых повторяются через определенный период. Как будто мы копируем часть графика — и повторяем на всей области определения функции. Например, 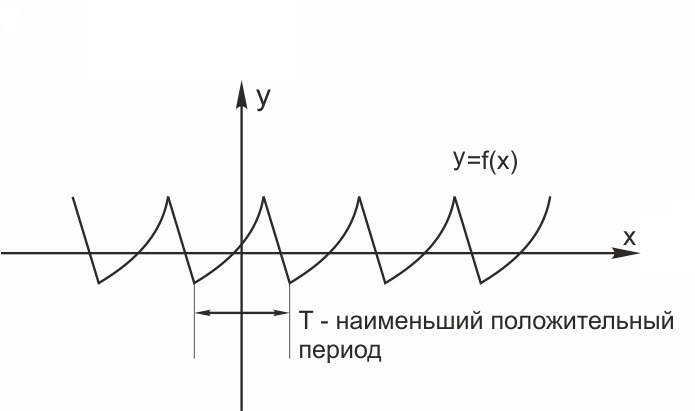 Функция Например, Для функций Для функций Наименьший положительный период суммы функций равен наименьшему общему кратному периодов слагаемых. 5.Обратная функция Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями. Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x. Например, Сделали действие (возвели Другой пример взаимно-обратных функций: показательная и логарифмическая. Помните основное логарифмическое тождество: Графики взаимно-обратных функций симметричны относительно прямой у = x. То, что для функции является областью определения, для обратной функции будет областью значений. 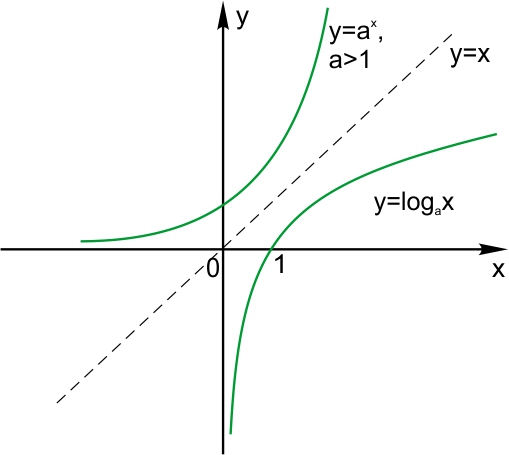 6. 5 типов элементарных функций и их графики Существует всего пять типов элементарных функций: 1).Степенные К этому типу относятся линейные, квадратичные, кубические, Все они содержат выражения вида xα. 2)Показательные Это функции вида y = ax 3)Логарифмические y = logax. 4)Тригонометрические В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы. 5)Обратные тригонометрические Содержат arcsinx, arccosx, arctgx, arcctgx. Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
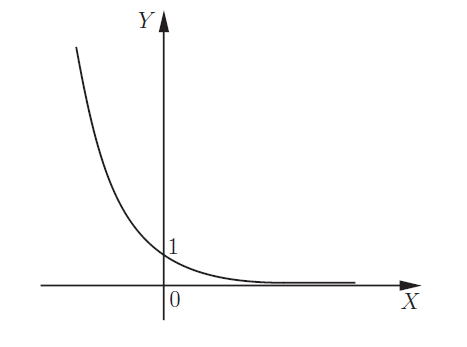
Показательная функция y = ax
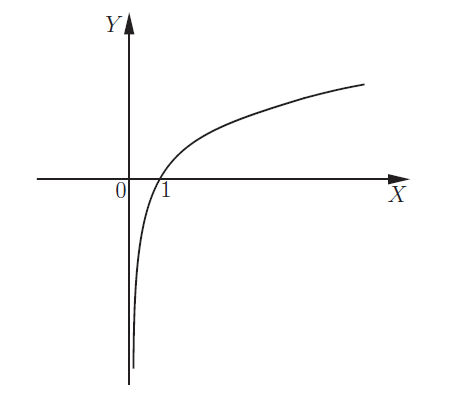
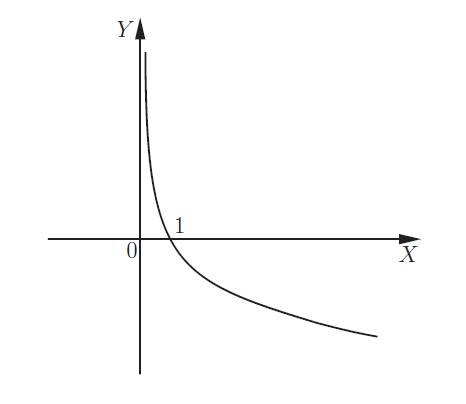
Логарифмическая функция y = logax
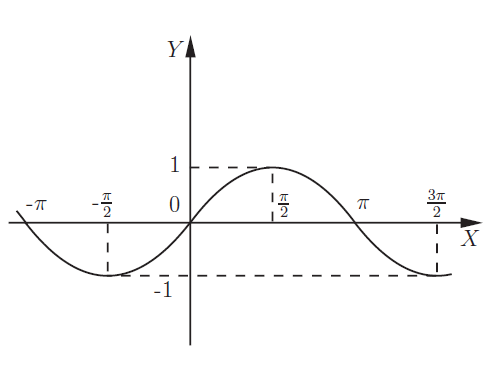
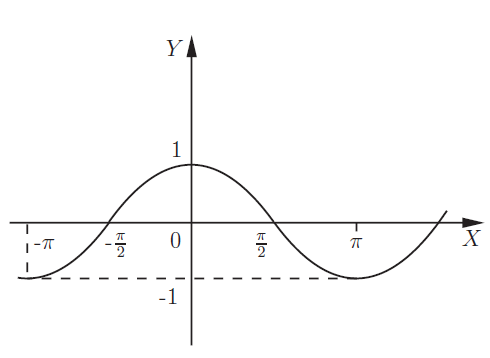
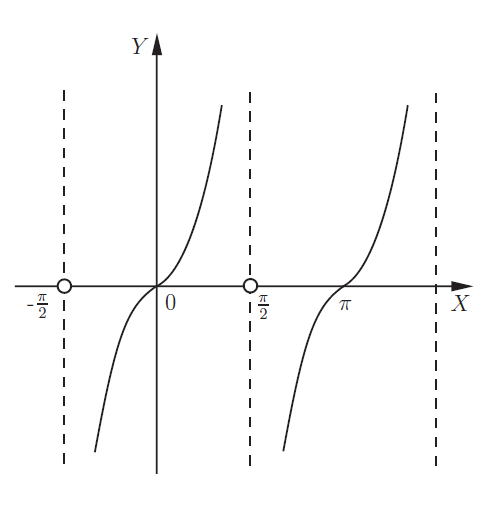
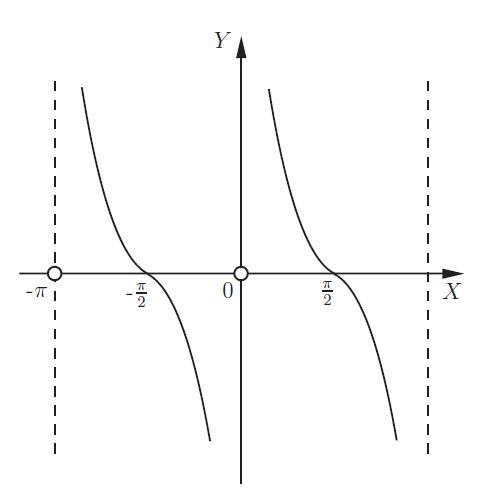
Тригонометрические функции
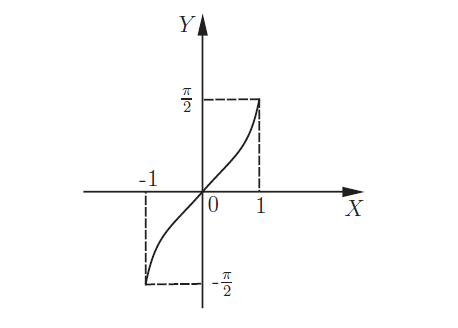
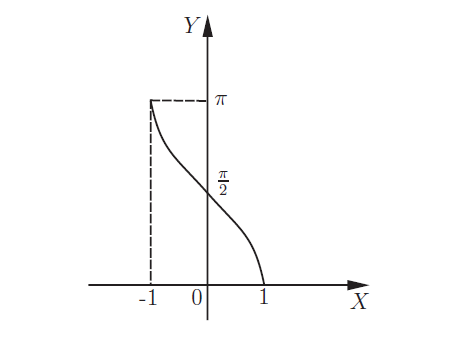
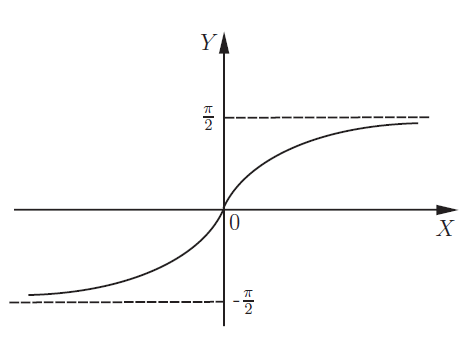
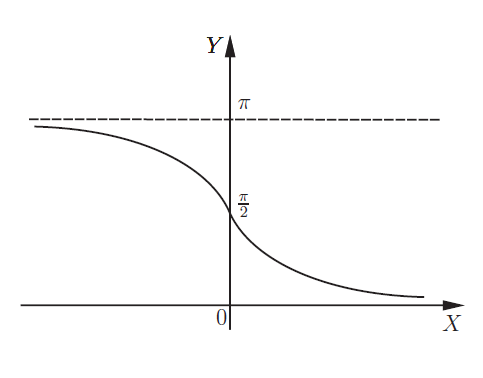
Обратные тригонометрические функции
Сдвиг по горизонтали. Пусть функция задана формулой 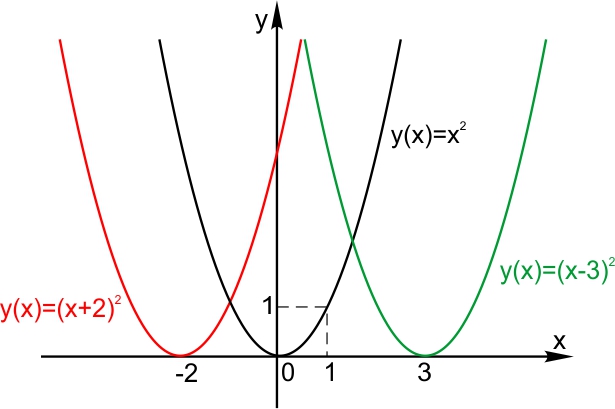 Сдвиг по вертикали. Пусть функция задана формулой 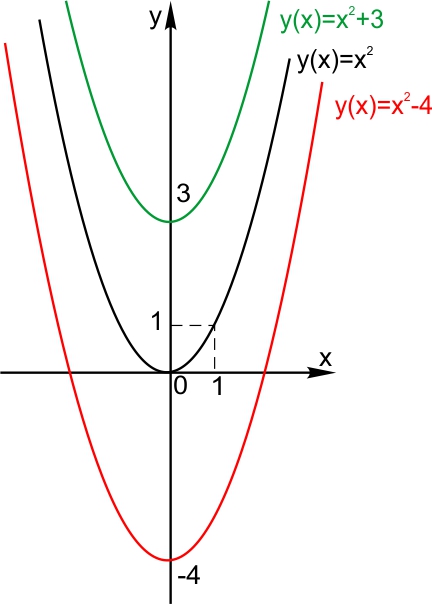 2. Растяжение (сжатие) по горизонтали. Пусть функция задана формулой 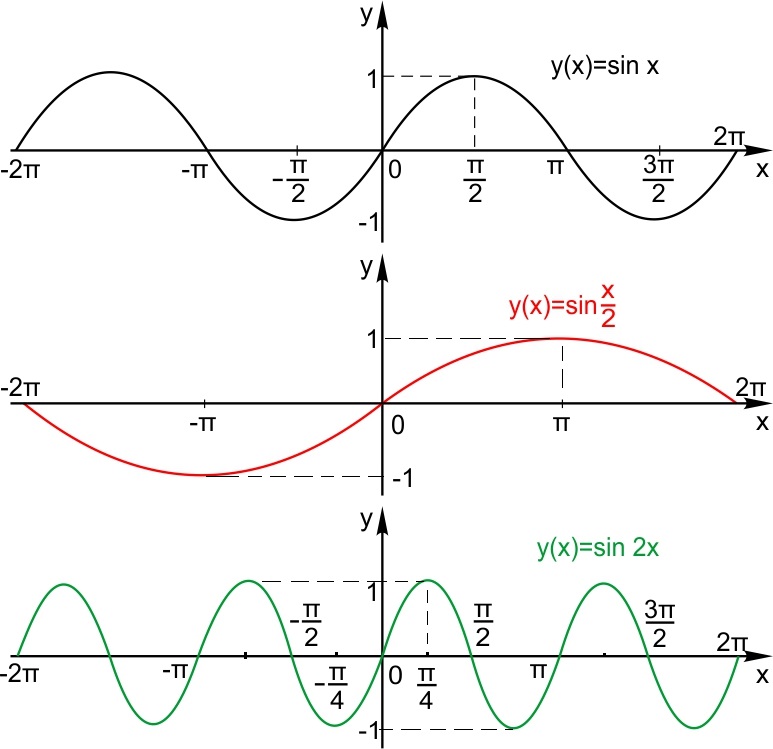 3. Растяжение (сжатие) по вертикали Пусть функция задана формулой 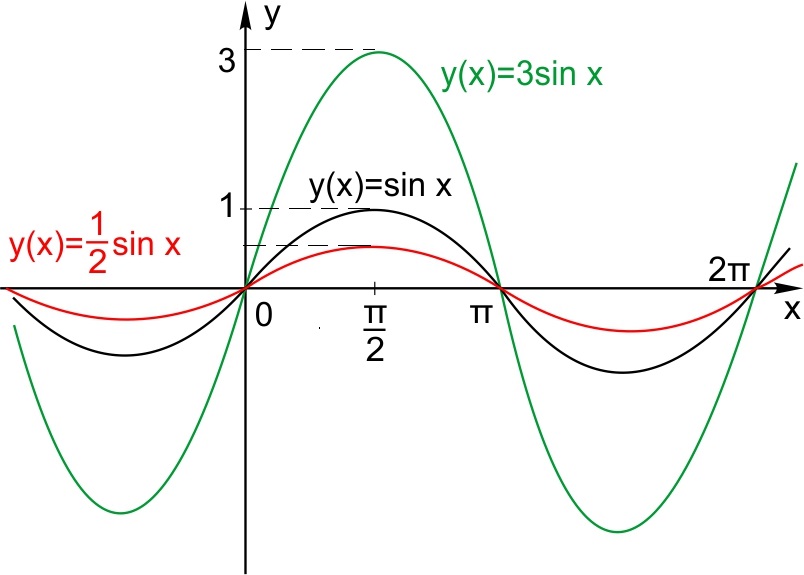 4. Отражение по горизонтали График функции 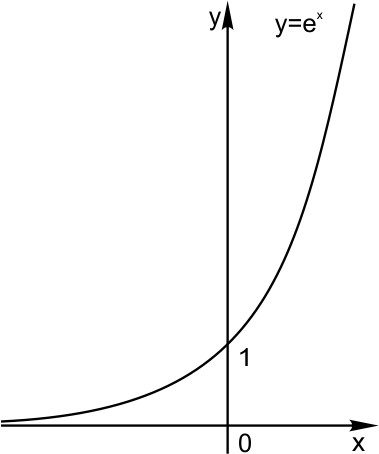 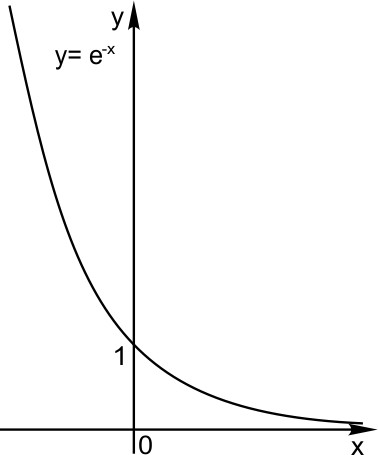 5. Отражение по вертикали. График функции 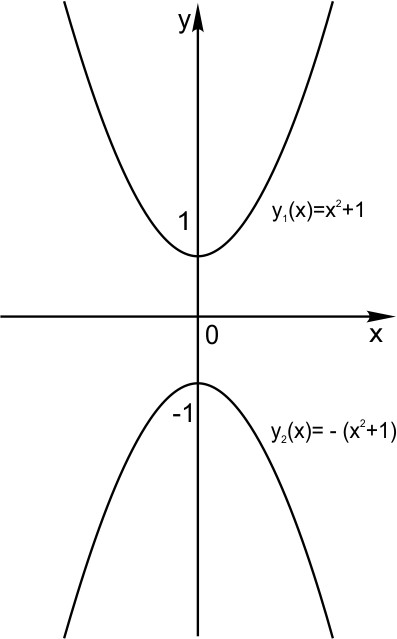 6. Графики функций |