адамар. Вот несколько примеров матриц Адамара

• Название: Вот несколько примеров матриц Адамара
• Дата: 14.12.2018
• Размер: 60.72 Kb.
• Имя файла: адамар.docx
• Тип: Документы; #60294

Жак Адамар — французский математик-универсал. Автор множества фундаментальных работ по алгебре, геометрии, функциональному анализу, дифференциальной геометрии, математической физике, топологии, теории вероятностей, механике, гидродинамике и др. Родился 8 декабря 1865 г. в Версале в еврейской семье. В детстве увлекался языками, был победителем конкурса знатоков греческого и латинского языков. Среднее образование Жак Адамар получил в лицее Людовика Великого. Некоторое время учился в Политехнической школе. В 1890 г. окончил Высшую нормальную школу (Эколь Нормал) и начал преподавательскую деятельность. Уже в шестнадцатилетнем возрасте он опубликовал свою первую научную работу. В 1892 г. Жак Адамар стал доктором наук. Адамар страстно любил путешествовать, посетил Китай, Бразилию, США, где читал математические курсы и делал доклады; неоднократно приезжал в СССР. Умер Адамар в октябре 1963 года. 
Большая роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века ^*). Сравнительно недавно, в 1960 г., было замечено, что эти матрицы могут быть использованы для построения кодов с большим кодовым расстоянием



Квадратная матрица Н порядка n с элементами ±1 называется матрицей Адамара, если выполняется условие

НH^T = nЕ_n.

Вот несколько примеров матриц Адамара:

(1),

n = 1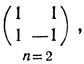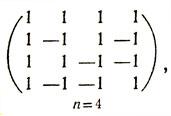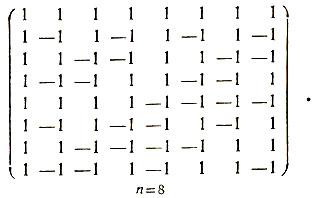







Рассмотрим произвольную матрицу Адамара



h_ij = ± 1.

Из определения следует, что для любой пары строк с номерами i и j (i ≠ j) верно равенство:

h_i1h_j1 + h_i2h_j2 + ... + h_inh_jn = 0. (1)

Таким образом, различные строки матрицы Адамара попарно ортогональны. Далее, число слагаемых в (1), равных +1, должно совпадать с числом слагаемых, равных -1. Следовательно, n четно и любые две строки совпадают ровно в n/2 позициях и различаются в остальных.

^{Построение матриц Адамара}

Если H_n - матрица Адамара порядка n, то легко проверить, что



представляет собой матрицу Адамара порядка 2n. Начав с Н₁= (1), этим методом получаем матрицы Н₂, Н₄, Н₈ и т. д. и, следовательно, матрицы Адамара, порядки которых являются степенями двойки. Эти матрицы Адамара называются матрицами Сильвестра.

Изложим еще один метод построения матрицы Адамара - метод Пэли. Рассмотрим поле Z_р вычетов по модулю р, где р - простое число. Всякий элемент Z_p, являющийся квадратом какого-либо элемента того же поля, называется квадратичным вычетом, всякий другой - квадратичным невычетом. Определим на Z_p следующую функцию χ‾(i), называемую символом Лежандра: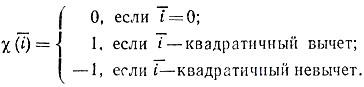



Исходя из этого определения, можно доказать, что для всякого с ≠ 0 выполняется равенство

χ(1‾) χ(‾1 + ‾c) + χ(2‾) χ(‾2 + ‾c) + ... + χ(p-1)‾ χ (p-1‾ + c‾) = -1. (3)

Рассмотрим теперь квадратную матрицу Q порядка р, элементы которой q_ij (i, j = 1, 2, ..., р) определяются следующим образом:

q_ij = χ(j‾ - i‾).

Пусть Е - единичная матрица порядка р, a J - квадратная матрица того же порядка, все элементы которой равны 1. Тогда, пользуясь (3), можно доказать равенства

QQ^T = pE - J, QJ = JQ = 0. (4)

Пусть теперь p = 4k - 1. В этом случае матрица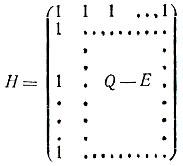



является матрицей Адамара порядка p + 1. Действительно, вычисляя произведение НН^Т, получаем: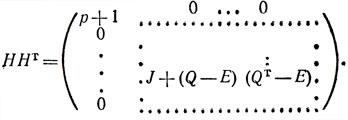



Далее, как нетрудно проверить, матрица Q порядка р = 4k - 1 совпадает с матрицей -Q^T. Отсюда с учетом (4) имеем:

J + (Q - E) (Q^T - E) = J + QQ^T - Q - Q^T + E = J + pE - J - Q + Q + E = (p + 1)E.

Таким образом, HH^T = (р + 1)E.