|
|
Возобновляемые и ресурсосберегающие источники энергии (1). Возобновляемые и ресурсосберегающие источники энергии
Задача 1. Ветроэнергетическая установка при любой скорости ветра поддерживает постоянным коэффициент быстроходности Z = 6. При какой скорости ветра скорость концов лопастей ветроколеса достигнет скорости звука?
Решение
Пусть V – скорость звука. Но V = ZUo, где Uo – скорость ветра,
Z – быстроходность.
Тогда Uo = V/Z = 330/6 = 55 м/с.
Задача 2. Зная, что оптимальная быстроходность ветроколеса определяется соотношением Z = 4π/n, где n-количество лопастей. Вычислить Zo для двухлопастного, трех- и четырехлопастного ветроколеса.
Решение
Zo = 4π/2 6,28
6
Zo = 4π/3= 4,18
4; Zo = 4 π /4 = π
3.
Задача 3. Вычислить скорость ветра на высоте Z = 50 м, если на высоте h = 10 м скорость ветра равна 8 м/с; параметр b = 0,14.
Решение
Для определения скорости ветра на высоте z воспользуемся соотношением
Uz = Us (Z/h)b' (1)
Здесь Us = 8 м/с, Z = 50 м, h = 10 м, b'= 0,14.
Подставив в (1) числовые данные, получим:
Uz = 8 (50/10)0,14= 8 5 0,14 = 8 1,25 = 10,02м/с
10 м/с.
Задача 4. Вычислить диаметр ветроколеса для ВЭУ большой мощности Р=1000 кВт, если плотность воздуха р = 1,2 кг/м3, скорость ветра 8 м/с и Ср = 0,59.
Решение
Расчетная или проектная мощность ВЭУ определяется выражением (3.12) или (3.13) т.е.
Р = 0,5 р А Ср U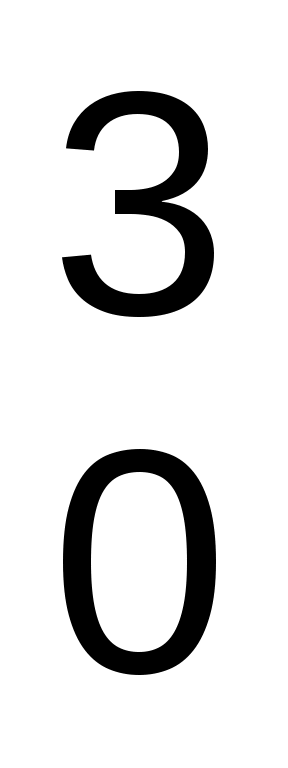 . (2) . (2)
Из (2) имеем
А = Р/0,5р CpU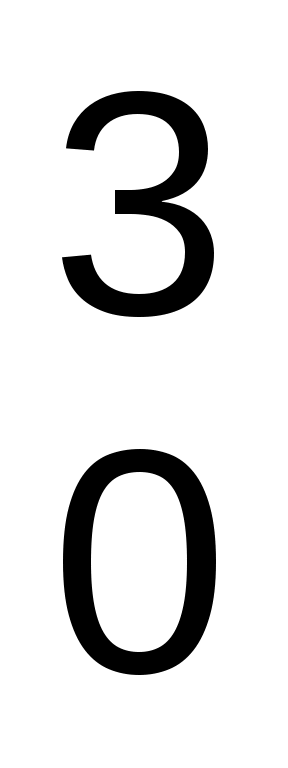 , (3) , (3)
используя выражение А = 0,25 D2, получаем D = 83 м.
5.13. Задачи
1. Какую мощность развивает ветроколесо, если скорость ветра Uo = 10 м/с при плотности воздуха р = 1,29 кг/м3. Площадь, сметаемая ветроколесом А = 5 м2, коэффициент мощности Ср =0,5.
Ответ: Р=1612,5 Вт.
2. Найти коэффициент торможения потока а, если известно что мощность набегающего ветрового потока Ро = 1000 кВт, а мощность передаваемая колесу Р=500 Вт.
Ответ: а = 0,125.
3. Определить радиус ветроколеса при быстроходности Zo = , частоте вращения = 3 Гц и скорости набегающего на лопасть потока Uo = 10 м/с.
Ответ: R= 15 м.
4. Определить мощность Р ВЭС, состоящей из 10 установок при средней скорости ветра V = 10 м/с, если каждое колесо ометает площадь А = 5 м2, а коэффициент мощности Ср = 0,5.
Ответ: Р=16 кВт.
5. Для небольшой станции требуется мощность Р = 10 кВт и известно, что средняя скорость ветра в данном районе V = 10 м/с, какого радиуса R должно быть ветроколесо, чтобы обеспечить эту станцию электроэнергией. Принять, что Ср = 0,5.
Ответ: R = 3,57 м.
6. Для снабжения поселка Березовка (Хабаровский край) электроэнергией требуется мощность Р = 5 МВт. Известно, что площадь, необходимая для установки одного ветряка So = 10 м2, площадь ометаемая этим колесом А = 4,5 м2. Определить площадь, занимаемую для застройки ВЭУ, если известно, что средняя скорость ветра в этом районе Uo = 12 м/с, коэффициент быстроходности
Ср = 0,5 при данной скорости ветра.
Ответ: S = 257200 м2.
7. Сколько лопастей n должно содержать ветроколесо, чтобы достигнуть оптимальную быстроходность при скорости ветра Uo и радиусе ветроколеса R = 1 м, если угловая скорость вращения ветроколеса = 84 Гц.
Ответ: п = 3.
8. Ветроколесо, установленное в Находке, имеет длину лопасти L = 1м, число лопастей на колесе п = 3. При какой скорости ветра Uo колесо будет работать в оптимальном режиме, если оптимальная угловая частота вращения = 54 Гц.
Ответ: Uo = 13 м/с.
9. Определить, на какой высоте hmin от поверхности земли должен находиться центр ветроколеса, если скорость ветра V = 15 м/с, количество лопастей колеса п = 3, и угловая скорость вращения колеса = 6 рад/с.
Ответ: hmin = 10,3м, если ветроколесо перпендикулярно поверхности земли.
10. Какова скорость набегающего потока Uo при максимально лобовой нагрузке, действующей на ветроколесо Fлтах = 600 Н? Плотность воздуха = 1,2 кг/м3, площадь, ометаемая колесом А = 10 м2.
Ответ: Uo = 10 м/с.
11. Определить максимальный крутящий момент Тmах, если радиус ветроколеса R = 3 м, скорость ветра Uo = 15 м/с, плотность воздуха = 1,2 кг/м3, площадь ометаемого потока А = 25 м2.
Ответ: Тmах = 3375 Н.
12. Максимальный крутящий момент ветроколеса Тmах = 600Н, скорость ветра Uo = 10 м/с, плотность воздуха = 1,2кг/м3, площадь, ометаемая ветроколесом А = 6 м2. Найти радиус ветроколеса R и максимальную силу лобового давления на ветроколесо Fлmах, действующего на ветроколесо.
Ответ: R = 1,67 м, Fлmах = 360 Н.
13. Определить коэффициент быстроходности колеса Z, если известна угловая скорость вращения = 3 с-1, скорость потока, набегающего на лопасть Uo = 9 м/с, плотность воздуха, = 1,2кг/м3, ометаемая площадь А = 7 м2, а максимальный крутящий момент Тmах = 700 Н.
Ответ: Z = 0,68.
14. Коэффициент быстроходности ветроколеса Z = 0,5, период за который ветроколесо совершает полный оборот Т = 0,50 с, радиус ветроколеса R = 3 Ом. Определить скорость ветра, набегающего на лопасть.
Ответ: Uo = 19 м/с.
15. Определить плотность воздуха в горах, где установлена ветроустановка, если коэффициент быстроходности колеса Z = 0,5, радиус колеса R = 4 м, угловая скорость вращения = 3 с-1, ометаемая площадь А = 2,5 м2, сила лобового давления на ветроколесо Рлmах = 80 Н.
Ответ: = 1кг/м3.
16. Определить оптимальную быстроходность для трех- и четырехлопастных ветроколес.
Ответ: Для трехлопастного Zо
4,2, для четырехлопастного Zo
.
17. Крупная ВЭУ имеет ветроколесо диаметром 100 м, вращающееся с постоянной угловой скоростью. При какой угловой скорости вращения скорость вращения лопастей достигнет скорости звука?
Ответ: = 6,6 рад/с, = 1,1 Гц.
18. Определить скорость набегающего потока на ветроколеса, если быстроходность данного ветроколеса Z = 7, радиус ветроколеса R = 6 м, угловая скорость вращения = 10 рад/с.
Ответ: Uo = 8,6 м/с.
19. Определить быстроходность ветроколеса, если скорость набегающего потока Uo = 25 м/с, радиус колеса R=10 м, угловая скорость = 5 рад/с.
Ответ: Z = 2.
20. Определить мощность ветроколеса, если мощность набегающего ветрового потока Ро = 1,5 кВт, а коэффициент торможения потока а = 0,2.
Ответ: Р = 768 Вт.
21. Определить мощность ветрового потока, если мощность ветроколеса 2 кВт, а коэффициент торможения потока а = 0,4.
Ответ: Ро = 3,47 кВт.
22. Определить максимальное значение крутящего момента, если скорость ветра 15 м/с, а скорость концов лопастей ветроколеса 45 м/с.
Ответ: (Ст )mах = 0,2.
23. Определить значение оптимальной быстроходности ветроколеса при k = 0,5. Ветроколесо имеет 3 лопасти.
Ответ: Z = 4.
24. Построить график зависимости коэффициента мощности Ср от коэффициента торможения потока а в пределах 0 а 0,5.
25. Определить угловую скорость вращения ВЭУ, если скорость набегающего потока Uo = 16 м/с, а радиус ветроколеса R = 3 м. Коэффициент быстроходности Z = 1.
Ответ: = 5,333 рад/с.
26. Ветроэлектрическая установка при любой скорости ветра поддерживает постоянный коэффициент быстроходности, равный 8. При какой скорости ветра скорость концов лопастей ветроколеса достигнет скорости звука?
Ответ: Uo = 41 м/с.
27. Скорость концов лопастей ВЭУ 200 м/с. Определите угловую скорость вращения, если ветроколесо имеет диаметр 10 м.
Ответ: = 4 рад/с.
28. Определить мощность набегающего потока Ро при скорости ветра Uo = 12 м/с, если мощность ветроколеса Р = 1кВт, ометающего площадь А = 10м2.
Ответ: Ро = 8640 Вт.
29. Какую суммарную площадь ометают ветроколеса установки, развивающей мощность Р=100 кВт при скорости ветра Uo= 17 м/с, Ср = 0,5?
Ответ: А = 81,42 м2.
30. Какова мощность набегающего потока Ро, приходящаяся на 1м2 площади ветроколеса, если самая эффективная установка с диаметром ветроколеса 2,5 м может развить мощность Р = 3 кВт?
Ответ: Ро / ΔS = 1036 Вт/м 2.
31. Постройте зависимость коэффициента быстроходности от числа лопастей и окружной скорости ветроколеса при скорости ветра Uo = 15 м/с.
32. Какова будет скорость ветра, если лобовое давление стало в 2 раза больше, чем лобовое давление при скорости ветра 10 м/с?
Ответ: 14,14 м/с.
33. Определить коэффициент лобового давления трехлопастного ветроколеса, если при скорости ветра 15 м/с лобовое давление на ветроколесо составляло 1200 Н. Площадь, сметаемая ветроколесом, 10 м2.
Ответ: CF= 8/9.
34. Построить зависимость оптимальной скорости ветра от числа
лопастей в колесе при частоте вращения ветроколеса 1 Гц. Радиус
ветроколеса Rk = 1 м.
35. С какой оптимальной частотой должно вращаться ветроколесо радиусом 1 м при скорости ветра 10 м/с и трёх лопастях?
Ответ: = 6,6(6) Гц.
36. Определить частоту вращения колеса турбины , если ее мощность Р = 1 кВт, сила лобового давления на ветроколесо Рлmах = 200 Н и радиус колеса турбины R = 1 м.
Ответ: = 2,5 Гц.
37. Очень часто при оценке ветроэнергетических ресурсов заданного района используют двухпараметрическую функцию распределения Вейбулла для скорости ветра, которая имеет вид
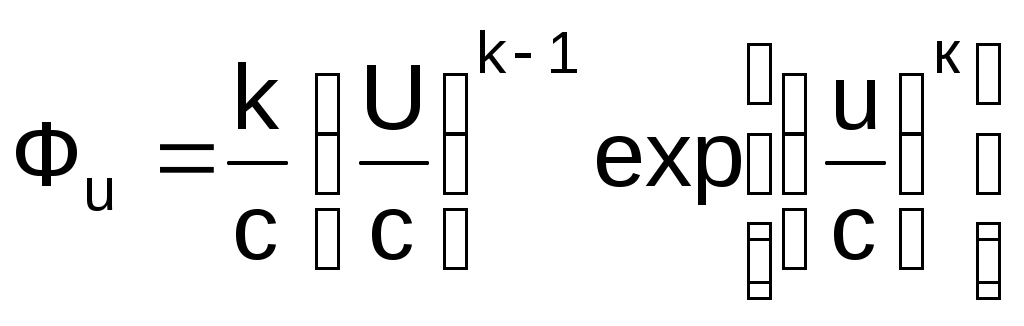 . (4) . (4)
Более точное соответствие экспериментальным результатам получается, если k = 1,8 – 2,3; а параметр с = U, где U – среднее значение скорости ветра в данном регионе.
Фu имеет размерность [м/с]-1. Построить график зависимости Фu =Ф(U) в интервале 1 U 30 м/с через 1 м/с; принять для с = 8,2 м/с. Вычислить скорость, соответствующую максимуму распределения функции скорости ветра Фu. Расчеты сделать на компьютере.
|
|
|
 Скачать 7.49 Mb.
Скачать 7.49 Mb.