курсова. Вступ Розділ I
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
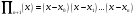 і і 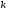 - постійний коефіцієнт, котрий буде обрано нижче. - постійний коефіцієнт, котрий буде обрано нижче.Функція 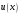 , очевидно, має п+1 корінь в точках , очевидно, має п+1 корінь в точках 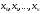 . Підберемо тепер коефіцієнт . Підберемо тепер коефіцієнт 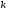 таким чином, щоб таким чином, щоб 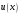 мала (п+2)-ий корінь в будь-якій, але фіксованій точці відрізка мала (п+2)-ий корінь в будь-якій, але фіксованій точці відрізка 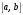 , яка не співпадає з вузлами інтерполювання (мал. 1). Для цього достатньо покласти , яка не співпадає з вузлами інтерполювання (мал. 1). Для цього достатньо покласти 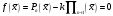 . .Звідси, так як 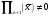 , то , то 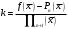 (1. 2. 13) (1. 2. 13)При цьому значення множника 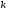 функції функції 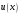 має п+2 кореня на відрізку має п+2 кореня на відрізку 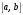 і буде обертатись в нуль на кінцях кожного з відрізків і буде обертатись в нуль на кінцях кожного з відрізків 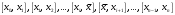 . Застосовуючи теорему Ролля [11] до кожного із цих відрізків, переконуємось, що похідна . Застосовуючи теорему Ролля [11] до кожного із цих відрізків, переконуємось, що похідна 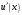 має не менше п+1 кореня на відрізку має не менше п+1 кореня на відрізку 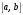 . .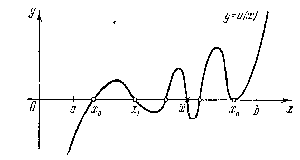 Малюнок 1. Графік функції 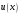 Застосовуючи теорему Ролля до похідної 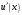 , ми переконаємося, що друга похідна , ми переконаємося, що друга похідна 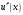 перетворюється в нуль не менше п разів на відрізку перетворюється в нуль не менше п разів на відрізку 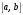 . .Продовжуючи ці роздуми, прийдемо до висновку, що на відрізку 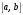 похідна похідна 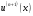 має хоча б один корінь, котрий позначимо через має хоча б один корінь, котрий позначимо через 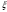 , тобто , тобто 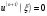 . .Із формули (1. 2. 11) так як 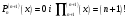 , маємо: , маємо: 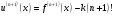 . При . При 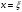 , отримуємо: , отримуємо: 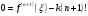 Звідси Звідси 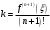 . (1. 2. 14) . (1. 2. 14)Порівнюючи праві частини формул (1. 2. 13) і (1. 2. 14), будемо мати: 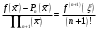 , тобто , тобто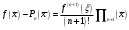 . (1. 2. 15) . (1. 2. 15)Так як 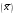 довільне, то формулу (1. 2. 15) можна записати і так: довільне, то формулу (1. 2. 15) можна записати і так: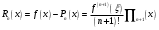 , (1. 2. 16) , (1. 2. 16)де 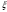 залежить від залежить від  і лежить всередині відрізка і лежить всередині відрізка 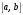 . . Відмітимо, що формула (1. 2. 16) справедлива для всіх точок відрізка 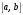 , в тому числі і для вузлів інтерполювання. , в тому числі і для вузлів інтерполювання.На основі формули (1. 2. 16) отримаємо залишковий член першої інтерполяційної формули Ньютона: 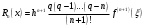 , (1. 2. 17) , (1. 2. 17)де 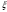 - деяка внутрішня точка найменшого проміжку, що містить всі вузли - деяка внутрішня точка найменшого проміжку, що містить всі вузли 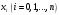 і точку і точку  . .Аналогічно, покладаючи в формулі (1. 2. 17) 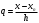 , отримаємо залишковий член другої інтерполяційної формули Ньютона: , отримаємо залишковий член другої інтерполяційної формули Ньютона: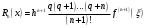 , (1. 2. 18) , (1. 2. 18)де 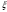 - деяка внутрішня точка найменшого проміжку, що містить всі вузли - деяка внутрішня точка найменшого проміжку, що містить всі вузли 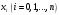 і точку і точку  . . Зазвичай при практичних обчисленнях інтерполяційна формула Ньютона обривається на членах, що містять такі різниці, які в межах заданої точності можна вважати постійними. Вважаючи, що 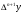 майже постійними для функції майже постійними для функції 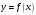 і і 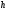 достатньо малим, і враховуючи, що достатньо малим, і враховуючи, що 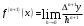 , наближено можна покласти: , наближено можна покласти: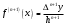 . .В цьому випадку залишковий член першої інтерполяційної формули Ньютона наближено рівний 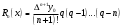 . .При таких самих умовах для залишкового члена другої інтерполяційної формули Ньютона отримаємо вираз 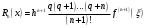 . .1.3 Інтерполяційні формули Гауса При побудові інтерполяційних формул Ньютона використовуються лише значення функції, що лежать з однієї сторони початкового наближення, тобто, ці формули носять односторонній характер (див.[3]). В багатьох випадках виявляються корисними інтерполяційні формули, що містять як наступні, так і попередні значення функції по відношенню до її початкового наближеного значення. Найбільш вживаними серед них являються ті, що містять різниці, розміщені у горизонтальному рядку діагональної таблиці різниць даної функції, що відповідає початковим значенням 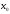 і і 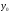 , або в рядках, що безпосередньо примикають до неї. Ці різниці , або в рядках, що безпосередньо примикають до неї. Ці різниці 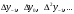 називаються центральними різницями, причому називаються центральними різницями, причому 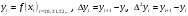 і т. д. і т. д.Відповідні їм формули називають інтерполяційними формулами із центральними різницями. До їх числа відносяться формули Гауса, Стірлінга і Бесселя. Постановка задачі. Нехай маємо 2п+1 рівновіддалені вузли інтерполяції: 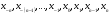 , ,де 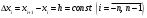 , і для функції , і для функції 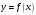 відомі її значення в цих вузлах відомі її значення в цих вузлах 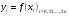 , потрібно побудувати такий поліном , потрібно побудувати такий поліном 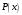 степені не вище 2п, що степені не вище 2п, що 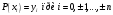 . Із останньої умови випливає, що . Із останньої умови випливає, що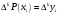 (1. 3. 1) (1. 3. 1)для всіх відповідних значень і та k. Будемо шукати поліном у вигляді: 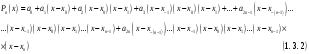 Вводячи узагальнені степені (див [3]), отримаємо: 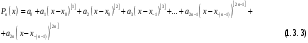 Застосовуючи для обчислення коефіцієнтів 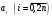 такий же спосіб, що і при виведенні інтерполяційних формул Ньютона, і враховуючи формулу (1. 3. 1), послідовно знаходимо: такий же спосіб, що і при виведенні інтерполяційних формул Ньютона, і враховуючи формулу (1. 3. 1), послідовно знаходимо: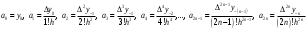 Далі вводячи змінну 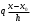 і зробивши відповідну заміну у формулі (1. 3. 3), отримаємо першу інтерполяційну формулу Гауса: і зробивши відповідну заміну у формулі (1. 3. 3), отримаємо першу інтерполяційну формулу Гауса: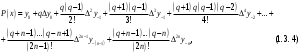 або, коротше, 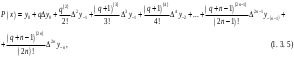 де 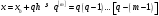 . .Перша інтерполяційна формула Гауса містить центральні різниці 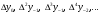 . .Аналогічно можна отримати другу інтерполяційну формулу Гауса, котра містить центральні різниці 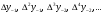 . Друга інтерполяційна формула Гауса має вигляд: . Друга інтерполяційна формула Гауса має вигляд: 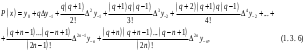 або, в скорочених позначеннях, 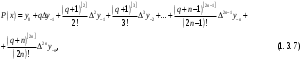 де 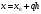 . .Формули Гауса застосовуються для інтерполювання в середині таблиці поблизу 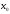 . При цьому перша формула Гауса застосовується при . При цьому перша формула Гауса застосовується при 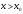 , а друга – при , а друга – при 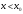 . .1.4 Інтерполяційна формула Бесселя Для того, щоб вивести формулу Бесселя використаємо другу інтерполяційну формулу Гауса (1. 3. 6). Візьмемо 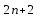 рівновіддалених вузлів інтерполювання рівновіддалених вузлів інтерполювання 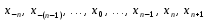 з кроком з кроком 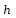 , і нехай , і нехай 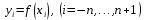 - задані значення функції - задані значення функції 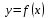 . .Якщо обрати за початкове значення 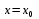 і і 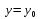 , то, використовуючи вузли , то, використовуючи вузли 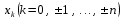 , будемо мати: , будемо мати: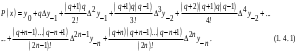 прикладний задача інтерполяційний формула Візьмемо тепер за початкове значення 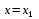 і і 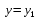 і використаємо вузли і використаємо вузли 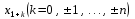 . Тоді . Тоді 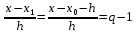 , причому відповідно індекси всіх різниць в правій частині формули (1. 4. 1) зростуть на одиницю. Якщо замінити в правій частині формули (1. 4. 1) , причому відповідно індекси всіх різниць в правій частині формули (1. 4. 1) зростуть на одиницю. Якщо замінити в правій частині формули (1. 4. 1) 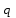 на на 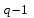 і збільшивши індекси всіх різниць на 1, отримаємо допоміжну інтерполяційну формулу: і збільшивши індекси всіх різниць на 1, отримаємо допоміжну інтерполяційну формулу: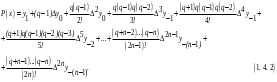 Взявши середнє арифметичне формул (1. 4. 1) і (1. 4. 2), після нескладних перетворень отримаємо інтерполяційну формулу Бесселя:  де 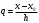 . .Тобто, інтерполяційна формула Бесселя (1. 4. 3), як слідує із способу отримання її, представляє собою поліном, який співпадає з даною функцією 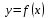 в в 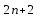 точках точках 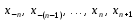 . .В окремому випадку, при п=1, нехтуючи різницею 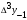 , маємо формулу квадратичної інтерполяції по Бесселю: , маємо формулу квадратичної інтерполяції по Бесселю: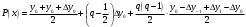 або 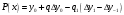 , де , де 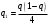 . .У формулі Бесселя всі члени, котрі містять різниці непарного порядку, мають множник 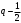 , тому при , тому при 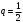 формула (1. 4. 3) значно спрощується: формула (1. 4. 3) значно спрощується: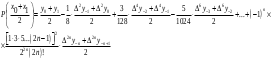 Цей спеціальний випадок формули Бесселя називається формулою інтерполювання на середину. Якщо у формулі (1. 4. 3) зробити заміну змінної за формулою 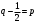 , то вона приймає більш симетричний вигляд: , то вона приймає більш симетричний вигляд: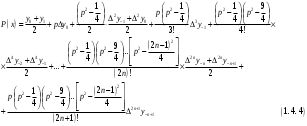 де 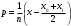 . . Формула Бесселя використовується для інтерполювання всередині таблиці при значеннях q, близьких до 0.5. Практично вона використовується при 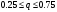 . . 1.5 Інтерполяційна формула Стірлінга Якщо взяти середнє арифметичне першої інтерполяційної формули Гауса (1. 3. 4) та другої формули Гауса (1. 3. 6), то отримаємо формулу Стірлінга: 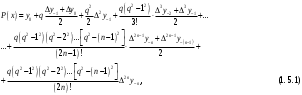 де 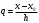 . .Легко бачити, що 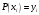 при при 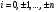 . . Формула Стірлінга використовується для інтерполювання в середині таблиці при значеннях 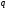 , близьких до нуля. Практично її використовують при , близьких до нуля. Практично її використовують при 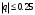 . .1.6 Оцінки похибок центральних інтерполяційних формул Приведемо залишкові члени для формул Гауса, Стірлінга і Бесселя [12]. Залишковий член інтерполяційних формул Гауса (1. 3. 4) і (1. 3. 6) та інтерполяційної формули Стірлінга (1. 5. 1). Якщо 2п – порядок максимальної різниці таблиці, яка використовується і 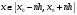 , то , то 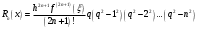 , , де 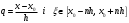 . . Якщо ж аналітичний вираз функції 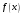 невідомий, то при невідомий, то при 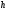 малому покладають [2]: малому покладають [2]: 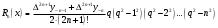 . .Залишковий член інтерполяційної формули Бесселя (1. 4. 3). Якщо 2п+1 – порядок максимальної використовуваної різниці таблиці і 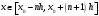 , то , то 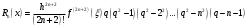 , ,де 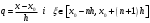 . . Якщо ж функція 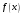 задана таблично і крок h малий, то приймають: задана таблично і крок h малий, то приймають: 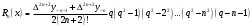 . .Найбільш простий вигляд формула має при q=0.5, так як всі члени, що містять різниці непарного порядку зникають. Цей спеціальний випадок формули Бесселя називається формулою інтерполювання на середину. Її використовують для ущільнення таблиць [4], тобто для складання таблиць з більш малим кроком. Для залишкового члена при q=0.5 маємо: 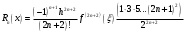 . .1.7 Інтерполяційна формула Ньютона для нерівновіддалених вузлів Для побудови інтерполяційних формул у випадку довільного розташування упорядкованих не співпадаючих вузлів 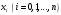 на проміжку на проміжку 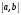 , замість кінцевих різниць використовують розділені різниці, або інакше, різницеві відношення. , замість кінцевих різниць використовують розділені різниці, або інакше, різницеві відношення.Через значення функції 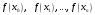 спочатку визначають розділені різниці першого порядку: спочатку визначають розділені різниці першого порядку: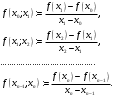 (1. 7. 1) (1. 7. 1)На різницях (1. 7. 1) шукаються розділені різниці другого порядку: 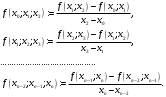 і т.д. Таким чином, якщо визначені k-ті різницеві відношення 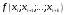 , то , то 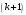 - ті визначаються завдяки ним рівністю: - ті визначаються завдяки ним рівністю: 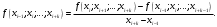 (1. 7. 2) (1. 7. 2) Нехай 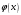 - деяка функція із відомими значеннями у вузлах - деяка функція із відомими значеннями у вузлах 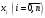 , а , а  - довільна фіксована точка. За означенням розділеної різниці першого порядку (1. 7. 1) маємо: - довільна фіксована точка. За означенням розділеної різниці першого порядку (1. 7. 1) маємо: 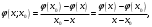 звідки звідки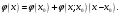 (1. 7. 3) (1. 7. 3)Для розділеної різниці другого порядку по точкам 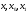 записуємо представлення: записуємо представлення: 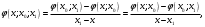 наслідком якого являється вираз наслідком якого являється вираз 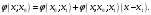 Підставляючи його у формулу (1. 7. 2), приходимо до рівності Підставляючи його у формулу (1. 7. 2), приходимо до рівності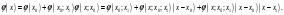 Формально, на основі рекурентного відношення (1. 7. 2) цей процес може бути продовжений. В результаті можна записати формулу, яка описує своєрідне розкладання 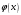 по добуткам різниць по добуткам різниць 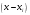 , коефіцієнтами якого являються розділені різниці різних порядків: , коефіцієнтами якого являються розділені різниці різних порядків: 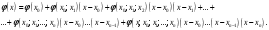 (1. 7. 4) (1. 7. 4)Якщо 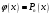 - многочлен степені п, то процес подібного розкладання вичерпується. Розкладання буде складатись з п+1 доданка, і всі вони будуть мати конкретні коефіцієнти, так як остання, яка містить - многочлен степені п, то процес подібного розкладання вичерпується. Розкладання буде складатись з п+1 доданка, і всі вони будуть мати конкретні коефіцієнти, так як остання, яка містить |
