курсова. Вступ Розділ I
 Скачать 0.94 Mb.
|
 відповідно до формул, які застосовуються, тобто тут також використовується функція DeltaCount;PaintPlot – функція для побудови графіку. В даному випадку сам графік будується в електронній таблиці Excel, результат імпортується в С# і відбувається вивід у вікно програми; WhereIsX – функція, яка визначає, де знаходиться х у таблиці кінцевих різниць (ближче до початку, кінця чи до середени) і відповідно до того як написано вище в теоретичній частині у випадку, коли користувач забуде обрати формулу для обчислень, сама обирає, яку формулу краще застосовувати; Тобто це основні функції та процедури, окрім них в програмі ще використовуються допоміжні функції для зчитування даних, для перевірки правильності введених даних, для зберігання результатів у файл, для запуску тестового прикладу, який розглядався в пункті 1.8.1 і т.д. 1.9.3 Інструкція по використанню програми Для запуску програми «InterPolation» потрібно відкрити папку Release і запустити InterPolation.ехе. В результаті з’явиться вікно програми (мал. 2). 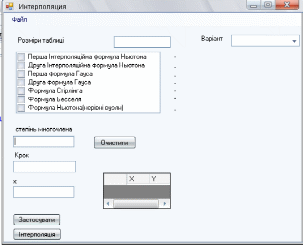 Мал. 2. Інтерфейс основної форми програми У полі «х» вводиться значення аргументу, для якого необхідно наближено обчислити значення функції, заданої відповідною таблицею. У полі «степінь многочлена» користувачеві необхідно ввести степінь многочленна для наближення функції. У поле «крок» потрібно ввести крок h, а в полі «Розміри таблиці» вводиться кількість даних фіксованих значень функції. Потім у відповідному віконці обирається формула, яка застосовується для наближення. Після цього натискаємо кнопку «Застосувати» і у вікні ще з’являється табличка для вводу хі, уі. Після заповнення таблиці потрібно натиснути кнопку «Інтерполяція» для того, щоб програма виконала необхідні обчислення і видала результат. Крім того, з правого боку є випадаючий список «Варіант», де користувач може обрати один із 30-ти варіантів вихідних даних, що містяться в [7], потім знову ж таки обрати степінь полінома, х, формули, які хоче застосовувати. В меню «Файл» користувач може обрати «Тестовий варіант». В результаті програма виведе всі результати обчислень згідно прикладу 1 (пункт 1.8.1) (мал. 3): 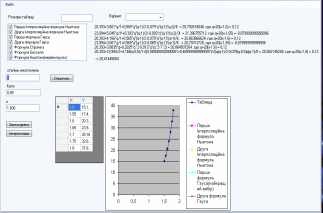 Мал. 3. Тестовий варіант В меню файл користувач також може обрати «Зберегти». В результаті програма збереже результати роботи програми у файл. Тип файлу визначає сам користувач. Тобто, якщо, наприклад, зберегти результати обчислень тестового варіанту у текстовому документі, то відкривши цей файл будемо мати наступне (мал. 4):  Мал. 4. Лістинг результатів 1.9.4 Перевірка працездатності програми Покажемо працездатність програми на прикладі 1 (пункт 1.8.1). Для цього можна самостійно ввести всі необхідні дані або обрати в меню файл, як зазначалося вище, пункт «тестовий варіант». Як видно з результатів, отриманих при застосуванні програми (мал. 3), всі формули дають майже однакове наближення, окрім формули Бесселя (дану формулу краще використовувати при 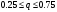 ). Особливо добре це видно з графіка. Тепер порівняємо отриманий результат із розрахунками, отриманими за допомогою електронної таблиці Excel (див. мал. 5).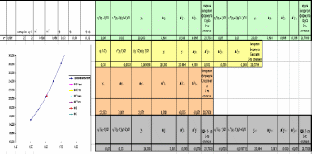 Мал. 5. Результати обчислень в електронній таблиці Excel Тобто бачимо, що отримані результати дещо відрізняються (на 0,01). Це пов’язано з тим, що в електронній таблиці менша точність обчислень, ніж у програмі. Однак, збільшуючи степінь полінома отримаємо практично однакові результати. Код програми в додатку 1. Література Ильин В.А., Позняк Э. Г., Основы математического анализа, ч. II.- М.: Наука, 1980, с.50 Демидович Б. П., Марон И. А., Основы вычеслительной математики, Наука, 1970. http://miest.narod.ru Копченова Н.В., Марон И.А. – Вычислительная математика в примерах и задачах. «Наука» Москва, 1972г. Турчак Л.И. – Основы численных методов. «Наука» Москва, 1987г. Вержбицкий В. М., Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. «Высшая школа» Москва, 2001 Воробьева Г. Н., Данилова А. Н. Практикум по вычислительной матиматике, изд.-II, «Высшая школа», Москва, 1990 Калиткин Н. П., Численные методы. - М.: Наука, 1978 Полия Г., Сеге Г. Теория функций (специальная часть).- М., 1978 Буслов В.А., Яковлев С.Л. Численные методы ІІ. Решение уравнений. Курс лекций. Санкт-Петербург, 2001 Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. - Численные методы, М., Наука, 1987 Хаусхолдер А. С., Основы численного анализа.-М., 1953 |