курсова. Вступ Розділ I
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
 , розділена різниця в (1. 7. 4), тобто , розділена різниця в (1. 7. 4), тобто 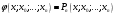 має (п+1)-ий порядок і, значить, дорівнює нулю. Таким чином, для довільного многочленна степені п справедлива тотожність має (п+1)-ий порядок і, значить, дорівнює нулю. Таким чином, для довільного многочленна степені п справедлива тотожність 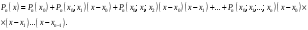 Припустимо, що цей многочлен 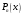 являється інтерполяційним для деякої функції являється інтерполяційним для деякої функції 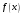 . Тоді у всіх вузлах . Тоді у всіх вузлах 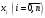 він повинен мати однакові з нею значення, а отже повинні бути однаковими і їх розділені різниці. Звідси приходимо до інтерполяційної формули Ньютона для нерівновіддалених вузлів: він повинен мати однакові з нею значення, а отже повинні бути однаковими і їх розділені різниці. Звідси приходимо до інтерполяційної формули Ньютона для нерівновіддалених вузлів: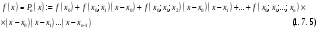 Підставивши 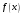 замість замість 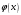 у формулу (1. 7. 4), з урахуванням (1. 7. 5) отримуємо точну рівність у формулу (1. 7. 4), з урахуванням (1. 7. 5) отримуємо точну рівність 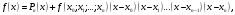 другий доданок якої може розглядатись в якості залишкового члена, тобто 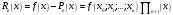 , (1. 7. 6) , (1. 7. 6)де 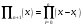 . .Так як для обчислення різниці 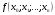 необхідно знання значення необхідно знання значення 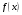 поряд з відомими значеннями поряд з відомими значеннями 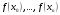 , представлений формулою (1. 7. 5) вираз , представлений формулою (1. 7. 5) вираз 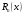 фактично можна використовувати тільки для оцінювання похибки інтерполювання за формулою (1. 7. 5) через максимальні величини модулів розділених різниць (п+1)-го порядку або для одержання інших виразів залишкового члена при тих чи інших припущеннях про дану функцію. Зокрема, якщо функція фактично можна використовувати тільки для оцінювання похибки інтерполювання за формулою (1. 7. 5) через максимальні величини модулів розділених різниць (п+1)-го порядку або для одержання інших виразів залишкового члена при тих чи інших припущеннях про дану функцію. Зокрема, якщо функція 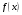 має (п+1)-шу похідну, то залишковий член (1. 7. 6) може бути приведений до вигляду має (п+1)-шу похідну, то залишковий член (1. 7. 6) може бути приведений до вигляду 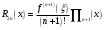 . .При практичному використання інтерполяційної формули (1. 7. 5) доводиться покладатися на зменшення модулів доданків 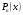 при збільшенні номера доданка. Таке зменшення відбувається до деяких пір; потім починається зростання їх модулів із-за впливу похибок заокруглення. при збільшенні номера доданка. Таке зменшення відбувається до деяких пір; потім починається зростання їх модулів із-за впливу похибок заокруглення.1.8 Приклади застосування інтерполяційних формул 1.8.1 Приклад 1 Використовуючи першу і другу інтерполяційну формулу Ньютона і Гауса, а також інтерполяційні формули Стірлінга і Бесселя необхідно знайти значення функції 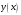 , заданої таблицею (табл. 1) при значенні аргументу , заданої таблицею (табл. 1) при значенні аргументу 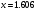 . При цьому крок . При цьому крок 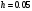 . . Таблиця 1. Значення функції
Розв’язання: Складемо спочатку таблицю кінцевих різниць (табл. 2). Таблиця 2. Кінцеві різниці
При складанні таблиці різниць обмежимося різницями третього порядку, оскільки вони практично постійні. За першою інтерполяційною формулою Ньютона (1. 2. 7), приймаючи 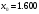 , , 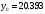 (табл. 2), отримаємо: (табл. 2), отримаємо: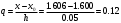 ; ; 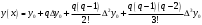 ; ;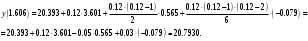 За другою інтерполяційною формулою Ньютона (1. 2. 11), приймаючи 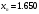 , , 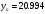 (табл. 2), отримаємо: (табл. 2), отримаємо: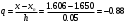 ; ;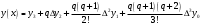 ; ;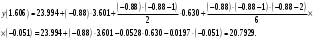 За першою інтерполяційною формулою Гауса (1. 3. 4), приймаючи 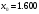 , , 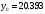 , матимемо: , матимемо: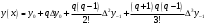 . .Отже, отримаємо: 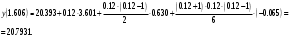 За другою інтерполяційною формулою Гауса (1. 3. 6), приймаючи 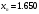 , , 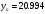 , отримаємо: , отримаємо: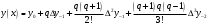 ; ;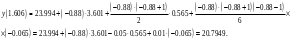 За інтерполяційною формулою Стірлінга, підставляючи відповідні коефіцієнти із таблиці різниць (табл. 2) у формулу (1. 5. 1) отримаємо: 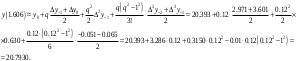 За інтерполяційною формулою Бесселя, підставляючи відповідні коефіцієнти із таблиці різниць (табл. 2) в формулу (1. 4. 3) отримаємо: 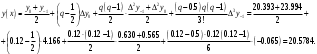 Тепер проведемо оцінку отриманих результатів. Введемо наступні позначення: ІФН – інтерполяційна формула Ньютона; ІФГ - інтерполяційна формула Гауса; ІФБ - інтерполяційна формула Бесселя; ІФС - інтерполяційна формула Стірлінга. Для зручності результати запишемо у вигляді таблиці (табл. 3):
Таблиця 3. Отримані результати. Тепер визначимо похибку отриманих результатів. Для цього від значення, отриманого за допомогою першої ІФН, віднімемо результати, отримані зі допомогою інших формул. В результаті отримаємо таку розрахункову табличку (табл. 4):
Таблиця 4. Абсолютні похибки результатів. Тоді, щоб отримати відносну похибку результату, необхідно абсолютні похибки поділити на відповідні отримані наближені значення 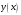 , отримані за формулами (1. 2. 7), (1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1). Тобто маємо (табл. 5): , отримані за формулами (1. 2. 7), (1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1). Тобто маємо (табл. 5):
Таблиця 5. Відносні похибки. Бачимо, найкраще наближення до значення, одержаного за ІФН 1-ою, досягається інтерполяційною формулою Стірлінга. Висновок. Як зазначалося вище (див. пункт 1.6), ІФС краще використовувати, для інтерполювання в середині таблиці, в чому ми і переконалися в даному прикладі, оскільки 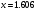 знаходиться всередині таблиці. знаходиться всередині таблиці.1.8.2 Приклад 2 Знайти значення функції 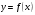 , заданої таблицею (табл. 6) при значенню аргументу , заданої таблицею (табл. 6) при значенню аргументу 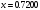 , використовуючи інтерполяційну формулу Ньютона для нерівновіддалених вузлів. При розрахунках враховувати лише розділені різниці першого і другого порядків. , використовуючи інтерполяційну формулу Ньютона для нерівновіддалених вузлів. При розрахунках враховувати лише розділені різниці першого і другого порядків. Таблиця 6. Значення функції
Розв’язання: Оскільки в умові сказано використовувати лише розділені різниці другого і третього порядку, то формула Ньютона для нерівновіддалених вузлів (1. 7. 5) матиме вигляд: 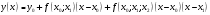 , , де 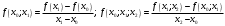 . .Попередньо обчислимо необхідні значення розділених різниць (табл. 7). Таблиця 7. Розділені різниці
Для визначення  приймаємо приймаємо 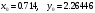 . Для зручності складаємо допоміжну розрахункову таблицю (табл. 8), звідки отримаємо: . Для зручності складаємо допоміжну розрахункову таблицю (табл. 8), звідки отримаємо: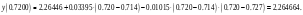 Таблиця 8. Розрахункова таблиця  1.9 Програмна реалізація 1.9.1 Призначення програми Дану програму було розроблено з метою надання можливості за допомогою ЕОМ обчислювати наближені значення функції у випадку, коли функція задана таблично, використовуючи для цього інтерполяційні формули для рівновіддалених вузлів (1. 2. 7), (1. 2. 11), (1. 3. 4), (1. 3. 6), (1. 4. 3), (1. 5. 1) та інтерполяційну формулу (1. 7. 5)- для нерівновіддалених вузлів. Крім того, враховано можливість отримання загального вигляду відповідного інтерполяційного поліному наближення з метою подальшого використання при, наприклад, плануванні експериментів в біології, фізиці, хімії, географії, медицині та ін. галузях науки. Так як програма, більшою мірою, призначення для використання в навчальних цілях, то в ній передбачена можливість вибору початкових даних згідно варінтів лабораторних робіт, наведених в [7], що дає можливість зменшити витрати часу при введені даних для студентів. 1.9.2 Основні процедури Програмну реалізацію було здійснено в інтегрованому середовищі розробки Microsoft Visual Studio 2008 Team System у проекті типу Visual C# з використанням мови програмування С# на базі технології .NET Framework 2.0. Програма має назву «InterPolation». Розглянемо основні процедури і функції програми та їх призначення: DeltaCount – функція для побудови таблиці кінцевих різниць по заданим данним (вхідними даними є введені користувачем значення функції типу double); Fact – функція для обчислення факторіалів, необхідних для застосування формул (5), (9), (12), (13), (15), (16). Вхідними даними для цієї функції слугує степінь полінома n, введеного користувачем, яка має тип integer; EvalNewtonNerivni – функція, яка перевіряє, чи вузли інтерполяції є рівновіддаленими, чи нерівновіддаленим. У випадку нерівновіддалених вузлів обчислює наближене значення функції за формулою (20). Дана функція використовує вже написану функцію DeltaCount, для отримання необхідних для формули данних. EvalFFNewton – функція, яка застосовує першу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи функцію DeltaCount та функцію Fact. Результатом її виконання буде наближене значення функції згідно формули (5) типу double; FFNewton – функція, що виводить формулу (5) і обчислене згідно функції EvalFFNewton наближення функції; EvalSFNewton - функція, яка застосовує другу інтерполяційну формулу Ньютона згідно з введеними даними і використовуючи функцію DeltaCount та функцію Fact. Результатом її виконання буде наближене значення функції згідно формули (9) типу double; FFNewton – функція, що виводить формулу (9) і обчислене згідно функції EvalSFNewton наближення функції; Аналогіно відповідно працють функції EvalFFGauss і FFGauss для першої формули Гауса, EvalSFGauss і SFGauss для другої формули Гауса, EvalFStirling і FStirling для формули Стірлінга та EvalFBessel і FBessel для формули Бесселя. GetX0 – функція для визначення умовного нуля |
