курсова. Вступ Розділ I
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
Зміст ВступРозділ IІнтерполювання функцій1.1 Постановка задачі1.2 Інтерполяційні формули Ньютона1.2.1 Перша інтерполяційна формула Ньютона1.2.2 Друга інтерполяційна формула Ньютона1.2.3 Оцінка похибок інтерполяційних формул Ньютона1.3 Інтерполяційні формули Гауса1.4 Інтерполяційна формула Бесселя1.5 Інтерполяційна формула Стірлінга1.6 Оцінки похибок центральних інтерполяційних формул1.7 Інтерполяційна формула Ньютона для нерівновіддалених вузлів1.8 Приклади застосування інтерполяційних формул1.8.1 Приклад 11.8.2 Приклад 21.9 Програмна реалізація1.9.1 Призначення програми1.9.2 Основні процедури1.9.3 Інструкція по використанню програми1.9.4 Перевірка працездатності програмиРозділ ІІЛітератураДодаткиВступ У зв’язку з розвитком обчислювальної техніки інженерна практика наших днів все частіше і частіше зустрічається з математичними задачами, точний розв’язок яких отримати достатньо важко. В таких випадках зазвичай звертаються до тих чи інших наближених обчислень. Ось чому наближені і чисельні методи математичного аналізу отримали за останні роки широкий розвиток і набули виключно важливого значення. Чисельне розв’язання прикладних задач завжди цікавило математиків. Аналіз ускладнених моделей вимагав створення спеціальних, як правило, чисельних або асимптотичних методів розв’язання завдань. Назви деяких з таких методів - методи Ньютона, Ейлера, Лобачевського, Гауса, Чебишева, Ерміта, Крилова - свідчать про те, що їх розробкою займалися найвидатніші вчені свого часу. Чисельні методи є одним з могутніх математичних засобів розв’язання задач. Прості чисельні методи ми використовуємо скрізь, наприклад, при знаходженні квадратного кореня на листку паперу. Є завдання, де без достатньо складних чисельних методів не вдалося б отримати відповіді. Класичний приклад — відкриття Нептуна по аномаліях руху Урану. Загалом у курсах чисельних методів вивчаються питання побудови, застосування і теоретичного обґрунтування алгоритмів наближеного розв’язання різних класів математичних задач. У наш час більшість обчислювальних алгоритмів орієнтовано на використання швидкодіючих ЕОМ, що значно впливає на підбір учбового матеріалу й на характер його викладу. Тільки обчислювальній машині під силу виконувати за короткий час об'єм обчислень в мільярди, трильйони і більше операції, які необхідні для вирішення багатьох сучасних завдань. Варто відмітити деякі особливості предмету чисельних методів. По-перше, для чисельних методів характерна множинність, тобто можливість розв’язати одну й ту саму задачу різними методами. По-друге, природничонаукові задачі і швидкий розвиток обчислювальної техніки змушують переоцінювати значення існуючих алгоритмів і призводять до створення нових. По-третє, чисельні методи разом із можливістю отримання результату за прийнятний час не повинні вносити у обчислювальний процес значних похибок. У даній курсовій роботі розглядається задача про інтерполяцію функції. Якщо задана функція y(x), то це означає, що будь-якому допустимому значенню х ставиться у відповідність значення у. Однак, нерідко виявляється, що знаходження цього значення дуже трудомістке. Наприклад, у(х) може бути визначене як розв’язок складної задачі, в якій х виконує роль параметра, або у(х) вимірюється в дорогому експерименті. При цьому можна обчислити невелику таблицю значень функції, але пряме знаходження функції при великому числі значень аргументу буде практично неможливо. Функція у(х) може брати участь у будь-яких фізико-технічних або чисто математичних розрахунках, де її доводиться багато разів обчислювати. У цьому випадку вигідно замінити функцію у (х) наближеною відомою функцією, тобто підібрати деяку функцію f(x), яка близька у певному сенсі до у(х) і легко обчислюється. Потім при всіх значеннях аргументу вважають, що 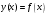 . .Більша частина класичного чисельного аналізу ґрунтується на наближенні многочленами, оскільки з ними легко працювати. Однак для багатьох цілей використовують і інші класи функцій (див. [2]). Вибравши вузлові точки і клас функцій, що наближають, ми повинні також вибрати одну певну функцію з цього класу за допомогою деякого критерію - міри наближення або «згоди». Перш, ніж почати обчислення, ми повинні вирішити також, яку точність ми хочемо мати у відповіді і який критерій ми оберемо для вимірювання цієї точності. Все викладене можна сформулювати у вигляді чотирьох питань: Які вузли ми будемо використовувати? Який клас функцій для наближення будемо використовувати? Який критерій згоди ми застосуємо? Яку точність ми хочемо? Існує 3 класи або групи функцій, широко застосовуваних у чисельному аналізі. Перша група включає в себе лінійні комбінації функцій 1, х, х2, ..., хn, що збігається з класом усіх многочленів степені n (або менше). Другий клас утворюють функції cos aix, sin aix. Цей клас має відношення до рядів Фур'є та інтегралу Фур'є. Третя група утворюється функціями e-az. Ці функції зустрічаються в реальних ситуаціях. До них, наприклад, призводять задачі накопичення і розпаду. Що стосується критерію згоди, то класичним критерієм згоди є «точний збіг у вузлових точках». Цей критерій має перевагу завдяки простоті теорії та виконанню обчислень, але також незручність через ігнорування похибки (шуму), що виникає при вимірюванні або обчисленні значень у вузлових точках. Інший відносно хороший критерій - це «найменші квадрати». Він означає, що сума квадратів відхилень у вузлових точках повинна бути найменшою можливою або, іншими словами, мінімізована. Цей критерій використовує помилкову інформацію, щоб отримати деяке згладжування шуму. Третій критерій пов’язаний з ім'ям Чебишева. Основна ідея його полягає в тому, щоб зменшити максимальне відхилення до мінімуму. Очевидно, можливі й інші критерії. Більш конкретно відповісти на поставлені 4 питання можна лише виходячи з умов і мети кожної окремої задачі. Розділ I. Інтерполювання функцій 1.1 Постановка задачі Однією з основних задач чисельного аналізу являється задача про інтерполяцію функції. Багатьом з тих, хто стикається з науковими та інженерними розрахунками часто доводиться оперувати наборами значень, отриманих експериментальним шляхом чи методом випадкової вибірки. Як правило, на підставі цих наборів потрібно побудувати функцію, зі значеннями якої могли б з високою точністю збігатися інші отримувані значення. Така задача називається апроксимацією кривої. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних. Існує також близька до інтерполяції задача, що полягає в апроксимації якої-небудь складної функції іншою, більш простою функцією. Якщо деяка функція занадто складна для продуктивних обчислень, можна спробувати обчислити її значення в декількох точках, а по них побудувати, тобто інтерполювати, більш просту функцію. Зрозуміло, використання спрощеної функції не дозволяє одержати такі ж точні результати, які давала б початкова функція. Але, для деяких класів задач, досягнутий виграш у простоті і швидкості обчислень може переважити отриману похибку у результатах. Варто також згадати і зовсім інший різновид математичної інтерполяції, відому за назвою «інтерполяція операторів». До класичних робіт по інтерполяції операторів відносяться теорема Ріса-Торина і теорема Марцинкевича (див. [3]), що є основою для багатьох інших робіт. В результаті виникає наступна математична задача. Нехай функція 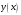 задана таблицею: задана таблицею: 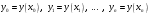 . .Потрібно побудувати інтерполянту – функцію 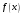 , котра співпадає з функцією , котра співпадає з функцією 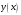 в точках в точках 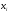 : :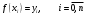 (1. 1. 1) (1. 1. 1)Основна мета інтерполяції – отримати швидкий алгоритм обчислення значень 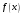 і оцінити похибку і оцінити похибку 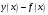 . Інтерполюючі функції . Інтерполюючі функції 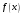 , як правило, будуються в вигляді лінійних комбінацій деяких елементарних функцій: , як правило, будуються в вигляді лінійних комбінацій деяких елементарних функцій: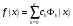 , де , де 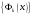 - фіксовані лінійно незалежні функції, - фіксовані лінійно незалежні функції, 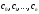 - не визначені поки що коефіцієнти. - не визначені поки що коефіцієнти.Із умов (1. 1. 1) отримуємо систему п+1 рівнянь відносно коефіцієнтів 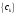 : : 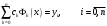 . .Припустимо, що система функцій 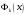 така, що при будь-якому така, що при будь-якому 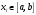 відмінний від нуля визначник системи: відмінний від нуля визначник системи: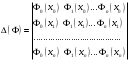 . .Тоді по заданим 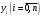 однозначно визначаються коефіцієнти однозначно визначаються коефіцієнти 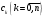 . В якості системи лінійно незалежних функцій . В якості системи лінійно незалежних функцій 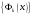 частіше обирають: степеневі функції частіше обирають: степеневі функції 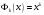 (в цьому випадку (в цьому випадку 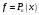 - поліном степені п); тригонометричні функції - поліном степені п); тригонометричні функції 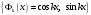 (f - тригонометричний поліном); використовують також раціональні функції та ін. (f - тригонометричний поліном); використовують також раціональні функції та ін. В даній курсовій роботі розглядаються інтерполяційні поліноми. Відомо, що будь-яка неперервна на відрізку 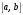 функція функція 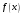 може бути добре наближена деяким поліномом може бути добре наближена деяким поліномом 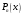 (див. [1], c.50): (див. [1], c.50):Теорема Вейерштрасса: Для будь-якого 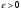 існує поліном існує поліном 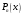 степеня степеня 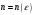 , такий, що , такий, що 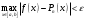 . .Отже, будемо шукати інтерполяційний поліном в вигляді: 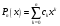 , (1. 1. 2) , (1. 1. 2)де 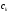 - невизначені коефіцієнти. Покладемо - невизначені коефіцієнти. Покладемо 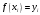 , тоді отримаємо систему лінійних рівнянь: , тоді отримаємо систему лінійних рівнянь: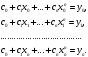 Визначник даної системи являється відмінним від нуля визначником Вандермонда (див. [9]): 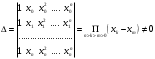 . .Звідси випливає, що інтерполяційний поліном (1. 1. 2) існує і він єдиний, хоча форм його запису існує багато. В якості базису 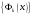 ми взяли базис із одночленів ми взяли базис із одночленів 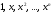 . Для обчислень більш зручним являється базис поліномів Лагранжа . Для обчислень більш зручним являється базис поліномів Лагранжа 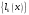 степеня п або коефіцієнтів Лагранжа: степеня п або коефіцієнтів Лагранжа: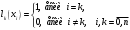 Неважко побачити, що поліном степені п 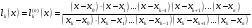 задовольняє цим умовам. Полином 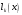 , очевидно, визначається єдиним способом. Дійсно, нехай існує ще один поліном , очевидно, визначається єдиним способом. Дійсно, нехай існує ще один поліном 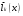 , тоді їх різниця , тоді їх різниця 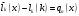 є поліном степені п, який перетворюється в нуль в п+1 точках є поліном степені п, який перетворюється в нуль в п+1 точках 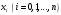 . Це можливо тільки при . Це можливо тільки при 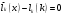 . .Поліном 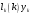 приймає значення приймає значення 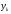 в точці в точці 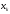 і рівний нулю у всіх останніх вузлах і рівний нулю у всіх останніх вузлах 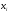 при при 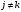 . Звідси випливає, що інтерполяційний поліном: . Звідси випливає, що інтерполяційний поліном: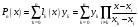 (1. 1. 3) (1. 1. 3)має степінь не вище п і 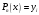 . Формулу (1. 1. 3) називають формулою Лагранжа. Число арифметичних дій для обчислення по (1. 1. 3) пропорційно . Формулу (1. 1. 3) називають формулою Лагранжа. Число арифметичних дій для обчислення по (1. 1. 3) пропорційно 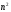 . Для оцінки близькості полінома . Для оцінки близькості полінома 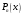 до функції до функції 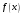 покладають, що існує п+1– ша неперервна похідна покладають, що існує п+1– ша неперервна похідна 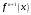 . Тоді має місце формула для похибки . Тоді має місце формула для похибки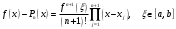 . .При оцінці похибки результатів повинні враховуватись як похибки методу інтерполяції (залишковий член), так і похибка округлення при обчисленнях. 1.2 Інтерполяційні формули Ньютона Часто інтерполювання ведеться для функцій, заданих таблицями з рівновіддаленими значеннями аргументу (тобто такими, що будь-який 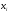 (вузол інтерполяції) можна представити у вигляді (вузол інтерполяції) можна представити у вигляді 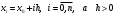 - деяка постійна величина, яка називається кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а також проведення обчислень по ним значно спрощується. - деяка постійна величина, яка називається кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а також проведення обчислень по ним значно спрощується.Для побудови формули Ньютона необхідно ввести поняття кінцевих різниць. Кінцевими різницями називають різниці між значеннями функції в сусідніх вузлах (точках 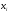 ) інтерполяції: ) інтерполяції: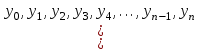  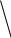  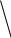  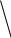  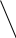 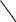 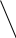   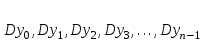 де 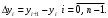 Отримані кінцеві різниці будемо називати кінцевими різницями першого порядку. З різниць першого порядку отримаємо різниці другого порядку: Отримані кінцеві різниці будемо називати кінцевими різницями першого порядку. З різниць першого порядку отримаємо різниці другого порядку: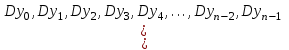        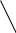 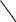 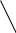   де 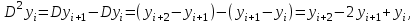 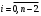 . .Повторюючи процедуру, отримаємо кінцеві різниці третього порядку: 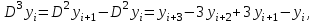 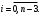 Для кінцевих різниць 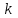 -го порядку: -го порядку: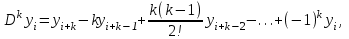 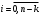 В результаті отримаємо таблицю кінцевих різниць: 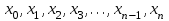 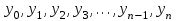   |
