Реферат Формилизованные методы системного анализа. Формализованные методы системного анализа. Введение формализованные методы системного анализа (методы формализованного представления систем, мфпс)

• Название: Введение формализованные методы системного анализа (методы формализованного представления систем, мфпс)
• Анкор: Реферат Формилизованные методы системного анализа
• Дата: 11.04.2023
• Размер: 131.62 Kb.
• Имя файла: Формализованные методы системного анализа.docx
• Тип: Реферат; #1054929

СОДЕРЖАНИЕ

Введение 3

1. Классификация методов формализованного представления систем 4

2. Прикладные классификации МФПС 19

3. Заключение 23

4. Список литературы 24

ВВЕДЕНИЕ
Формализованные методы системного анализа (методы формализованного представления систем, МФПС) – класс методов, выделенный в классификации моделирования систем, предложенный в [5].

Математика непрерывно развивается. Возникают новые области и математические теории, отмирают или вливаются в другие математические разделы. Исследованием структуры (или, как принято говорить, архитектуры) математики занимаются многие ученые (см., например, [2, 7, 8, 10, 11, 12, 14 и др.]).

Несмотря на том, что в практике моделирования широко используются теория множеств, математическая логика, математическая лингвистика и другие направления современной математики, до сих пор еще не все ученые-математики склонны включать в число математических некоторые из этих направлений. Благодаря работам французских ученых (опубликовавшим свои работы по псевдонимом Н. Бурбаки [3]), теорию множеств и математическую логику стали признавать разделами математики, а математическую лингвистику и семиотику часто еще не относят к математике. Поэтому, чтобы не обсуждать различные точки зрения (которые постепенно изменяются, развиваются), вместо термина «математические методы» удобнее применять предложенный в [5] термин «методы формализованного представления систем».

1. 
   Классификация методов формализованного представления систем
   

В большинстве первоначально применявшихся при исследовании систем классификаций выделяли детерминированные и вероятностные (статистические) методы или классы моделей, которые сформировались в конце прошлого столетия. Затем появились классификации, в которых в самостоятельные классы выделились теоретико-множественные представления, графы, математическая логика и некоторые новые разделы математики.

Например, в классификации современного математического аппарата инженера В.П. Сигорским [11] выделяются: множества, матрицы, графы, логика, вероятности.

В одной из первых классификаций, предложенных специально для целей системных исследований украинским академиком А.И. Кухтенко [9], наряду с выделением таких уровней математического абстрагирования, как общеалгебраический, теоретико-множественный, логико-лингвистический, предлагается рассматривать информационный­ и эвристический уровни изучения сложных систем.

Имеются и другие классификации (см., например, [13]).

Ниже кратко характеризуется классификация Ф.Е. Темникова, предложенная в [5], в которой выделяются следующие обобщенные группы (классы) методов (табл. 1):

• 
  аналитические, к которым в рассматриваемой классификации отнесены методы классической математики, включая интегро-дифференциальное исчисление, методы поиска экстремумов функций, вариационное исчисление и т.п.; методы математического программирования; первые работы по теории игр и т.п.;
  
• 
  статистические, включающие и теоретические разделы математики – теорию вероятностей, математическую статистику, и направления прикладной математики, использующие стохастические представления – теорию массового обслуживания, методы статистических испытаний (основанные на методе Монте-Карло). методы выдвижения и проверки статистических гипотез А. Вальда и другие методы статистического имитационного моделирования;
  
• 
  теоретико-множественные, логические, лингвистические, семиотические, представления (методы дискретной математики), составляющие теоретическую основу разработки языков моделирования, автоматизации проектирования, информационно-поисковых языков;
  
• 
  графические, включающие теорию графов и разного рода графические представления информации типа диаграмм, гистограмм и других графиков.
  

Разумеется, в табл. 1. приведены лишь укрупненные группы-направления, конкретные методы которых только в начальный период развития характеризуются рассмотренными особенностями. Эти направления непрерывно развиваются, и в их рамках появляются методы с расширенными возможностями по сравнению с исходными.

Кроме того, в математике постоянно возникают новые направления как бы «на пересечении» методов, отнесенных в приведенным укрупненным группам.

В частности, на пересечении аналитических и теоретико-множественных представлений возникла и развивается алгебра групп; параллельно в рамках алгебры групп и теории множеств начала развиваться комбинаторика; теоретико-множественные и графические представления стали основой возникновения топологии; статистические и теоретико-множественные методы инициировали возникновение теории размытых множеств Л. Заде, которая, в свою очередь, явилась началом развития нового направления – нечетких формализаций и т.д.

Практически невозможно создать единую классификацию, которая включала бы все разделы современной математики. В то же время приведенные направления помогают понять особенности конкретных методов. использующие средства того или иного направления или их сочетания, помогают выбирать методы для конкретных приложений.

Название класса методов и символический образ	Основная терминология и примеры теорий, возникших и развивающихся на базе соответствующего класса методов	Сферы и возможности применения
Аналитические методы	Аналитическими здесь названы методы, которые ряд свойств многомерной, многосвязной системы отображают в n-мерном пространстве в виде одной единственной точки (безразмерной в строгих математических доказательствах), совершающей какое-либо перемещение в пространстве (или обладающую каким-то поведением). Это отображение осуществляется посредством оператора (функции, функционала) Ф[Sx]. Можно также две (или более) системы или их части отобразить точками и рассматривать взаимодействие этих точек. Поведение точек, их взаимодействие описываются строгими соотношениями, имеющими силу закона. Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики (величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т.д.). На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа (методов исследования функций, их вида, способов представления, поиска экстремумов функций и т.п.) до таких новых разделов современной математики, как математическое программирование (линейное, нелинейное, динамическое и т.п.), теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т.п.)	Применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или зависимостей, т.е. когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала. Эти методы используются при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, оптимальной стратегии поведения, в том числе в конфликтных ситуациях и т.п. Математические теории, развивающиеся на базе аналитических представлений, направления стали основой многих прикладных теорий, в том числе теории автоматического управления, теории оптимальных решений и т.д. При практической применении аналитических представлений для отображения сложных систем следует иметь ввиду, что они требуют установления всех детерминированных связей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем получить требуемые аналитические зависимости крайне трудно. Более того, даже если это и удается. то практически невозможно доказать правомерность применения таких выражений, т.е. адекватность модели рассматриваемой задачи.
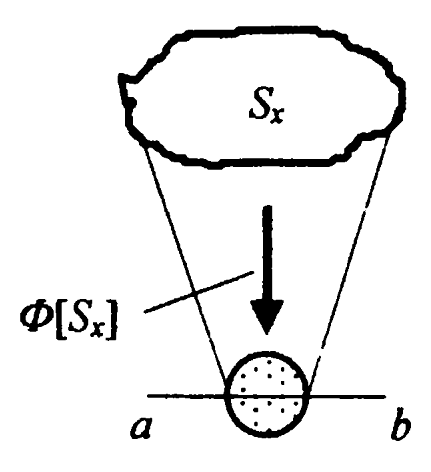
Статистические методы	Статистическим называют отображение системы с помощью случайных (стохастических) событий, процессов, которые описываются вероятностными характеристиками и статистическими закономерностями. Статистические отображения можно представить (см. символический образ) как бы в виде «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (ее учитываемые в модели свойства) оператор Ф[Sx]. «Размытую» точку следует понимать как некоторую область, характеризующую движение системы ее (поведение); при этом границы области заданы с некоторой вероятность p (под вероятностью событий понимается p(A) = m/n, где m – число появлений события A, n – общее число опытов; если n → ∞ (m/n) → const), т.е. ка как бы размыты, и движение точки описывается некоторой случайной функцией. Закрепляя все параметры этой области, кроме одного, можно получить срез по линии a – b, смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трехмерную и т.д. картины статистического распределения. На базе статистических представлений развивается ряд математический теорий: математическая статистика; теория статистических испытаний (основой которой является метод Монте-Карло), а развитием – теория статистического имитационного моделирования; теория выдвижения и проверки статистических гипотез, базирующаяся на общей теории статистически решающих функций А. Вальда (частным случаем этой теории, важным для теории систем, является байесовский подход к исследованию передачи информации в процессах общения, обучения и др. ситуациях); теория потенциальной помехоустойчивости и теории решающих функций; обобщение последних двух направлений – теория статистических решений.	На базе статистических представлений возникли и развиваются прикладные направления: статистическая радиотехника, статистическая теория распознавания образов, экономическая статистика, теория массового обслуживания; а также развившиеся из направлений, возникших на базе аналитических представлений, - стохастическое программирование, новые разделы теории игр и т.п. Расширение возможностей отображения сложных систем и процессов по сравнению с аналитическими методами можно объяснить тем, что при применении статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все детерминированные связи между изучаемыми объектами (событиями) или учитываемыми компонентами сложной системы, на основе выборочного исследования (исследования репрезентативной выборки) получать статистические закономерности и распространять их на поведение системы в целом с какой-то вероятностью. Однако не всегда можно получить статистические закономерности, не всегда может быть определена репрезентативная выборка, доказана правомерность применения статистических закономерностей. Если же не удается доказать репрезентативность выборки или для этого требуется недопустимо большое время, то применение статистических методов может привести к неверным результатам. В таких случаях целесообразно обратиться к методам, объединяемым под общим названием – методы дискретной математики, которые помогают разрабатывать языки моделирования, модели и методики постепенной формализации процесса принятия решения. Статистические и теоретико-множественные методы инициировали возникновение теории нечетких или размытых множеств Л. Заде, которая явилась началом развития нового направления – нечетких формализаций и т.д.
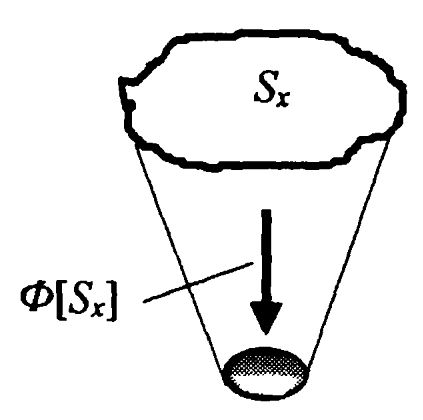
Теоретико-множественные представления	Теоретико-множественные представления базируются на понятиях множество, элементы множества, отношения на множествах, континуум. Множества могут задаваться следующими способами: перечислением (интенсионально): {ai}, где i = 1..n или <a1,a2, … , ai, … , an>, где ai A; путем указания некоторого характеристического свойства A(экстенсионально). В основе теоретико-множественных преобразований лежит переход от одного способа задания множества к другому. В множестве могут быть выделены подмножества. Из двух или нескольких множеств можно сформировать путем установления отношений между элементами этих множеств новое множество, обладающее принципиально новыми свойствами и, как правило, новое качество приобретают и элементы. Теоретико-множественными описаниями разных систем или частей можно устанавливать соответствия: гомоморфизма, изоморфизма, автоморфизма, отношения рефлексивности, симметричности, транзитивности, заимствованные теорией множеств из других разделов математки.	Благодаря возможности введения любых отношений теоретико-множественные представления используются как обобщающий язык при сопоставлении различных направлений математики и других дисциплин, явились основой для возникновения новых научных направлений или развития существующих. В частности, теоретико-множественные представления получили широкое распространение для уточнения ряда математических направлений (первой теорией, для которой на основе этих представлений были получены важные новые результаты, была теория числен); сыграли большую роль в становлении комбинаторики, топологии, в разработке теории «размытых» множеств Л. Заде: на их основе стали создаваться первые информационно-поисковые языки, языки автоматизации моделирования; на теоретико-множественных представлениях базируется вариант математической теории систем М. Месаровича. Система может быть представлена совокупностью мноеств и подмножеств разнородных компонентов с произвольно вводимыми элементами и отношениями. Однако свобода введения произвольных отношений приводит к тому, что в формализованном с их помощью описании проблемной ситуации довольно быстро могут обнаружиться неразрешимые противоречия – парадоксы, апории или антиномии, что не позволяет оперировать с получаемыми теоретико-множественными моделями таким же образом, как с классическими математическими (аналитическими, статистическими) соотношениями, гарантируя достоверность получаемых результатов.
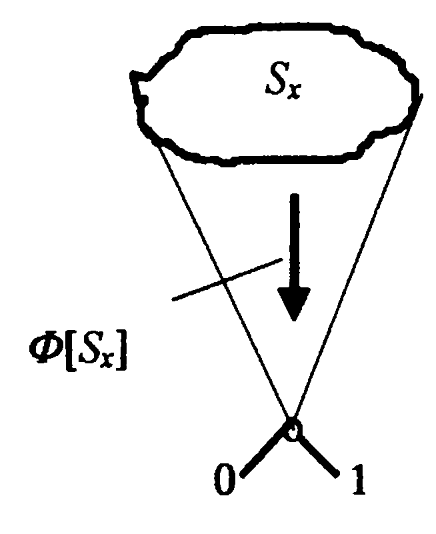
Логические методы или математическая логика	Логические представления переводят реальную систему и отношения в ней на язык одной из алгебр логики (двузначной, многозначной), основанной на применении алгебраических методов для выражений законов алгебры логики. Наибольшее распространение получила бинарная алгебра логики Буля (булева алгебра). Базовыми понятиями алгебры логики являются высказывание, предикат, логические функции (операции), кванторы, логический базис, логические законы или теоремы (законы алгебры логики), применяя которые можно преобразовать систему из одного описания в другие с целью ее совершенствования. Например, получить более простую структура (схему), содержащую меньшее число состояний, элементов, но осуществляющую требуемые функции. Теоремы доказываются и используются в рамках формального логического базиса, определяемого совокупностью специальных правил. Логические методы представления систем относятся к детерминистским, хотя возможно их расширение в сторону вероятностных оценок. На базе математической логики созданы и развиваются теории логического анализа и логического синтеза, теории автоматов. На основе логических представлений первоначально начинали развиваться некоторые разделы теории формальных языков. В силу ограниченности смысловыражающих возможностей бинарной алгебры логики в послежнее время имеются попытки создания многозначных (тернарной и т.п.) алгебр логики с соответствующими логическим базисами и теоремами.	Применяются при исследовании новых структур и систем разнообразно природы (технических объектов, текстов и др.), в которых характер взаимоотношений между элементами еще не настолько ясен, чтобы было возможно их представление аналитическими методами, а статистические исследования либо затруднены, либо не привели в выявлению устойчивых статистических закономерностей. В то же время следует иметь в виду, что с помощью логических алгоритмов можно описывать не любые отношения, а только те, которые предусмотрены законами алгебры логики и удовлетворяют требованиям логического базиса. Логические представления широко применяются при исследовании и разработке автоматов разного рода, автоматическим систем контроля, при решении задач распознавания образов. На их основе развивается самостоятельный раздел теории формальных языков – языки моделирования проблемных ситуаций и текстов. В то же время смысловыражающие возможности логических методов ограничены базисом и не всегда позволяют адекватно отобразить реальную проблемную ситуацию. Поэтому стали предприниматься попытки создания вначале тернарной логики, а затем и многозначных логик, вплоть до непрерывной. Однако попытки создания многозначных логик на практике пока не находят широкого применения из-за сложности обоснования логического базиса и доказательства формальных теорем-законов многозначной алгебры логики, без чего невозможно формально применять логические законы и алгоритмы и получать достоверные результаты.
Лингвистические и семиотические представления или математическая лингвистика и семиотика	Основными понятиями, на которых базируются лингвистические представления, являются понятия: тезаурус T, грамматика G, семантика, прагматка. Термин тезаурус (от греч. θηδαυρος, thesaurus – сокровищница, богатство, клад, запас и т.п.) в общем случае характериузет «совокупность научных знаний о явлениях и законах внешнего мира и духовной деятельности людей, накопленную всем человеческим обществом». В математической лингвистике и семиотике термин тезаурус используется в более узком смысле для характеристики конкретного языка, его многоуровневой структуры. Для этих целей удобно пользоваться одним из принятых в лингвистике определений тезауруса как «множества смысловыражающих элементов языка с заданными смысловыми отношениями», которое дал Ю.А. Шрейдер. Для системных приложений интересно сочетание математической лингвистики и семиотики, которая возникла как наука о знаках, знаковых системах. Однако некоторые школы, развивающие семиотические представления, равноправно пользуются в семиотике понятиями математической лингвистики, такими как тезаурус, грамматика, семантика и т.п. Такие представления иногда называют лингвистической семиотикой или лингвосемиотикой. С теоретической точки зрения границу между лингвистическими и семиотическими представлениями при разработке языков моделирования можно определить характером правил грамматики: если правила не охватываются классификацией нормальных грамматик Н. Хомского, то модель относят к семиотической и применяют произвольные правила взаимоотношений между знаками, отображающими компоненты модели, допустимые семиотикой.	Для практических приложений модели лингвистических и семиотических представлений можно рассматривать как один класс методов формализованного представления систем. Лингвистические и семиотические представления возникли и развиваются в связи с потребностями анализа текстов и языков. Однако во второй половине XX в. эти представления стали широко применяться для отображения и анализа процессов в сложных системах в тех случаях, когда не удается применить сразу аналитические, статистические представления или методы формальной логики. В частности, лингвистические и семиотические представления являются удобным аппаратом (особенно в сочетании с графическими) для первого этапа постановки и формализации задач принятия решений в ситуациях с большой начальной неопределенностью, чем и был вызван интерес к этим методам со стороны инженеров и специалистов, занимающихся исследованием и разработкой сложных систем. На их основе разрабатывают языки моделирования и автоматизации проектирования. При применении этих методов следует иметь в виду, что при усложнении языка моделирования, при применении правил произвольной грамматики или семиотики трудно гарантировать достоверность получаемых результатов, возникают проблемы алгоритмической разрешимости парадоксов, которые частично могут быть преодолены с помощью содержательного контроля и корректировки языка на каждом шаге его расширения в диалоговом режиме моделирования. При этом разработчик языка моделирования не всегда может формально объяснить его возможности, происходит как бы «выращивание» языка, у которого появляются новые свойства, повышающие его смысловыражающие возможности.
Графические представления	К графическим представлениям здесь отнесены любые графики (диаграммы, гистограммы, графики Ганта, т.е. «время-операция» в прямоугольных координатах и т.п.) и возникшие на основе графических отображений теории: теорию графов, теорию сетевого планирования и управления и т.п., т.е. все, что позволяет наглядно представить процессы, происходящие в системах, и облегчить таким образом их анализ для человека (лица, принимающего решения). Графики Гента выполнялись с ручным, а в последующем и с автоматическим управлением. В последующем на этой основе возникли представления совокупности дискретных операций в дискретном времени как множества событий, упорядоченных в двух измерениях – сетевые структуры. Есть и возникшие на основе графических представлений методы, которые позволяют ставить и решать вопросы оптимизации процессов организации, управления, проектирования и являются математическими методами в традиционном смысле. Таковы геометрия, теория графов. Понятие графа в математическом смысле первоначально было введено Л. Эйлером.	Графические представления являются удобным средством исследования структур и процессов в сложных системах, средством организации взаимодействия человека и технических устройств (в том числе ЭВМ). На основе сетевых структур возникли прикладные теории: PERT (Program Evaluation and Review Technique – Методика оценки и контроля программ), теория сетевого планирования и управления (СПУ). Первоначально СПУ широко применялись не только в управлении производственными процессами (где достаточно несложно построить сетевой график), но и в системах организованного управления. Однако применение СПУ ограничивается ее недостатками: теория первоначально была ориентирована на анализ только одного класса графов – направленных (не имеющих обратных связей, т.е. циклов, петель); доля «ручного» труда ЛПР при разработке сетевого графика составляет по оценкам специалистов до 95% общих затрат времени и на анализ ситуаций и процессов с использованием СПУ. Поэтому разрабатываются методы статистического сетевого моделирования с использованием вероятностны оценок и ненаправленных графов, подходы в автоматизации формирования графов.

2. 
   Прикладные классификации МФПС
   

Для удобства выбора методов решения реальных практических задач на базе математических направлений развиваются прикладные и предлагаются их классификации.

Так, существуют различные классификации экономико-математических методов, обобщение которых приведено в табл. 2. Эта классификация включает прикладные направления, базирующиеся, в основном, на использовании аналитических и статистических представлений. Однако некоторые из них (модели объемного и календарного планирования, потоковые модели) используют графические методы (сетевое моделирование), а иногда для предварительного описания задачи – теоретико-множественные представления.

Когда начали широко развиваться автоматизированные системы сбора, хранение и поиска информации разного рода, появилась потребность в разработке классификаций методов работы с информационными массивами. Одна из таких классификаций, предложенная в [1], приведена в нижней части табл. 2. Эти классификации, напротив, базируются на использовании методов дискретной математики, в основном графических и теоретико-множественных представлений с элементами математической логики. Классификации, ориентированные на прикладные направления, можно сопоставить с классификациями математических методов, что сделано в табл. 2. Получаемая двумерная классификация удобна тем, что в нее можно «входить» через прикладные направления («слева») и через математические («сверху»), что помогает при организации взаимодействия проектировщиков и управленческих работников, использующих прикладные классификации, со специалистами-математиками, которые помогут пояснить принципиальные теоретические возможности выбираемых математических методов.

Таблица 2

Прикладные классификации методов моделирования	Классификация методов формализованного представления систем
	Аналитические	Статистические	Теоретико-множественные	Логические	Лингвистические	Графические
Экономико-математические методы
Производственные функции	+	+
Балансные модели	+		+
Модели объемного планирования	+		+			+
Модели календарного планирования (упорядочения во времени, расписания)	+
Потоковые (транспортные) модели	+					+
Модели распределения и назначения	+
Модели управления запасами	+	+
Модели износа и замены оборудования	+	+
Модели массового обслуживания		+
Состязательные модели	+	+
Методы работы с массивами информации
Методы организации массивов			+	+		+
Методы обработки массивов (сортировки, упорядочения, размещения)			+	+
Методы поиска информации			+	+	+

При выборе метода моделирования для постановки принципиально новых задач с большой начальной неопределенностью удобно связать классификацию методов формализованного представления с классификацией систем. В частности, приведенную в таблице классификацию методов формализованного представления систем можно связать с классификацией систем по степени организованности: если предварительный анализ проблемной ситуации показывает, что она может быть представлена в видео хорошо организованных систем, то можно выбирать метода моделирования из классов аналитических и графических методов; если специалисты по теории систем и системному анализу рекомендуют представить ситуацию в виде плохо организованных или диффузных систем, то следует обратиться прежде всего к статистическому моделированию, а если не удастся доказать адекватность ее применения, то – искать закономерности в специальных методах (например, в экономике, социологии и т.п.); при представлении ситуации классом самоорганизующихся систем следует применять методы дискретной математики, разрабатывая их на основе языка моделирования и автоматизации проектирования, и, как правило, - формировать модель, сочетая методы из групп МАИС и МФПС.

Следует оговорить, что любая классификация методов всегда может быть подвергнута критике. Однако, понимая условность классификации, ее все же нужно создавать. Желательно, чтобы такую классификацию формировал коллектив, разрабатывающий и применяющий модель или методику системного анализа. Это позволит ему в более сжатые сроки выбрать методы моделирования для выполнения того или иного этапа методики системного анализа.

Все методы современной математики не может глубоко знать ни один специалист, однако при выборе метода важно понимать особенности того или иного направления и возможности его использования, а, выбрав метод, пригласить соответствующих специалистов, владеющих им. Выбор метода зависит от предшествующего опыта разработчиков и управленческих работников. Ошибки в выборе методов моделирования на начальных этапах постановки задачи могут существенно повлиять на дальнейших ход работ, затянуть их или привести в тупик, когда решение вообще не будет получено.
ЗАКЛЮЧЕНИЕ
В настоящей работе были рассмотрены теоретические и прикладные классификации основных формализованных методов системного анализа (методы формализованного представления систем, МФПС).

1. 
   в настоящее время существует достаточное количество формализованных методов, позволяющих решат большое количество прикладных задач;
   
2. 
   однако, их разработка далеко не завершена; так для некоторых прикладных задач все еще не существует адекватных формализованных методов и для них необходимо использовать специальные методики (например, в экономике, социологии и т.д.);
   
3. 
   кроме того, не завершена и теоретическая разработка МФПС; так, не все разделы математики, наработки которых используют формализованные методы, считаются таковыми всем ученым математическим обществом;
   
4. 
   рассмотренные в работе классификации МФПС имеют не только теоретическое, но и важное прикладное значение, т.к. упрощают выбор нужной методики моделирования для той или иной задачи.
   

СПИСОК ЛИТЕРАТУРЫ

1. 
   Автоматизированные системы управления предприятиями: Учебное пособие / Под ред. В.Н. Четвериова. – М.: Высш. школа, 1979. – 308 с.
   
2. 
   Архитектура математики / Под ред. Б.В. Гнеденко. – М.: Знание, 1972. – 24 с.
   
3. 
   Бурбаки Н. Теория множеств. – М.: Мир, 1965. – 398 с.
   
4. 
   Волкова В.Н., Денисов А.А. Основы теории систем и системного анализа: Учебник для студентов вузов. – СПб.: Изд-во СПбГТУ, 1997. – С. 130-145
   
5. 
   Волкова В.Н., Темников Ф.Е. Методы формализованного представления (отображения) систем: Текст лекций. – М.: ИПКИР, 1974. – 114 с.
   
6. 
   Волкова В.Н., Денисов А.А., Темников Ф.Е. Методы формализованного представления систем: Учебное пособие. СПб.: СПбГТУ, 1993. – 107 с.
   
7. 
   Гнеденко Б.В. Математика в современном мире. – М.: Просвещение, 1980. – 128 с.
   
8. 
   Кудрявцев Л.Д. Современная математика и ее преподавание. – М.: Наука, 1985. – 170 с.
   
9. 
   Кухтенко А.И. Об аксиоматическом построении математической теории систем // Кибернетика и вычислительная техника. – Киев: Наукова думка, 1976. С. 3-25.
   
10. 
    Рыбников К.А. История математики: Учебник. – М.: Изд-во МГУ, 194. – 496 с.
    
11. 
    Сигорский В.П. Математический аппарат инженера. – Киев: Техника, 1977. – 766 с. 12.
    
12. 
    Стройк Д.Я. Краткий очерк истории математики. – М.: Наука, 1990. – 253 с. 13.
    
13. 
    Технология системного моделирования / Е.Ф. Аврамчук, А.А. Вавилов, С.В. Емельянов и др. – М.: Машинстроение; Берлин: Ферлаг Текник, 1988. – 519 с.
    
14. 
    Фор. Р., Коффман А., Дени-Папен М. Современная математика. – М.: Мир, 1966
    
15. 
    Ершов В.В. Правовое и индивидуальное регулирование общественных отношений: Монография. – М.: РГУП, 2018. – 628 с.
    
16. 
    Ершов В.В. Регулирование правоотношений: Монография. – М.: РГУП, 2020. – 564 с.
    
17. 
    Ловцов Д.А. Информационная теория эргасистем. Тезаурус: Монография. – М.: Наука, 2005. – 248 с.
    
18. 
    Ловцов Д.В. Системология правового регулирования: исторические аспекты развития // История государства и права. – 2009. - № 18. – С. 9 – 12.