Лекции_Введение_в_нанотехнологии. Введение в нанотехнологии

• Название: Введение в нанотехнологии
• Дата: 16.10.2022
• Размер: 5.09 Mb.
• Имя файла: Лекции_Введение_в_нанотехнологии.doc
• Тип: Документы; #737269
• страница: 2 из 24

Глава 1. Квантовые эффекты в нанотехнологиях

Уникальные свойства наноматериалов определяются тем фактом, что с размера менее 100 нм становятся существенными квантовые эффекты, которые подчиняются законам квантовой механики. Днем рождения квантовой механики считается 14 декабря 1900 года, когда Макс Планк на заседании Немецкого физического общества сделал предположение, что энергия света излучается квантами (квант от лат. quant – сколько). При этом энергия одного кванта должна быть пропорциональна частоте:

(1.1)

где Дж/с – постоянная Планка; и .

Соответственно энергия светового потока будет равна:

(1.2)

где n = 1, 2, 3… – целые числа или количество квантов.

Слово «квант» дало название квантовой механике. Под квантованием энергии понимается тот факт, что энергия может принимать только дискретные значения из какого-либо разрешенного набора значений. Данный факт становится актуальным при рассмотрении атомов и молекул, а также квантовых точек. Энергия квантовых точек, как и у атомов, принимает дискретные значения, поэтому квантовые точки иногда называют искусственными атомами.

В 1927 году произошла квантовая революция в физике – были экспериментально обнаружены волновые свойства электрона. Независимо друг от друга два исследователя К.Д. Дэвиссон и Джордж Томсоном обнаружили явление дифракции электронов на монокристаллах никеля. Гипотезу о волновой природе частиц выдвинул в 1924 году французский ученый Луи де Бройль, и уже через три года она подтвердилась. Согласно его предположению свободное движение частицы с массой m и скоростью υ можно представить как монохроматическую волну, называемую также волной де Бройля, с длиной волны и распространяющуюся в том же направлении, в котором движется частица (рис. 1.1).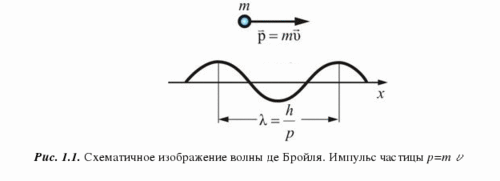



Рис. 1.1. Схематичное изображение волны де Бройля. Импульс частицы p=mv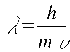

(1.3)

Длина волны мячика массой 0,20 кг, движущегося со скоростью 15 м/с, равна 2,2 · 10-34 м. В мире не существует инструментов, позволяющих определить такую малую величину, поэтому нам не видны волновые свойства мячика. Напротив, длина волны электрона, ускоренного разностью потенциалов в 100 В, равна 1,2 · 10-10 м, или 0,12 нм, что как раз соответствует межатомному расстоянию в кристалле никеля.

Из формулы (1.3), видно, что, меняя энергию электрона, можно менять его длину волны. Этот факт с успехом используется в современных электронных микроскопах, когда, управляя энергией электронов, меняют его длину волны и, соответственно, разрешающую способность микроскопа. После открытия волновых свойств электрона квантовая механика, а затем и ядерная физика получили бурное развитие. Кроме атомной бомбы и атомной энергетики успехам квантовой физики также обязана и теория твердого тела, которая изучает закономерности строения вещества на макро-, микро- и наноуровнях. Основные эффекты, применяемые в нанотехнологиях, связаны с зонной теорией, или теорией энергетических зон.

Нанотехнология, в отличие от ядерной физики, имеет дело не с атомами, а с молекулами, кластерами и нанокристаллами. Молекула, как правило, состоит из нескольких атомов, кластер – из нескольких десятков и сотен атомов, нанокристалл – из нескольких сотен и тысяч атомов, а монокристалл – из более чем 1018 атомов. Интересно, что при переходе от единичного атома к молекуле, кластеру или нанокристаллу в расположении энергетических уровней происходят существенные изменения.

Первые три значения из энергетического набора значений одиночного атома, называемого также спектром значений, представлены на рис. 1.2 а.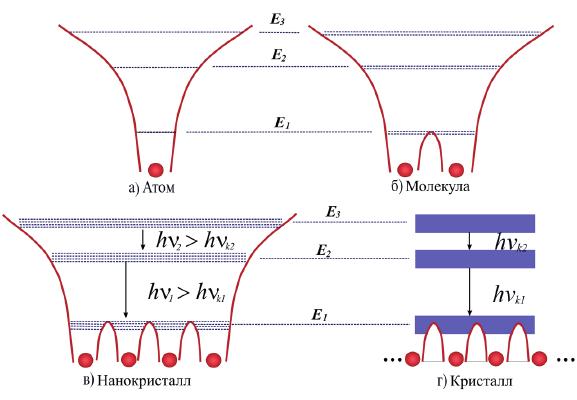



Рис. 1.2. Расположение уровней в атоме (а), молекуле (б), нанокристалле (в), кристалле (г)

Согласно принципу Паули на одном энергетическом уровне запрещается нахождение более двух электронов. В результате при приближении одного атома к другому уровни расщепляются на два (рис. 1.2 а, б). При добавлении десятков, сотен и тысяч атомов уровни расщепляются на такое же количество подуровней (рис. 1,2 в). Таким образом, образуется нанокристалл, расстояние между уровнями уменьшаются, но они остаются дискретными и различимыми. В том случае, когда образуется монокристалл (рис. 1.2 г), количество атомов становится равным 1018 и более, а расстояние между уровнями – порядка 10-18 эВ, следовательно, уровни становятся неразличимыми.

Непрерывную группу энергетических уровней принято называть зоной.

Выделяют разрешенную и запрещенную зоны. Разрешенная зона – зона, где находятся уровни энергии, электрону там находится разрешено. Запрещенная зона – зона, где уровней нет, и электрону там находится запрещено.

При переходе от кристалла к нанокристаллу видно, что переходы между уровнями увеличиваются (рис. 1.2 г, в). Данный эффект получил название квантоворазмерного эффекта – при уменьшении размера наночастиц энергия между энергетическими переходами, а значит и энергия квантов излучения увеличивается. Именно поэтому цвета окраски и излучения коллоидных растворов наночастиц зависят от их размера. Квантоворазмерный эффект играет огромную роль в нанотехнологиях. Например, варьируя технологическими параметрами размер нанокристаллов, можно получать различные цвета электролюминесценции.

Энергетическая зона, образованная валентными электронами носит название валентной зоны.

Зона, лежащая выше валентной, называется зоной проводимости.

Кристаллы являются диэлектриками или проводниками (металлами) в зависимости от того, как заполнены их валентная зона и зона проводимости.

В диэлектриках валентная зона заполнена электронами, а зона проводимости – пуста. Металлы отличаются от диэлектриков тем, что в них зона проводимости заполнена частично, а валентная зона – полностью.

Полупро­водники – это частный случай диэлектриков: при низкой температуре (менее 150-200 К) у них валентная зона тоже заполнена, а зона проводимости практически пуста. Особенностью полупроводников, по сравнению с другими диэлектриками, является сравнительно узкая запрещен­ная зона. За счет энергии теплового движения часть электронов уже при комнатной температуре может ее преодолеть и оказаться в зоне проводимости. Ситуация похожа на испарение жидкости, когда самые быстрые молекулы могут покинуть ее поверхность и перейти в воздух. Электроны в зоне проводимости могут направленно двигаться в электрическом поле и создавать ток, а электроны в валентной зоне – не могут. Поэтому при низких температурах полупроводники ток не проводят, а при высоких – проводят. Отсюда и название – полупроводник.

Комбинируя два типа полупроводников с запрещенными зонами E_g1 и E_g2 можно получить либо потенциальный барьер, либо квантовую яму (рис. 1.3).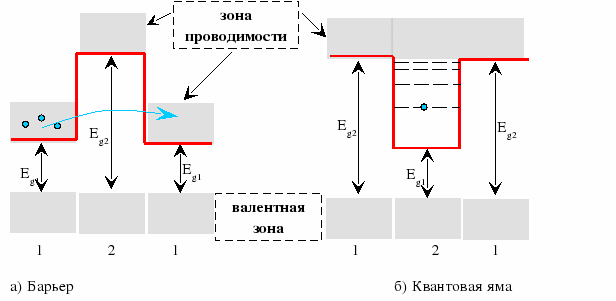



Рис. 1.3. Формирование квантовых барьеров (а) и квантовых ям (б)

Вначале в качестве простого примера рассмотрим потенциальный барьер в классическом случае – шарик катится в поле силы тяжести.

Кривая на рис. 1.4 а изображает его траекторию, «горка» называется потенциальным барьером, потому что с высотой h подъема шарика его потенциальная энергия должна возрастать, а кинетическая энергия из-за этого – падать.

Высотой потенциального барьера называется потенциальная энергии частицы на «вершине горки» U = mgh (m – масса частицы, g – ускорение свободного падения).

Если кинетическая энергия частицы E_кин больше высоты потенциального барьера U – частица перекатится на другую сторону. Если E_кин меньше U – частица вкатится только на часть «склона горки» и покатится назад, то есть она отразится от барьера.

Потенциальный барьер может соответствовать любому другому виду потенциальной энергии (например, потенциальный барьер, образованный комбинацией полупроводников с разной запрещенной зоной (рис. 1.3 а)). Электроны, находящиеся слева от барьера, имеют энергию, недостаточную для его преодоления. Внутрь полупроводника 2 эти электроны попасть не могут, поскольку значения их энергий внутри барьера запрещены – они попадают в запрещенную зону. Несмотря на это, в случае если размер барьера составляет несколько атомных слоев, часть потока электронов способна проникнуть за барьер. Данный эффект получил название туннелирования – прохождение электрона как бы сквозь туннель в барьере.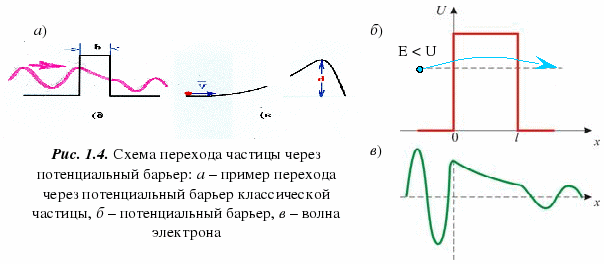



Эффект туннелирования имеет исключительно квантовую природу и связан с волновыми свойствами электрона. Чем «тоньше» барьер геометрически и чем меньше разность между высотой барьера U и E_кин квантовой частицы, тем больше шансов у электрона пройти этот барьер. В соответствии с гипотезой де Бройля частице с массой m и скоростью v соответствует длина волны λ₀ = 2πħ/mυ. Например, для электрона, имеющего скорость 10⁶ м/с (такую скорость он приобретет в вакууме за счет разности потенциалов в 3 В) λ₀ составит несколько межатомных расстояний. Если ширина барьера d меньше или равна λ₀, то случай перехода частицы через барьер становится возможным.

Туннельный эффект в интересующем нас простейшем случае означает следующее. Если квантовая частица находится по одну сторону потенциального барьера U, то существует возможность ее проникновения по другую сторону барьера, даже если ее полная энергия меньше U. Туннелирование, волновые свойства частиц, спин и квантование уровней энергии – все это проявления квантовой природы.

Интересно, что квантование уровней энергии происходит не только в атоме, но и в квантовых ямах (рис. 1.3 б) в том случае, если их размер составляет несколько атомных слоев. Видно, что движение электрона внутри ямы ограничено справа и слева, поскольку значения его энергии запрещены в этих областях. Если стенки ямы будут очень высокими, внутри ямы смогут существовать только стоячие волны, т.е. когда в яме будет укладываться только целое число полуволн: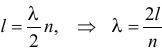



Вспоминая, что импульс и волна де Бройля связаны соотношением 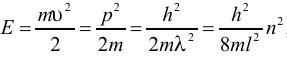, можно найти разрешенные энергии в квантовой яме:



где p – импульс электрона, m – его масса, h – постоянная Планка.

Поскольку электрон стремится занять минимальное энергетическое положение, он будет находиться на нижнем уровне и самостоятельно не сможет выбраться из ямы. Такой процесс называют захватом электрона или блокадой. Чтобы электрон освободился, ему необходимо передать энергию, равную разности переходов энергий в яме, например, в виде кванта света. И, наоборот, при протекании тока через такую систему электроны будут излучать кванты света только с длинами волн, строго определенными переходами между уровнями энергий. На этом эффекте построены большинство современных полупроводниковых диодов и лазеров.

Геометрически квантовая яма представляет собой структуру «сандвича», т.е. совмещенную структуру трех плоскостей из разных полупроводниковых материалов. Ограничение движения электрона в этом случае происходит только в направлении, перпендикулярном плоскостям. В двух остальных направлениях ограничение движения отсутствует, и электроны вдоль плоскостей двигаются свободно. Похожая картина наблюдается в квантовых нитях и квантовых точках (рис. 1.5). В квантовых нитях движение электронов ограничено в направлениях, перпендикулярных направлению нити. Вдоль нити электроны движутся свободно. В квантовой точке ограничение движения существует во всех направлениях. Электроны как бы заперты в такой структуре. Если квантовую точку зарядить отрицательно, то при отсутствии внешних воздействий этот заряд будет сохраняться сколько угодно долго. Такие структуры предполагается использовать для элементов полупроводниковой памяти в будущих сверхбыстродействующих компьютерах. Разнообразие наноматериалов огромно, поскольку сочетание нескольких материалов с известными свойствами в одной структуре может привести к появлению новых свойств. Поэтому свойства наноматериалов во многом определяются их структурой и возникающими вследствие этого квантовыми ограничениями. Как раз способам получения наноматериалов, их свойствам и областям применения посвящена следующая глава.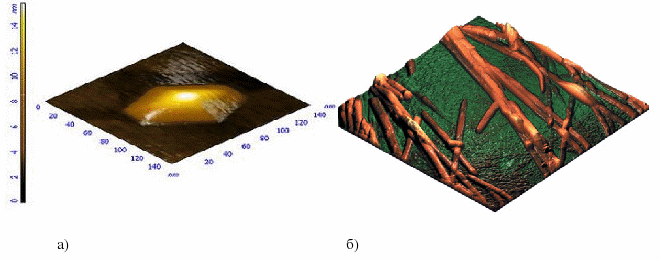



Рис. 1.5. Примеры квантовых нитей и квантовых точек:
а) Квантовая точка InAs, полученная на подложке InP. Размер изображения (140 x 140) нм;
б) Квантовые нити, полученные реакцией метилфосфорной кислоты, этанола и алюминия. Размер изображения (8 x 8) мкм