План лекц.. Строение вещества. I. Строение атома

• Название: Строение вещества. I. Строение атома
• Анкор: План лекц..doc
• Дата: 11.01.2018
• Размер: 14.08 Mb.
• Имя файла: План лекц..doc
• Тип: Документы; #13867
• страница: 1 из 17

Тема лекций №№ 13,14: Строение вещества.

I. Строение атома.

Вопросы:

1. Доквантовые модели атома (Томсона, Резерфорда, Бора).

2. Современные теории строения атома:

- протонно-нейтронная,

- квантово-механическая.

3. Радиоактивность: понятие, виды, характеристики.

4. Закономерности заполнения электронных орбиталей атомов.

Электронные схема, формулы.
Самостятельная работа:

1. Первые (до Томсона) модели атома.

2. Спектры испусканния электронов в полупроводниках, светодиоды.

3. Радиоактивность: понятие, виды, характеристики.

I. Строение атома
1. Доквантовые модели атома (Томсона, Резерфорда, Бора).

2. Протонно-нейтронная теория строения атома.
N(⁺¹₁p) = N_{порядковый}(хим. элемента)

m(⁺¹₁p) + m(⁰₁n) = m (атома), N(⁺¹₁p) + N(⁰₁n) = A_r(атома)
Таблица 1. Характеристики основных элементарных частиц атома
Элементарная ч-ца Абс.масса, кг Отн. масса, а.е.м. Электр.заряд, Кл Отн.заряд

Протон (⁺¹₁Р) 1,673^. 10^-27 1,0073 + 1,602^.10^-19 +1

Нейтрон ( ⁰₁n) 1,675^.10^-27 1,0087 0 0

Электрон (е^-) 9,109^.10^-31 0,00055 - 1,602^.10^-19 -1

2. Квантово-механическаятеория строения атома.

2.1. Три основополагающие идеи (положения) квантовой механики:

1. Квантование энергии электронов в атоме – принцип дискретности физических величин в микромире (микроявлений и микрообъектов), т.е. физические величины могут изменяться не непрерывно, а скачкообразно, принимая только определенные – дискретные значения.

О таких величинах говорят, что они квантуются.

Макс Планк (нем. физик,1900 г.):

тепловое излучение (абсолютно черного тела) состоит из дискретных порций – квантов энергии.

Значение одного кванта энергии ∆E = hν = E_ион + E_кин = E_ион + mv²/ 2.

h (постоянная Планка) – мера дискретности, которая как бы определяет границу между микро- и макромирами. Это одна из фундаментальнейших постоянных природы. Она входит во все квантово-механические соотношения (h = 6,626 ^.10 ^-34 Дж ^.с); ν = с/λ .
2. Двойственная природа (корпускулярно–волновой дуализм) электрона.

Луи де Бройль, фр. физик – квантовый механик, 1924 г.:

при своем движении электрон (е^-), как и др. частицы микромира (микрочастицы), обладает корпускулярно–волновойдвойственностью, т.е.

одновременно является и дискретной (отдельной) материальной частицей с массой покоя (m), зарядом (z), размерами, и волной, имея все ее свойства (дифракция, интерференция и др.).

Этот постулат выражается уравнением волны де Бройля: λ = h/ mv,

т.е.: частице, имеющей массу m и движущейся со скоростью v, соответствует волна длиной λ.

Постоянная Планка h связывает воедино корпускулярный и волновой характер движения материи.

В одних условиях на первый план выступают волновые свойства объектов, в других – корпускулярные, в третьих – те и другие одновременно. Свободный или связанный электрон нельзя назвать строго ни волной ни частицей. Электрон – это частица, если речь идет о дискретности, но это и волна, если обсуждается характер его движения.

Из уравнения де Бройля следует: чем меньше масса материальной частицы и больше ее скорость, тем характернее для нее волновые свойства.

Создать наглядную модель микрообъекта принципиально невозможно!
3. Принцип неопределенности Гейзенберга

(1927 г.):

(Вернер Гейзенберг, нем. физик - квантовый механик):

Для электрона, как для любой микрочастицы-волны, в принципе невозможно одновременно с одинаковой точностью измерить координату (местонахождение) и скорость движения (или импульс) - в любой момент времени.

Математическим выражением этого принципа является соотношение:

∆x = m ^.∆v > h / 2π,

где ∆x– неопределенность (погрешность измере-ния) положения электрона (любой микрочасти-цы) по оси ОХ,

∆v– неопределенность в измерении его скорос-ти (или импульса ∆р = m^.∆v).

Чем меньше значение ∆x, т.е. чем точнее определяем положение микрообъекта (в частности, электрона), тем больше неопределенность (ошибка) в определении значения его скорости или импульса, и наоборот.
2.2. Основные особенности квантового состояния электрона и электронной структуры атомов.
Движение (состояние) электрона в поле ядер атомов описывают с помощью волн де Бройля, которые в трехмерной, пространственной, системе координат математически отображаются волновой функцией Ψ(x, y, z). Волновые функции Ψ(x, y, z), «пси-функции», функции пространственных координат электрона – это разрешенные квантовые состояния электронов, определяющие энергетические уровни в атомеи области наиболее вероятного нахождения электронов в трехмерном пространстве вокруг атомного ядра.

Иначе (образно) волновую функцию Ψ(x, y, z) можно представитькак амплитуду 3-х-мерной электронной волны, точнее – амплитуды колебания вероятного присутствия электрона в данной области пространства. Другими словами, колеблется не сам электрон, а вероятность его обнаружения в данной области атомного пространства.

Движение электрона в атоме носит вероятностный характер – этоодин из постулатов квантовой механики, квантовой химии.

Наиболее вероятное квантовое состояние электрона – область околоядерного пространства, в котором электрон может находиться в разные моменты времени с максимальной вероятностью (до 98%),– называют атомной электронной орбиталью(АО) или «электронным облаком» -

совокупностью различных положений быстро движущегося электрона.

Математически АО представляют

как Ψ ²(x, y, z)^.∆V, т.е. как произведение квадрата волновой функции Ψ ²(x, y, z) – плотности вероятности - на элементарный объем атомного пространства ∆V.

Волновое уравнение Шредингера (1926 г.):

Эрвин Шредингер, австр. физик, предложил уравнение, связывающее энергию одноэлектронного атома водорода с его пространственными координатами (x, y, z) и волновой функцией Ψ(x, y, z),соответствующейамплитуде трехмерного волнового процесса:

[δ² Ψ(x)/ δx +δ²Ψ(Y)/δY² +δ²Ψ(Z)/δZ²] =

= -4 πm/ h [(E_полн – E_потенц) Ψ(x, y, z)].

Уравнение Шредингера строго не выводится (скорее постулируется, исходя из уравнения двумерной волны де Бройля). Тем не менее оно описывает реальное поведение (состояние) электрона в атоме и позволяет с большой точностью рассчитывать вероятность нахождения электрона в данный момент времени в любой точке пространства, занимаемого атомом.
Квантовые числа

Решения (корни) уравнения Шредингера содержат постоянные n, l, m_l , которые назвали квантовыми числами. Это квантовые дискретные характеристики волновой функции Ψ(x, y, z), описывающие силовое поле околоядерного пространства, в котором может находиться электрон, т. е. его энергетические уровни, подуровни и атомные орбитали.

Любое устойчивое состояние электрона в атоме характеризуют определенными значениями 4-х квантовых чисел: n(главное), l(орбитальное), m_l (магнитное),m_s (спиновое).

Каждой АО, т.е. наиболее вероятному квантовому состоянию электрона, соответствует свой набор указанных квантовых чисел.

Главное квантовое число nопределяет:

а) уровень электронной энергии атомной орбитали и атома, если этот уровень является внешним, наиболее удаленным от ядра;

б) номер (расстояние от ядра) данного квантового (энергетического) уровня и атомной орбитали. Квантовое числоnпринимает значения целых чисел, начиная с единицы:n = 1,2,3,…,∞;

в) максимально возможное число электронов N(е) на энергетическом уровне:N(е) = 2n².В атоме на уровне n = 1, например. может быть не более двух электронов,на уровне n = 2 –восьми, наn = 3 – восемнадцати электронов и т.д.

Орбитальное квантовое число lпринимает значения целых чисел от 0до (n – 1), характеризуя:

а) энергию электронов на подуровне, при этом число n здесь соответствует номеру квантового уровня, на котором впервыепоявляется этот подуровень;

б) форму электронной орбитали, АО:

s–АО (l = 0) имеет форму сферы,

р-АО(l = 1) – форму объемной восьмерки (гантели);

d-АО (l = 2) имеет форму четырех объемных лепестков (двух гантелей); f-AO (l = 3) – еще более сложную форму (8 гантелей и других).

Магнитное квантовое числоm_l характеризует магнитный момент электрона при движении по АО и пространственную ориентацию АО, принимая значения: m_l= 0, ±1, ±2,…, ±l.

Для каждого значения l, таким образом, разрешено (2l +1) значений m_l.

Все орбитали одного подуровня (n, l = const) имеют одинаковую энергию (энергетически вырождены), но по-разному ориентированы в пространстве магнитного поля ядра относительно друг друга.
(рис. Электронные облака)
Спиновое квантовое число m_s электрона имеет два значения, ±1/2, характеризуя собственный магнитный момент количества движения электрона вокруг ядра атома при одновременном вращении вокруг своей оси в двух взаимно противоположных направлениях.

Атомные орбитали, для которых значения l= 0, 1, 2, 3, называют соответственно s-, p-, d-, f-АО. Так же называют и энергетические подуровни:

s-, p-, d-, f- подуровни, включающие 1, 3, 5 и 7 соответствующих АО, и химические элементы, образующие s-, p-, d-, f- электронные семейства, в атомах которых валентные электроны заполняют соответствующие подуровни.

Например, квантовому состоянию электрона 3s² (второй электрон на 3s –АО)отвечает набор квантовых чисел: n = 3, l = 0, m_l= 0, m_s = - ½.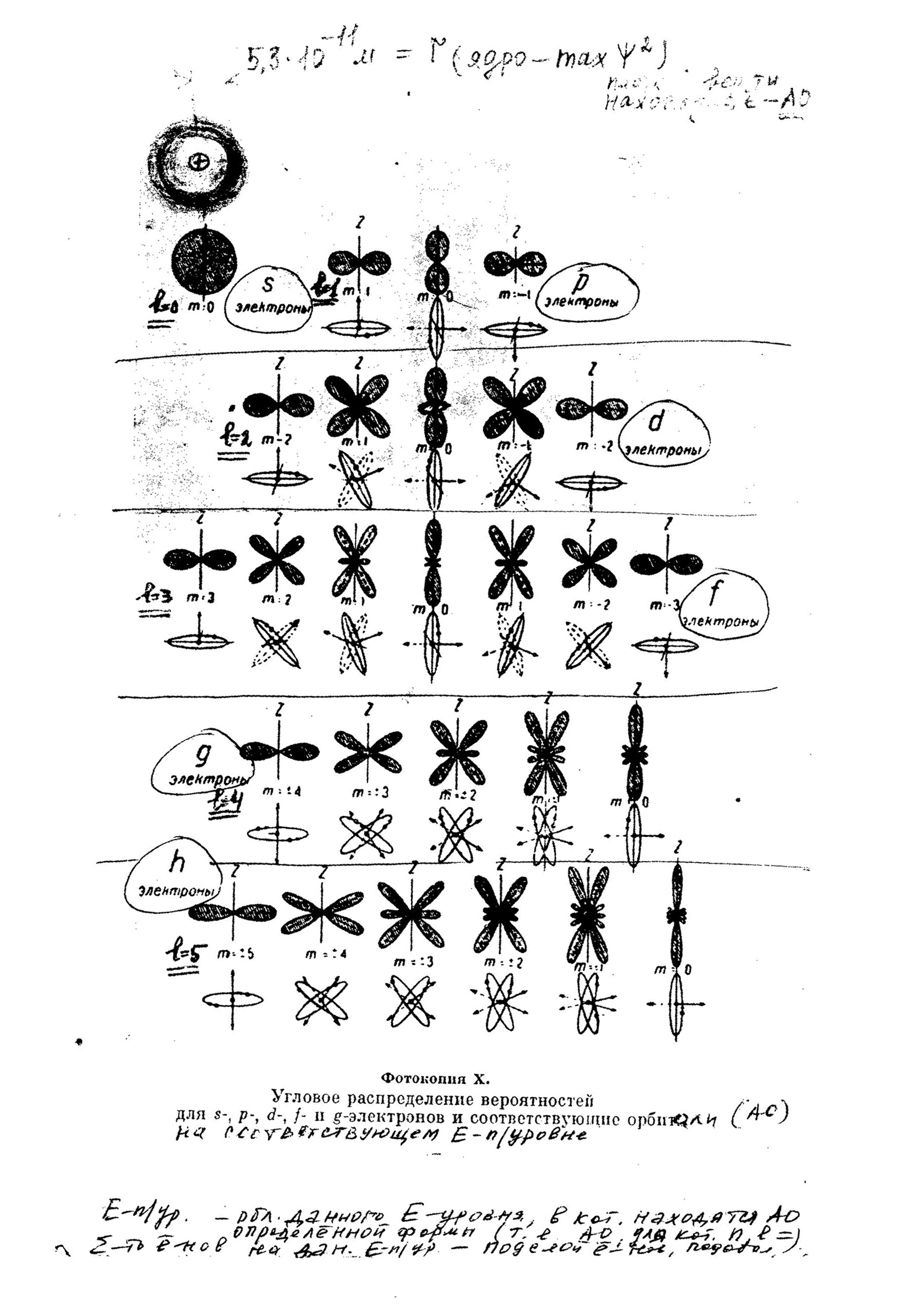



Заполнение энергетических уровней, подуровней и атомных орбиталей подчиняется четырем основным правилам и принципам:
1. Принцип Паули:

в атоме не может быть даже двух электронов с одинаковым набором 4-х квантовых чисел.

Из этого следует, что каждая АОможет быть занята не более чем двумя электронамис разными по знаку спиновыми квантовыми числами m_s, равными+ ½. Такие два электрона называют спареннымиилиантипараллельными

(с антипараллельными спинами).
2. Принцип минимальной энергии:

устойчивому (невозбужденному) состоянию атома отвечает такое расположение электронов по АО, при котором энергия атома минимальна; АО заполняются в порядке последовательного возрастания их энергий, начиная с первого энергетического (квантового) уровня, n = 1.

3. Правило Клечковского

(иначе - «минимального (n + l)») –

определяет порядок заполнения электронами АО многоэлектронного атома:

заполнение энергетических уровней и подуровней многоэлектронного атома, находящегося в основном (невозбужденном) состоянии, происходит в порядке увеличения суммы главного и орбитального квантовых чисел (n + l), а при равных значениях (n + l) – в порядке возрастания n.

Не забываем при этом, что каждому типу подуровня всегда соответствует единственное значение орбитального квантового числа l:

l_s-АО = 0, l_р-АО = 1, l_d-АО = 2, l_f-АО = 3.

Исключения из правила Клечковского - так называемые «провалы электронов»с ns- на (n-1) d-АО -

у атомов d-металлов: Cr, Cu, Ag, Au, Mo, Ru, Rh, Pd, Pt - связаны с повышенной устойчивостью атомов в таких состояниях их валентных электронов, когда они заполняют d-подуровень либо наполовину (5 неспаренных электроновс параллельными спинами), либо полностью (10 электронов, т.е. 5 пар электронов с антипараллельными спинами). В свободном атоме d-АО являются большими по размерам и размытыми в пространстве. Когда они заселены электронами наполовину или полностью, то размеры их меньше, орбитали сжаты в пространстве и, как показывают квантово-механические расчеты, их энергия меньше и, значит, выше устойчивость.

4. Правило Гунда («максимального спина»,

которому подчиняется размещение электронов на АО энергетического подуровня: