ФОЭ2A. Статистика носителей заряда в полупроводниках глава 2

• Название: Статистика носителей заряда в полупроводниках глава 2
• Дата: 14.11.2022
• Размер: 0.99 Mb.
• Имя файла: ФОЭ2A.doc
• Тип: Глава; #788133
• страница: 1 из 7

Глава 2. Статистика носителей заряда в полупроводниках

Г Л А В А 2

СТАТИСТИКА НОСИТЕЛЕЙ ЗАРЯДА

В ПОЛУПРОВОДНИКАХ

(равновесные концентрации носителей заряда, распределение по энергии генерация и рекомбинация носителей заряда, влияние поверхностных состояний)

2.1. Расчет концентрации электронов и дырок в собственном полупроводнике

Величина концентрации свободных электронов n_iв зоне проводимости собственного проводника раccчитывается путем интегрирования соотношения типа (1.13):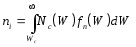

, (2.1)

где W_c - энергия дна зоны проводимости; N_c(W) - плотность состояний энергии электронов в зоне проводимости, которая рассчитывается из выражения (1.7); f_n(W) - функция Ферми-Дирака распределения электронов по энергиям, определяемая соотношением (1.10).

На рис. 2.1 изображены графики функций Ферми-Дирака для электронов и дырок при температуре T>0, совмещенные с энергетической зонной диаграммой полупроводникового материала.

В диапазоне энергий, соответствующем дну зоны проводимости W_c ("хвост" функции распределения на рис. 2.1, а), величина [(W-W_F)/kT]>> 1. Поэтому функция распределения электронов по энергиям (1.10) при температуре Т>0 приближенно описывается распределением Максвелла-Больцмана, имеющим вид

, (2.2)

где W_F - значение энергии, соответствующее уровню Ферми в полупроводнике.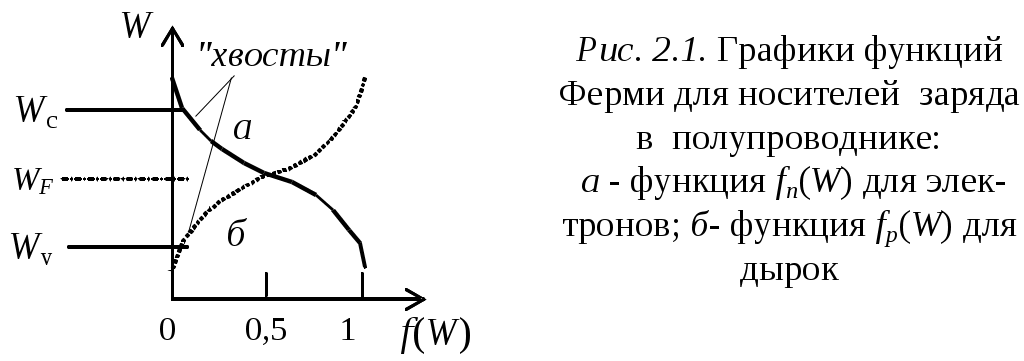



Подставляя в формулу (2.1) значения N_c(W) из выражения (1.7) и f_n(W) из формулы (2.2), получим следующее соотношение для расчета концентрации электронов в зоне проводимости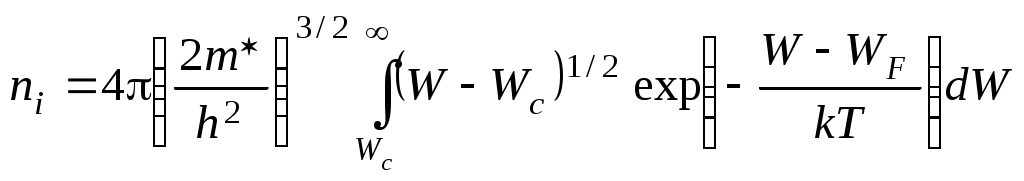

. (2.3)

Умножив и разделив правую часть полученного соотношения на (kT)^3/2, преобразуем его к виду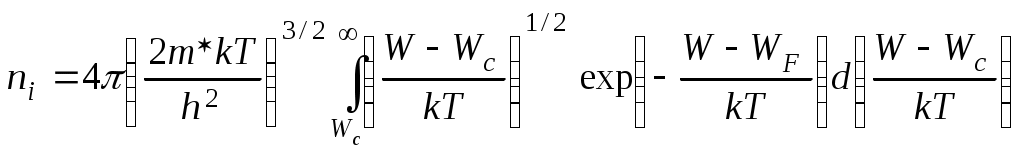

.

Обозначим , .

Тогда , а пределы интегрирования по переменной x будут находиться в диапазоне . В результате интеграл для расчета значения n_i преобразуется к виду

. (2.4)

В этой формуле - интеграл Ферми половинного порядка. Подставляя значение интеграла Ферми в формулу (2.4) получим, что концентрация электронов в собственном полупроводнике определяется выражением

. (2.5)

В выражении (2.5) обозначим , м^-3. Величина N_c носит название эффективной плотности состояний в зоне проводимости и для кремния при Т=300 К составляет 2,810²⁵ м^-3. Производя подстановку N_c в выражение (2.5) получим окончательное выражение для концентрации электронов в собственном полупроводнике в виде

. (2.6)

Используя полученные результаты рассчитаем концентрацию дырок, p_i в валентной зоне собственного полупроводника. В данном случае для расчетов используем выражение, аналогичное выражению (2.1):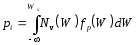

, (2.7)

где W_v - энергия потолка валентной зоны; N_v(W) - плотность состояний энергии электронов в валентной зоне, которая рассчитывается из выражения, аналогичного (1.7); f_p(W) – функция Ферми-Дирака распределения дырок по энергиям.

Интегрирование в формуле (2.7) идет в пределах от до W_v.

График функции f_p(W) для Т>0 представлен на рис. 2.4, б. Согласно этому графику функция Ферми-Дирака для дырок является дополнительной к функции Ферми-Дирака для электронов f_n(W), т. е.

f_p(W)=1 ̶f_n(W)= . (2.8)

В диапазоне энергий, соответствующем потолку валентной зоны W_v ("хвост" функции распределения на рис. 2.1, б), величина [-(W-W_F)/kT]>>1. Поэтому функция распределения дырок по энергиям (2.13) при температуре Т 0 приближенно описывается распределением Максвелла-Больцмана, имеющим в данном случае вид

, (2.9)

где W_F - значение энергии, соответствующее уровню Ферми в полупроводнике.

Подставляя в формулу (2.7) значение N_v(W) из формулы (1.7), в которой эффективная масса электронов заменена на эффективную массу дырок 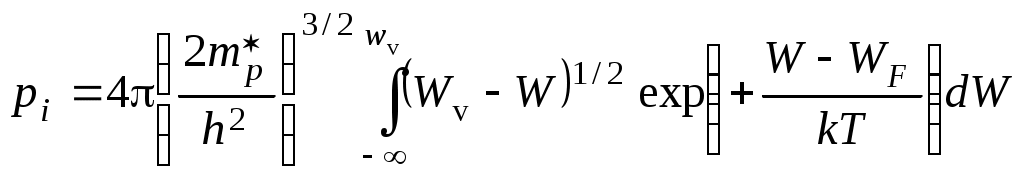и отсчет энергии идет вниз от потолка валентной зоны W_v, а также значение f_p(W) из выражения (2.9), получим следующее рабочее соотношение для расчета концентрации дырок в валентной зоне:
. (2.10)

Выполняя преобразования формулы (2.15) по аналогии с проведенным выше при расчетах концентрации электронов, получим, что концентрация дырок в собственном полупроводнике определяется выражением

(2.11)

где ; м^-3 - эффективная плотность состояний в валентной зоне, равная для кремния 1,010²⁵ м^-3 при Т= 300 К.

Производя подстановку N_v в выражение (2.11) получим выражение для концентрации дырок в собственном полупроводнике:

. (2.12)

В собственном полупроводнике концентрации свободных электронов и дырок связаны законом равновесия масс (1.4), откуда следует, что эти концентрации равны между собой и определяются соотношением вида

, м^-3. (2.13)

Подставляя значения n_i из(2.6) и p_iиз (2.12) в соотношение (2.13), получим следующую формулу для расчета концентрации электронов и дырок в собственном полупроводнике:

.

Поскольку разность W_c – W_v равна W_g - ширине запрещенной зоны полупроводника, то выражение для концентрации носителей заряда в собственном полупроводнике может быть записано в виде

. (2.14)

Из выражения (2.14) следует, что в собственном полупроводнике при фиксированной температуре Т концентрация электронов n_i,(и дырок p_i) тем выше, чем меньше ширина запрещенной зоны полупроводника W_g и чем больше эффективные плотности состояний в зоне проводимости N_c и в валентной зоне N_v. С ростом температуры Т значения концентраций собственных носителей заряда n_i и p_i возрастают.